Методы экспертного анализа

Лабораторная работа № 10

«Принятие оптимальных решений при многих критериях»

(4 часа)

Цель работы: ознакомится с методами экспертного анализа.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Особенности многокритериальной оптимизации

Как правило, на практике решения принимаются с учетом нескольких критериев (вектора критериев). Такие задачи называются многокритериальными, или задачами векторной оптимизации. Отметим основные проблемы, возникающие при многокритериальной оптимизации.

1) Противоречивость критериев. Как правило, улучшение по одному критерию приводит к ухудшению по другому критерию. Например, более производительный компьютер стоит дороже.

2) Наличие разнородных оценок: числовые, качественные («быстрый» процессор, «отличная машина» и т.п.), оценки вида «да – нет», балльные оценки, оценки в виде ранжирования и т.д., которые к тому же отличаются по размерности (например, цена – в рублях, производительность компьютера – в миллионах операций в секунду, объем оперативной памяти – в гигабайтах и т.п.).

3) Критерии могут сильно различаться по важности.

4) Крайне сложно (а иногда и невозможно) определить аналитическую зависимость между критериями.

Существуют различные способы решения этих проблем в процессе принятия решения. Одним из основных способов, который используется в большинстве методов решения многокритериальных задач, является приведение оценок по различным критериям к единой форме и получения обобщенной оценки альтернативы. Рассмотрим основные способы приведения оценок.

1) Перевод качественных оценок в числовую форму осуществляется по шкале Харрингтона (таблица 1).

Таблица 1 – Шкала Харрингтона

В случае, если две альтернативы имеют одинаковую оценку «хорошо», но по мнению эксперта вторая альтернатива лучше, то первой альтернативе можно назначить оценку 0,7, а второй – 0,8.

Для оценок, имеющих вид «да – нет», используют следующую шкалу: «да» – 0,67; оценки вида «нет» – 0,33.

2) Оценки различного рода, представленные различными системами измерений, заменяются экспертными оценками, представленными в виде балльных оценок, в долях единицы, в виде парных сравнений, в виде ранжирования и т.д.

3) Нормирование критериев. Числовые оценки из произвольного диапазона приводят к единому масштабу, то есть оценкам, лежащим в диапазоне [0;1]. При этом, как правило, лучшей оценке соответствует большее значение:

,

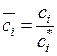где 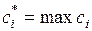, , n – число критериев.

Также может использоваться безразмерная оценка, характеризующая отклонения от оптимальных значений критериев:

.

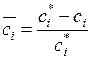Для упрощения задачи несколько критериев могут быть заменены одним обобщенным критерием

,

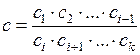где 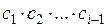– критерии, которые необходимо увеличить, 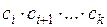– критерии, которые необходимо уменьшить, n – число критериев.

Для этой же цели может быть использован обобщенный критерий в виде взвешенной суммы отдельных критериев:

,

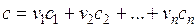где 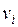– вес i -го критерия, 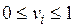, , n – число критериев.

Методы экспертного анализа