Лекция 7
Силовой анализ механизмов аналитическим методом
Силовой расчет заключается в определении сил, действующих на звенья механизма, при известном законе движения начального звена. Силовой расчет является первой (прямой) задачей динамики.
Задачи силового расчета
1. Определение сил приложенных к звеньям механизма. Эти силы необходимы для расчета звеньев на прочность и жесткость.
2. Определение сил реакций в кинематических парах (КП). Значения полученных реакций используют для выбора типов и размеров подшипников из условия долговечности, вычисления коэффициента полезного действия механизма.
3. Определение уравновешивающего (или движущего) момента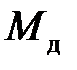 
, через который определяют мощность машины
,
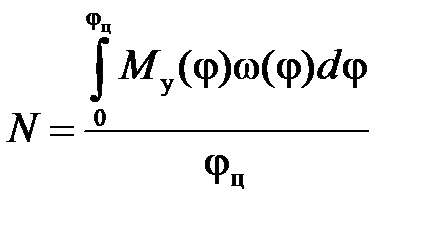где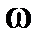 
–угловая скорость начального звена.
Допущения, принимаемые при силовом расчете плоских рычажных механизмов
1. Силы трения не учитываются.
2. Звенья считаются абсолютно твердыми телами.
3. Все силы действуют в одной плоскости.
4. Все звенья имеют плоскость симметрии, совпадающую с плоскостью движения.
Метод расчета
Для силового расчета обычно применяют принцип Д’Аламбера. Силовой расчет с применением этого принципа называют кинетостатическим.
Принцип Д’Аламбера.
Если в любой момент времени к каждой точке системы кроме действующих на нее внешних и внутренних сил присоединить силы инерции, то полученная система сил будет уравновешенной и к ней можно применить уравнения равновесия.
Звено является абсолютно твердым телом, к каждой точке которого приложена элементарная сила инерции. Элементарные силы инерции всех точек звена приводят к центру масс и заменяют главным вектором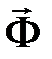 
и главным моментом 
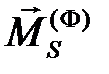сил инерции.
При плоскопараллельном движении звена главный вектор и главный момент сил инерции определяют по следующим формулам:
,
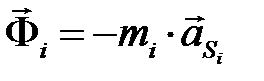где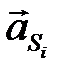 
– ускорение центра масс звена i; 
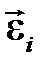– вектор углового ускорения; звена; 
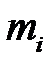– масса звена; 
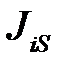– момент инерции звена относительно оси, проходящей через центр масс и перпендикулярной плоскости движения.
При поступательном движении звена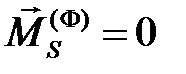 
,а при вращательном движении звена, у которого центр масс расположен на оси вращения – 
.
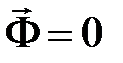При аналитическом расчете плоских механизмов главный вектор сил инерции раскладывают по осям координат
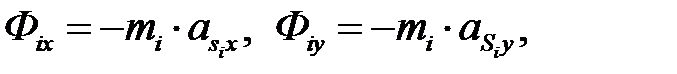
а главный момент сил инерции определяют по формуле
,
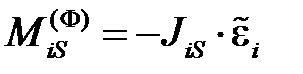где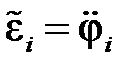 
– алгебраическое значение углового ускорения звена i.
Обычно применяют следующее правило знаков: если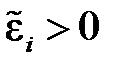 
,то оно направлено против часовой стрелки, в противном случае –по часовой стрелке.Для главного момента сил инерции 
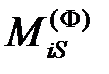применяют аналогичное правило. На расчетной схеме 
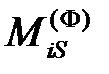направляют в положительную сторону против часовой стрелки.
Уравнения равновесия звена с учетом сил инерции, называемые уравнениями кинетостатики, имею вид
,
где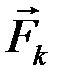 
- внешние силы, действующие на звено i.
При аналитическом выполнении расчетов с использованием ЭВМ моменты сил удобно вычислять относительно начала координат (т. O) по формуле:
,
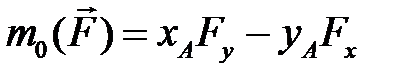где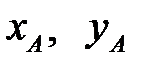 
– координаты точки приложения силы 
.
Реакции в кинематических парах
Силы взаимодействия звеньев (реакции в КП) обозначаютс двойным нижним индексом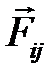 
. Первая цифра индекса указывает на звено, к которому приложена сила, вторая цифра – звено, со стороны которого действует сила. Например, 
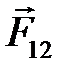–сила, с которой звено 2 действует на звено 1.
Рассмотрим реакции в кинематических парах, пренебрегая силами трения.
Вращательная КП.
Сила реакцииво вращательной КП лежит в плоскости относительного движения звеньев. Модуль и направление реакции зависит от сил, действующих на звено, и определяются в результате силового расчета. При выполнении силового расчета аналитическим методом реакции во вращательных КП раскладывают на две составляющие по осям координат(рис. 7.1).
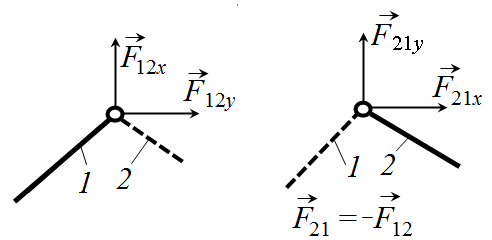
Рис.7.1. Реакция во вращательной КП
На расчетных схемах показывают положительные направления сил. По 3 закону Ньютона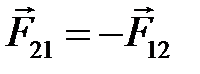 
. Следовательно, 
.
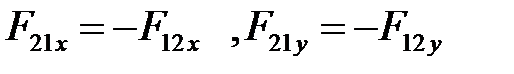Во вращательной кинематической паре необходимо определять две неизвестные величины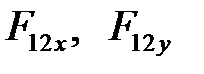 
.
Поступательная КП.
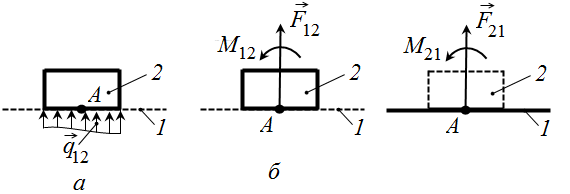В поступательной КП реакция является распределенной силой 
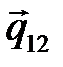(рис. 7.2, а), которая направлена перпендикулярно направляющей. Распределенную силу реакции 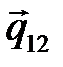при приведении к произвольной точке A заменяют главным вектором 
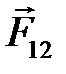и главным моментом 
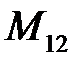(рис. 7.2 б). Главный вектор 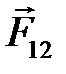приложен к точке приведения (т. A) и направлен перпендикулярно направляющей. Положительное направление 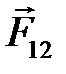задают произвольно, положительное направление момента 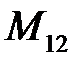– против часовой стрелки. На расчетной схеме 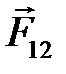, 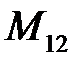направляют в положительную сторону. Истинные направления определяют в результате силового расчета. При составлении уравнений равновесия учитывают, что по 3 закону Ньютона 
.
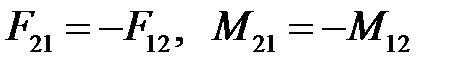Рис. 7.2. Реакция в поступательной КП:
а – распределенная сила реакции 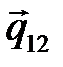; б – главный вектор и главный момент распределенной реакции
Если главный вектор 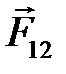не равен нулю, то распределенную реакцию 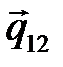можно эквивалентно заменить равнодействующей силой 
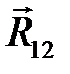(рис. 7.3). В этом случае величину равнодействующей 
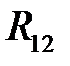и точку её приложения (плечо 
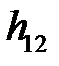) определяют из уравнений кинетостатики.
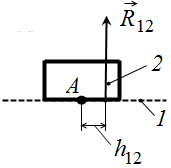
Рис.7.3. Равнодействующая распределенной реакции в поступательной КП
Следовательно, в поступательной паре КП необходимо определять две неизвестные величины 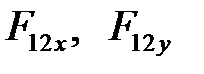(или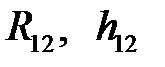 
).
Примечание. Если точка приложения равнодействующей расположена вне поверхности соприкосновения звеньев, то на звено действуют две сосредоточенные силы, приложенные на границах поверхности соприкосновения (рис. 7.4). При этом
, 
.
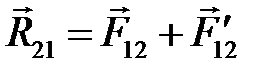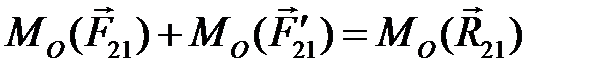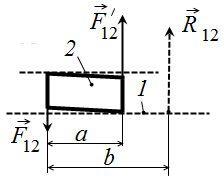
Рис. 7.4.
Высшая кинематическая пара.
В высшей кинематической пареконтакт звеньев может происходить по линии или в точке. При точечном контакте сила реакции является сосредоточенной, при линейном контакте – распределенной по линии.
В высшей КП реакция направлена вдоль общей нормали (n-n), проведенной в точке касания (т. A)к двум соприкасающимся поверхностям 1 и 2 (рис. 7.5).
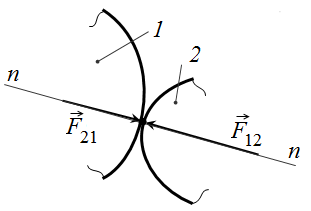
Рис. 7.5 Реакция в высшей кинематической паре
В высшей кинематической паре на плоскости необходимо определять одну неизвестную величину – модуль реакции.