Свойства параллельных плоскостей

Стереометрия

Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве. Слово «стереометрия» происходит от греческих слов «стереос» - объёмный, пространственный и «метрео» - измерять.

Основными фигурами в пространстве являются точка, прямая и плоскость.

Кроме этих фигур мы будем рассматривать геометрические тела и их поверхности.

Геометрические тела

1) Многогранники: призма, параллелепипед, пирамида и др;

2) Тела вращения: цилиндр, конус, шар и др.

Аксиомы стереометрии

А(Ст)1. Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей. Краткая запись:
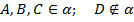
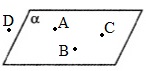
А(Ст)2. Если две разные плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку. Краткая запись:
А(Ст)3. Если две разные прямые имеют общую точку, то через них можно провести плоскость, и притом единственную. Краткая запись:
А(Ст)4. Для произвольной плоскости выполняются аксиомы планиметрии.

Теоремы взаимосвязи точек, прямых и плоскости

Т1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.   (самостоятельно сделать краткую запись)
Т2. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.   (самостоятельно сделать краткую запись)   Следствие Т2. Плоскость и не лежащая на ней прямая либо не пересекаются, либо пересекаются в одной точке.   (самостоятельно сделать краткую запись)
Т3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.   (самостоятельно сделать краткую запись)
Т4. Плоскость разбивает пространства на два полупространства. Если точки Х и У принадлежат одному полупространству, то отрезок ХУ не пересекает плоскость. Если же точки Х и У принадлежат разным полупространствам, то отрезок ХУ пересекает плоскость.	Рисунок и краткую запись выполняют учащиеся самостоятельно.

Возможны три случая взаимного расположения прямой и плоскости:

а) прямая лежит а плоскости;

б) прямая и плоскость имеют одну общую точку (т.е. они пересекаются);

в) прямая и плоскость не имеют ни одной общей точки (т.е. они параллельны).

Теоремы параллельности прямых и плоскостей

Т5. Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну.   (самостоятельно сделать краткую запись)
Т6. Две прямые, параллельные третьей прямой, параллельны между собой.   (самостоятельно сделать краткую запись)
Т7. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.   (самостоятельно сделать краткую запись)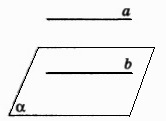
Т8. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.   (самостоятельно сделать краткую запись)
Т9. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.     (самостоятельно сделать краткую запись)

Свойства параллельных плоскостей

С1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны между собой.     (самостоятельно сделать краткую запись)
С2. Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны.     (самостоятельно сделать краткую запись)