1. Основные понятия о числовых рядах и определения.
Числовой последовательностью называется упорядоченный набор нумерованных чисел  , представляющая собой функцию
, представляющая собой функцию
 ,
,  (1)
(1)
заданную на множестве натуральных чисел. Числа 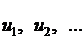 называются соответственно первым, вторым и так далее членами последовательности. Число
называются соответственно первым, вторым и так далее членами последовательности. Число  , задаваемое формулой (1), называется общим членом последовательности.
, задаваемое формулой (1), называется общим членом последовательности.
В последовательностях и рядах широко используется функция натурального аргумента
 ,
,
представляющая собой произведение первых  натуральных чисел. Обозначение
натуральных чисел. Обозначение  читается как «эн факториал».
читается как «эн факториал».
Пусть u1, u2, u3,…, un,…, где un = f(n), - бесконечная числовая последовательность. Тогда выражение

| (2) |
называется числовым рядом.
Числа 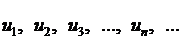 называются членами ряда. При этом
называются членами ряда. При этом
 , , 
|
называется общим членом ряда. Ряд считается заданным, если задана формула для  . Нумерация членов ряда, вообще говоря, может начинаться с любого целого числа.
. Нумерация членов ряда, вообще говоря, может начинаться с любого целого числа.
Сумму первых членов ряда по n -ный включительно обозначают Sn и называют n -ной частичной суммой ряда, т.е.

|
Сумму остальных слагаемых, начиная с  - го, называют n-ным остатком числового ряда и обозначают
- го, называют n-ным остатком числового ряда и обозначают  , т.е.
, т.е.

|
Согласно определению (2), остаток числового ряда можно рассматривать как самостоятельный числовой ряд.
Предел последовательности  частичных сумм при
частичных сумм при  , если он существует, называется суммой ряда и обозначается буквой S, т.е.
, если он существует, называется суммой ряда и обозначается буквой S, т.е.
 . .
|
Если  существует, т.е. если сумма S есть конечное число, то говорят, что ряд (2) сходится. В противном случае говорят, что ряд (2) расходится.
существует, т.е. если сумма S есть конечное число, то говорят, что ряд (2) сходится. В противном случае говорят, что ряд (2) расходится.
Частный случай числового ряда – геометрический ряд, представляющий собой сумму бесконечной геометрической прогрессии:
 . .
|
Его частичная сумма:
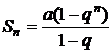 . .
|
При этом если  , то геометрическая прогрессия называется бесконечно убывающей, и геометрический ряд имеет конечную сумму
, то геометрическая прогрессия называется бесконечно убывающей, и геометрический ряд имеет конечную сумму
 . .
|
В случаях, когда  , геометрический ряд расходится, т.е. конечной суммы не имеет.
, геометрический ряд расходится, т.е. конечной суммы не имеет.
2. Свойства числовых рядов. Необходимый признак сходимости.
Свойство 1.
Если сходится ряд
 , ,
| (3) |
то сходится и ряд, полученный из данного отбрасыванием конечного числа его членов. Наоборот, если сходится ряд, полученный из данного путем отбрасывания конечного числа его членов, то сходится и данный ряд.
В частном случае, когда речь идет об отбрасывании первых членов ряда, свойство можно сформулировать так: если сходится ряд (3), то сходится и ряд
 , ,
|
и наоборот (m – конечное число первых отброшенных членов).
В более широком смысле данное свойство можно сформулировать следующим образом: отбрасывание или добавление конечного числа членов ряда не изменяет его сходимости или расходимости.
Свойство 2.
Если сходится ряд

|
и его сумма равна  , то сходится и ряд
, то сходится и ряд
 ,
,
где a – некоторое число, и сумма его равна  .
.
Свойство 3.
Если сходятся ряды
 и
и  ,
,
и их суммы равны соответственно  и
и  , то сходится и ряд
, то сходится и ряд
 ,
,
и сумма его равна  .
.
Необходимый признак сходимости.
Если ряд

сходится, то его общий член  при
при  стремится к нулю, т.е.
стремится к нулю, т.е.
 .
.
3. Достаточные признаки сходимости знакоположительных рядов.
Знакоположительным называется такой числовой ряд, все члены которого положительны.
Первый признак сравнения(признак сравнения в непредельной форме).
Пусть даны два ряда с положительными членами:
 (4)
(4)
и
 , (5)
, (5)
причем каждый член ряда (4) не превосходит соответствующего члена ряда (5), т.е.
 ,
, 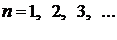 . (6)
. (6)
Тогда если сходится ряд (5), то сходится и ряд (4); если расходится ряд (4), то расходится и ряд (5).
Этот признак справедлив и для случая, когда условие (6) начинает выполняться не при  , а с любого значения номера
, а с любого значения номера  .
.
Второй признак сравнения(признак сравнения в предельной форме).
Пусть для рядов (4) и (5) существует предел
 .
.
Тогда если  , то либо оба ряда сходятся, либо оба ряда расходятся; если
, то либо оба ряда сходятся, либо оба ряда расходятся; если  и ряд (5) сходится, то сходится и ряд (4). Если же
и ряд (5) сходится, то сходится и ряд (4). Если же

и ряд (5) расходится, то расходится и ряд (4).
Ряды, сходимость или расходимость которых полезно запомнить для применения признаков сравнения.
Гармонический ряд: 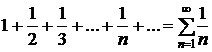 ; этот ряд расходится.
; этот ряд расходится.
Обобщенный гармонический ряд (или ряд Дирихле):  ; этот ряд расходится при
; этот ряд расходится при  и сходится при
и сходится при  . Рассмотренный выше гармонический ряд является частным случаем ряда Дирихле при
. Рассмотренный выше гармонический ряд является частным случаем ряда Дирихле при  .
.
Признак Даламбера.
Если для ряда с положительными членами

существует предел отношения последующего члена к предыдущему
 ,
,
то этот ряд сходится при  и расходится при
и расходится при  .
.
При  возможны оба случая, т.е. исследование такого ряда по признаку Даламбера не дает однозначного ответа на вопрос о сходимости.
возможны оба случая, т.е. исследование такого ряда по признаку Даламбера не дает однозначного ответа на вопрос о сходимости.
Радикальный признак Коши.
Если для ряда с положительными членами

существует предел
 ,
,
то этот ряд сходится, если  , и расходится, если
, и расходится, если  .
.
При  возможны оба случая, т.е. исследование такого ряда по радикальному признаку Коши не дает однозначного ответа на вопрос о сходимости.
возможны оба случая, т.е. исследование такого ряда по радикальному признаку Коши не дает однозначного ответа на вопрос о сходимости.
Интегральный признак Коши.
Ряд с положительными членами
 , (7)
, (7)
где 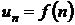 , и
, и  - непрерывная монотонно убывающая при
- непрерывная монотонно убывающая при  функция, сходится, если сходится несобственный интеграл
функция, сходится, если сходится несобственный интеграл
 . (8)
. (8)
Если же интеграл (8) расходится, то расходится и ряд (7).
4. Знакопеременные ряды. Абсолютная и условная сходимости.
Числовой ряд называется знакопеременным, если он содержит как положительные, так и отрицательные члены, причем количества и тех и других бесконечны.
Знакопеременный ряд
 , (9)
, (9)
сходится, если сходится ряд, составленный и модулей его членов:
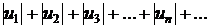 . (10)
. (10)
При этом говорят, что ряд (9) сходится абсолютно. Если же ряд (10) расходится, то ряд (9) может как сходиться, так и расходиться. В случае его сходимости говорят, что он сходится неабсолютно, или условно.
5. Знакочередующиеся ряды. Признак Лейбница.
Знакочередующиеся ряды представляют собой частный случай знакопеременных рядов, когда знаки членов «плюс» и «минус» поочередно меняются. Если считать все числа  положительными, то знакочередующийся ряд в общем виде можно записать таким образом:
положительными, то знакочередующийся ряд в общем виде можно записать таким образом:
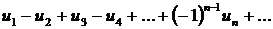 ,
,  (11)
(11)
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, и общий член ряда по модулю стремится к нулю.
Таким образом, для сходимости знакочередующегося ряда (11) достаточно выполнения двух условий:
1)  ;
;
2)  .
.
Следствия из теоремы Лейбница:
1) сумма сходящегося знакочередующегося ряда, записанного в форме (11), положительна и меньше его первого члена:
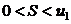 ; (12)
; (12)
2) если ряд (11) сходится по признаку Лейбница, то его остаток

по модулю меньше своего первого члена: 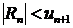 .
.
6. Функциональные ряды.
Функциональным называется ряд, члены которого суть функции переменной  :
:
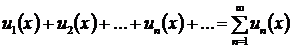 , (13)
, (13)
Функция

называется частичной суммой ряда (13). Предел частичной суммы при  , если он существует как функция аргумента
, если он существует как функция аргумента  , называется суммой функционального ряда:
, называется суммой функционального ряда:
 .
.
При этом говорят, что ряд (13) сходится. Значение  , при котором ряд (13) сходится, т.е. сходится числовой ряд
, при котором ряд (13) сходится, т.е. сходится числовой ряд  , называется точкой сходимости функционального ряда. Множество значений аргумента
, называется точкой сходимости функционального ряда. Множество значений аргумента  , при которых функции
, при которых функции  определены, и ряд
определены, и ряд 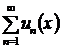 сходится, называется областью сходимости функционального ряда.
сходится, называется областью сходимости функционального ряда.
Функция

называется остатком функционального ряда.
7. Степенные ряды. Область и радиус сходимости степенного ряда.
Степенным рядом называется функциональный ряд вида
 , (14)
, (14)
где a, A0, A1, A2, …, An, … - действительные числа.Частный случай степенного ряда при  :
:
 .
.
Теорема Абеля. Если степенной ряд (14) сходится при  , то он сходится, причем абсолютно, при любом x, удовлетворяющем неравенству
, то он сходится, причем абсолютно, при любом x, удовлетворяющем неравенству
 . (15)
. (15)
Если же ряд (14) расходится при  , то он расходится и при любом x, удовлетворяющем неравенству
, то он расходится и при любом x, удовлетворяющем неравенству
 . (16)
. (16)
Поясним формулировку теоремы Абеля. После несложных преобразований условия (15) и (16) можно соответственно записать в виде
 ,
,
 .
.
Отсюда следует, что число  в окрестности точки a образует симметричный относительно нее интервал. При этом если ряд сходится при
в окрестности точки a образует симметричный относительно нее интервал. При этом если ряд сходится при  , то гарантирована его сходимость и внутри интервала. Если же он расходится при
, то гарантирована его сходимость и внутри интервала. Если же он расходится при  , то он обязательно расходится и во всех точках вне интервала. Таким образом, теорема Абеля фактически устанавливает существование симметричного относительно точки
, то он обязательно расходится и во всех точках вне интервала. Таким образом, теорема Абеля фактически устанавливает существование симметричного относительно точки  интервала абсолютной сходимости степенного ряда. Половина его длины обозначается R и называется радиусом сходимости, а точка
интервала абсолютной сходимости степенного ряда. Половина его длины обозначается R и называется радиусом сходимости, а точка  - центром сходимости.
- центром сходимости.
Радиус сходимости R может принимать значения от 0 до  , т.е.
, т.е.  . Интервал абсолютной сходимости может быть записан в виде
. Интервал абсолютной сходимости может быть записан в виде 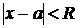 . Сходимость ряда в точках
. Сходимость ряда в точках  и
и  должна быть исследована особо, и в случае ее установления соответствующая граница добавляется к интервалу, образуя область сходимости.
должна быть исследована особо, и в случае ее установления соответствующая граница добавляется к интервалу, образуя область сходимости.
Применив к степенному ряду признак сходимости Даламбера, для радиуса сходимости можно получить формулу
 . (17)
. (17)
Эта формула справедлива только в тех случаях, когда ряд содержит все целые степени разности 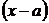 , т.е. не имеет нулевых коэффициентов.
, т.е. не имеет нулевых коэффициентов.
Если же для анализа сходимости степенного ряда применить радикальный признак Коши, то получится формула
 .
.
Теорема. Любой степенной ряд внутри его интервала сходимости можно почленно интегрировать и дифференцировать; при этом его радиус сходимости сохраняется, а сумма ряда также интегрируется или дифференцируется.
8. Ряды Тейлора и Маклорена.
Рядом Тейлора для функции  называется степенной ряд
называется степенной ряд
 . .
| (18) |
При этом говорят, что ряд Тейлора построен для  в точке
в точке 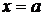 .
.
Остаток ряда Тейлора может быть записан в форме Лагранжа:
 , ,  . .
|
Если функция  бесконечно дифференцируема в некоторой области
бесконечно дифференцируема в некоторой области  и при этом в этой области выполняется условие
и при этом в этой области выполняется условие
 , , 
|
то ряд (17) в данной области сходится к функции  , т.е. справедливо равенство
, т.е. справедливо равенство
 . .
|
Частный случай ряда Тейлора при  называется рядом Маклорена. Остаток ряда Маклорена в форме Лагранжа имеет вид:
называется рядом Маклорена. Остаток ряда Маклорена в форме Лагранжа имеет вид:
 , ,  , ,
|
а разложение функции в ряд Маклорена, при условии  , выглядит следующим образом:
, выглядит следующим образом:
 . .
|
Если  , то ряд Тейлора (Маклорена), даже если он сходится, имеет сумму, отличную от
, то ряд Тейлора (Маклорена), даже если он сходится, имеет сумму, отличную от  .
.
Ряды Маклорена для некоторых элементарных функций, представленные ниже вместе с их областями сходимости, полезно запомнить для их применения при разложении других, более сложных функций.
 .
.

 .
.

 .
.


 .
.
Последний ряд называется биномиальным, т.к. функция, для которой построен этот ряд, представляет собой бином (двучлен) произвольной степени  . Гарантированная область сходимости биномиального ряда указана для любых значений
. Гарантированная область сходимости биномиального ряда указана для любых значений  ; для некоторых значений она может быть расширена в ту или другую сторону (или в обе) включением в нее границы интервала.
; для некоторых значений она может быть расширена в ту или другую сторону (или в обе) включением в нее границы интервала.
Частные случаи биномиального ряда выглядят следующим образом:
 .
.


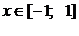 .
.
Из первого частного случая могут быть получены ряды еще для двух часто встречающихся в практических задачах функций:

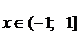 ;
;

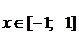 .
.
9. Применение степенных рядов для вычисления функций и определенных интегралов.
Для вычисления значения функции при данном значении аргумента можно воспользоваться разложением этой функции в степенной ряд. В частности, удобно воспользоваться приведенными в предыдущем пункте разложениями в ряд Маклорена функций 

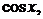


 .
.  Если значение аргумента
Если значение аргумента  принадлежит области сходимости, то после разложения функции в ряд и подстановки
принадлежит области сходимости, то после разложения функции в ряд и подстановки  искомое значение функции представляет собой сумму числового ряда. Поскольку полную сумму ряда, представляющую собой точное значение функции, найти, как правило, затруднительно, то в этом ряде сохраняется такое количество первых членов, которое гарантирует необходимую в данном конкретном случае точность. Точность вычислений задается обычно одной значащей цифрой в каком-либо разряде. Так, запись
искомое значение функции представляет собой сумму числового ряда. Поскольку полную сумму ряда, представляющую собой точное значение функции, найти, как правило, затруднительно, то в этом ряде сохраняется такое количество первых членов, которое гарантирует необходимую в данном конкретном случае точность. Точность вычислений задается обычно одной значащей цифрой в каком-либо разряде. Так, запись 
 означает, что точное значение величины
означает, что точное значение величины  находится в пределах от 5,39 до 5,43. Это можно записать следующим образом:
находится в пределах от 5,39 до 5,43. Это можно записать следующим образом:  . Другими словами, заданная точность
. Другими словами, заданная точность  - это та погрешность, в пределах которой приближенное значение может отличаться от точного.
- это та погрешность, в пределах которой приближенное значение может отличаться от точного.
Для приближенного вычисления определенного интеграла нужно разложить в степенной ряд подынтегральную функцию, проинтегрировать степенной ряд почленно и сохранить в ряде достаточное для обеспечения заданной точности количество его первых членов; при этом область интегрирования не должна выходить за рамки области сходимости ряда.
10. Ряды Фурье.
Функциональный ряд вида

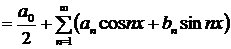 (19)
(19)
называется тригонометрическим рядом.
Если коэффициенты  и
и  вычислены по формулам
вычислены по формулам
 ,
, 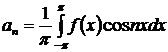 ,
,  , (20)
, (20)
то тригонометрический ряд (19) представляет собой ряд Фурье для функции  , заданной на отрезке
, заданной на отрезке  .
.
Теорема Дирихле. Если  - кусочно гладкая на отрезке
- кусочно гладкая на отрезке  функция, то ее ряд Фурье сходится к функции
функция, то ее ряд Фурье сходится к функции  во всех точках, где она непрерывна. В точках разрыва
во всех точках, где она непрерывна. В точках разрыва 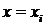 ряд сходится к значению
ряд сходится к значению 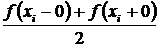 , а на концах интервала – к значению
, а на концах интервала – к значению 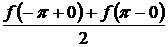 .
.
В силу теоремы Дирихле для функции, заданной на отрезке  и для периодической функции с периодом
и для периодической функции с периодом  в точках непрерывности справедливо равенство:
в точках непрерывности справедливо равенство:
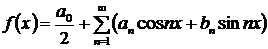 ,
,
где коэффициенты 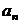 и
и  вычисляются по формулам (20).
вычисляются по формулам (20).
Для четной функции, заданной на отрезке  или для четной с периодом с периодом
или для четной с периодом с периодом  коэффициенты
коэффициенты  при нечетных членах ряда Фурье оказываются нулевыми, и ряд принимает вид
при нечетных членах ряда Фурье оказываются нулевыми, и ряд принимает вид
 ,
,
где
 ;
;  .
.
Аналогично для нечетных функций:
 ;
;  .
.
Ряд Фурье для функции, заданной на отрезке 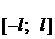 и для периодической функции с периодом
и для периодической функции с периодом  :
:
 ,
,
где
 ,
,  ,
,  .
.
Здесь для четных функций:
 , где
, где  ,
,  ;
;
для нечетных функций:
 , где
, где  .
.
Если требуется представить рядом Фурье функцию, заданную на отрезке  , то ее формально можно доопределить четным или нечетным образом в промежутке
, то ее формально можно доопределить четным или нечетным образом в промежутке  и применить приведенные выше формулы.
и применить приведенные выше формулы.
Решение примерного варианта
Задача 1. Исследовать сходимость числового ряда.
а)  .
.
К данному знакоположительному ряду применим признак Даламбера:
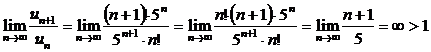 ; ряд расходится.
; ряд расходится.
Ответ: ряд расходится.
б)  .
.
Исследуем данный знакочередующийся ряд на абсолютную сходимость, рассмотрев ряд, составленный из модулей его членов:
 .
.
Полученный знакоположительный ряд сравним по второму признаку сравнения с гармоническим рядом  , про который известно, что он расходится:
, про который известно, что он расходится:
 .
.
Предел существует и не равен нулю; следовательно, согласно признаку, исследуемый ряд, как и гармонический, тоже расходится. Значит, исходный знакочередующийся ряд абсолютной сходимости не имеет.
Проверим теперь, обладает ли исходный знакочередующийся ряд условной сходимостью. Для этого используем признак Лейбница:
 ;
;
 , т.е. для любых
, т.е. для любых  выполняется условие
выполняется условие  .
.
Оба условия признака Лейбница выполняются, т.е. по признаку Лейбница ряд сходится. Таким образом, исходный знакочередующийся ряд сходится условно.
Ответ: ряд сходится условно.
Задача 2. Найти область сходимости степенного ряда.
 .
.
Здесь центр сходимости  . Найдем радиус сходимости по формуле (16), полученной из признака Даламбера:
. Найдем радиус сходимости по формуле (16), полученной из признака Даламбера:
 .
.
Так как при  функции
функции  и
и  являются эквивалентными бесконечно малыми, то при
являются эквивалентными бесконечно малыми, то при  эквивалентны бесконечно малые
эквивалентны бесконечно малые  и
и  , а также
, а также  и
и  . Поэтому
. Поэтому
 .
.
По найденному радиусу сходимости получаем гарантированный интервал абсолютной сходимости:
 .
.
Исследуем сходимость ряда на границах этого интервала.
·  .
.
Этот знакочередующийся ряд не имеет абсолютной сходимости, т.к.
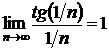 , и ряд
, и ряд  расходится (второй, предельный признак сравнения). В то же время для него выполняются условия
расходится (второй, предельный признак сравнения). В то же время для него выполняются условия  и
и 
 , т.к.
, т.к.  - возрастающая функция. Следовательно, ряд сходится по признаку Лейбница, т.е. исходный степенной ряд в т.
- возрастающая функция. Следовательно, ряд сходится по признаку Лейбница, т.е. исходный степенной ряд в т. 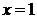 сходится условно.
сходится условно. 
·  .
.
Этот знакоположительный числовой ряд также можно сравнить с расходящимся рядом  по второму признаку сравнения, из чего следует, что ряд
по второму признаку сравнения, из чего следует, что ряд  расходится.
расходится.
Ответ: область сходимости данного степенного ряда:  .
.
Задача 3. Данную функцию представить в виде степенного
ряда по степеням (x – a), где а – данное число.
 .
.
Требуется разложить функцию по степеням двучлена  . Обозначим его новой переменной:
. Обозначим его новой переменной:  . Тогда
. Тогда 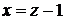 , и
, и  . Последнее выражение представим в виде
. Последнее выражение представим в виде  и введем еще одну переменную:
и введем еще одну переменную:  . После этого
. После этого  . Теперь для функции
. Теперь для функции  применим ее известное разложение в ряд Маклорена (см. справочную информацию):
применим ее известное разложение в ряд Маклорена (см. справочную информацию):
 .
.
В последнем разложении возвратимся к переменной  и далее к исходной переменной
и далее к исходной переменной  :
:

 .
.
Найдем теперь область сходимости. Для переменной 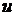 ее составляет интервал
ее составляет интервал 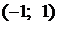 , т.е.
, т.е.  . Тогда
. Тогда  и
и  . Отсюда получаем, что
. Отсюда получаем, что  .
.
Ответ: 
 ,
,  .
.
Задача 4. Вычислить приближенно с заданной точностью 
значение функции при данном значении аргумента
с помощью разложения функции в степенной ряд.
 при
при  .
.
По условию задачи требуется вычислить  с точностью до четвертого знака после запятой. Воспользуемся разложением в ряд Маклорена функции
с точностью до четвертого знака после запятой. Воспользуемся разложением в ряд Маклорена функции 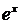 :
:
 .
.
Подставим сюда заданное значение  :
:
 ,
, 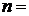 0, 1, 2, …. (а)
0, 1, 2, …. (а)
Здесь в правой части при вычислении нужно учесть такое количество первых членов, чтобы остаток не превышал заданной погрешности:  . При этом ряд в правой части (а) получился знакочередующимся, и для него модуль остатка меньше первого члена этого остатка:
. При этом ряд в правой части (а) получился знакочередующимся, и для него модуль остатка меньше первого члена этого остатка: 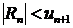 . Следовательно, для обеспечения заданной точности достаточно выполнить условие
. Следовательно, для обеспечения заданной точности достаточно выполнить условие
 . (б)
. (б)
Поскольку
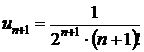 ,
,
то условие (б) принимает вид
 , или
, или  .
.
Методом подбора легко убедиться, что последнее условие начинает выполняться с номера  :
:
 ,
,
 .
.
Следовательно, для обеспечения заданной точности достаточно вычислить сумму первых шести членов ряда, с нулевого по пятый:
 .
.
Ответ:  .
.
Задача 5. Вычислить приближенно с заданной точностью 
определенный интеграл с помощью разложения
подынтегральной функции в степенной ряд.
 .
.
Воспользуемся известным разложением в ряд логарифмической функции:

 .
.
Заменим в этой формуле  на
на  :
:

 .
.
Пересчитаем область сходимости:
 .
.
Констатируем, что интегрирование требуется произвести в пределах области сходимости. Следовательно, ряд, которым представлена подынтегральная функция, можно интегрировать почленно. Выполним это:





 ,
,
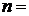 0, 1, 2, …
0, 1, 2, …
Полученный ряд оказался знакочередующимся. Поэтому используем то же самое условие обеспечения заданной точности, что и в предыдущей задаче:
 . (а)
. (а)
Здесь
 ,
,
поэтому минимально необходимое  находим из условия
находим из условия
 , или
, или  :
:

 ,
,

 .
.
Из последнего вытекает, что для обеспечения заданной точности достаточно просуммировать первые шесть членов ряда:

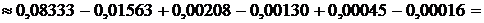
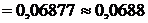 .
.
Ответ:  .
.
Задача 6. Данную функцию  разложить в ряд Фурьев
разложить в ряд Фурьев
заданном интервале.
 , (-1, 1).
, (-1, 1).
Легко убедиться, что в заданном интервале функция непрерывна и, следовательно, может быть представлена своим рядом Фурье в смысле теоремы Дирихле. Кроме того, в рассматриваемом интервале она четная, поэтому ее ряд Фурье должен содержать только четные тригонометрические функции, т.е. косинусы. На этих основаниях записываем:
 ,
,  . (а)
. (а)
Находим коэффициенты.
 .
.
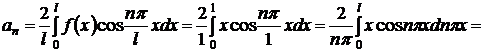

 .
.
Т.к. 
 , то
, то  . Тогда
. Тогда
 .
.
Далее, 
 ,
,