Лекция 16
Дифференциальные уравнения второго порядка
Вопросы:
1. Дифференциальныеуравнения второго порядка.
2. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Их решение.
3. Решение линейных однородных уравнений с постоянными коэффициентами.
4. Метод подбора частного решения линейного неоднородного уравнения второго порядка.
Дифференциальные уравнения второго порядка
Определение 9.17. Дифференциальным уравнением второго порядка называется дифференциальное уравнение, которое имеет вид

 (9.6)
(9.6)
Определение 9.18. Общим решением дифференциального уравнения второго порядка называется функция  которая зависит от произвольных постоянных С 1 и С 2 и при этом выполнены условия:
которая зависит от произвольных постоянных С 1 и С 2 и при этом выполнены условия:
1) она удовлетворяет дифференциальному уравнению (9.6) при любых конкретных значениях С 1 и С 2;
2) каковы бы ни были начальные условия 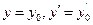 при
при  , существуют
, существуют 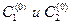 , такие, что функции
, такие, что функции  и
и  удовлетворяют начальным условиям.
удовлетворяют начальным условиям.
Функция  — частное решение (9.6).
— частное решение (9.6).
Рассмотрим наиболее простой вид дифференциальных уравнений второго порядка — линейные дифференциальные уравнения с постоянными коэффициентами.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение 9.19. Дифференциальное уравнение второго порядка называется линейным, если оно содержит только первые степени  , т.е. имеет вид
, т.е. имеет вид
 , (9.7)
, (9.7)
где  могут быть некоторыми функциями от х, причем
могут быть некоторыми функциями от х, причем  . Мы рассмотрим только случай, когда
. Мы рассмотрим только случай, когда  — некоторые константы. Если
— некоторые константы. Если  уравнение называется неоднородным. Если
уравнение называется неоднородным. Если 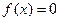 , т.е. уравнение вида
, т.е. уравнение вида
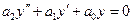 (9.8)
(9.8)
называется однородным.
Теорема 1. Если  и
и 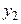 — решения уравнения
— решения уравнения 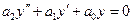 , такие, что их отношение не равно постоянной величине
, такие, что их отношение не равно постоянной величине 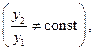 то линейная комбинация этих функций
то линейная комбинация этих функций  является общим решением уравнения.
является общим решением уравнения.
Теорема 2. Общее решение неоднородного уравнения  можно составить как сумму общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения.
можно составить как сумму общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения.

Таким образом, чтобы найти решение неоднородного линейного уравнения, необходимо уметь решать однородные уравнения.
Решение линейных однородных уравнений с постоянными коэффициентами
Вспомним линейное однородное уравнение первого порядка (пример 9.4)  , его общее решение
, его общее решение  . Проверим, можно ли найти частное решение однородного линейного дифференциального уравнения второго порядка (9.8) в виде
. Проверим, можно ли найти частное решение однородного линейного дифференциального уравнения второго порядка (9.8) в виде 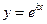 , k=const.
, k=const.
Тогда 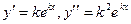 и подставив в (9.8), находим
и подставив в (9.8), находим
 .
.
Так как  , то
, то
 . (9.9)
. (9.9)
Следовательно,  является решением уравнения (9.8) в том случае, когда k удовлетворяет (является корнем) уравнению (9.9), которое называется характеристическим уравнением.
является решением уравнения (9.8) в том случае, когда k удовлетворяет (является корнем) уравнению (9.9), которое называется характеристическим уравнением.
Как известно, корни квадратного уравнения зависят от знака дискриминанта, поэтому рассмотрим соответствующие три случая.
I.  . Корни характеристического уравнения различны
. Корни характеристического уравнения различны  . В этом случае частные решения
. В этом случае частные решения  , условие
, условие  выполнено. Следовательно, общее решение однородного уравнения имеет вид:
выполнено. Следовательно, общее решение однородного уравнения имеет вид:
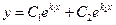 .
.
Пример 9.8. Решить уравнение 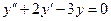 .
.
Решение. Характеристическое уравнение имеет вид:
 ,
, 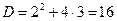 ,
,  .
.
 .
.
Общее решение  .
.
II.  Корни характеристического уравнения равны
Корни характеристического уравнения равны  .
.
Как и ранее  . Можно проверить, что
. Можно проверить, что  является решением уравнения (9.8) и
является решением уравнения (9.8) и  .
.
Значит, общее решение однородного уравнения в этом случае имеет вид
 .
.
Пример 9.9. Решить уравнение  .
.
Решение. Вид характеристического уравнения
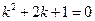 ,
, 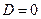 ,
, 
 .
.
Общее решение  .
.
III. 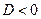 . Действительных решений характеристическое уравнение не имеет, но имеет комплексные корни
. Действительных решений характеристическое уравнение не имеет, но имеет комплексные корни  . Определяем числа
. Определяем числа  , тогда
, тогда  и
и  — частные решения уравнения (9.8) и
— частные решения уравнения (9.8) и  .
.
Общее решение уравнения имеет вид
 .
.
Пример 9.10. Найти частное решение уравнения 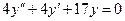 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 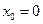 ,
,  ,
,  .
.
Решение. Вид характеристического уравнения
 ,
,
 ,
,  .
.
 и общее решение
и общее решение  .
.
Чтобы определить  и
и  , найдем y'.
, найдем y'.
 и, подставив начальные условия в у и y', получим
и, подставив начальные условия в у и y', получим




Частное решение, удовлетворяющее начальным условиям
 .
.