Метод подбора частного решения линейного неоднородного уравнения второго порядка

При применении этого метода рассматриваются только определенного вида функции f (x), стоящие в правой части уравнения (9.7). При этом надо учитывать, что значения корней характеристического уравнения могут изменить вид частного решения.

1.1. Пусть правая часть имеет вид , k ₀≠ k ₁, k ₀≠ k ₂, где k ₁ и k ₂ – корни характеристического уравнения, тогда .

1.2. ,в характеристическом уравнении (9.9) k ₀= k ₁, k ₀≠ k ₂ (или k ₀≠ k ₁, k ₀= k ₂). Тогда .

1.3. , k ₀= k ₁= k ₂, тогда .

2.1. , т.е. правая часть некоторый многочлен от х, . В частности, , , .

В этом случае, если в характеристическом уравнении (9.9) k ₁≠0, k ₂≠0, то частное решение — многочлен той же степени с неопределенными коэффициентами.

2.2. 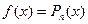, k ₁=0, k ₂≠0, тогда .

2.3. 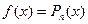, k ₁= k ₂=0, тогда .

3.1. . Если в характеристическом уравнении (9.9) ≠0, а 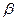— любое или =0, а , то .

3.2. . Тогда если в характеристическом уравнении =0 и , то .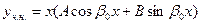

3.3. и числа не являются решениями соответствующего характеристического уравнения (9.9), то частное решение можно искать в виде , где — многочлены степени с неопределенными коэффициентами.

3.4. и числа являются решениями соответствующего характеристического уравнения (9.9), то частное решение можно искать в виде .

Пример 9.11. Найти частное решение дифференциального уравнения с начальными условиями .

Решение. Решение исходного уравнения разобьем на этапы.

1. Составим и решим характеристическое уравнение .

Общее решение уравнения соответствующего однородного уравнения:

.

2. Подбором находим вид частного решения. Так как 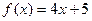, то , то это соответствует случаю 2.2 и

Подставив в исходное уравнение, получаем

Выписываем коэффициенты при одинаковых функциях:

Решая полученную систему, находим: A=-1, B=-3,5 и, следовательно, .

3. Общее решение неоднородного уравнения:

.

4. Для вычисления значений С₁ и С₂ надо найти : . Подставляя начальные условия в y и , получим систему уравнений

Отсюда С₂=3, С₁=-2.

Итак, частное решение, удовлетворяющее начальным условиям, имеет вид:

.

Пример 9.12. Найти общее решение уравнения .

Решение. Составим и решим характеристическое уравнение

.

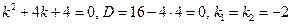Общее решение однородного уравнения 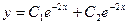. Тогда частное решение неоднородного уравнения будем искать в виде , т.к. . Найдем производные и подставим в исходное уравнение:

, ,

,

.

Приравниваем коэффициенты при одинаковых функциях в правой и левой части уравнения:

, тогда .

Составим общее решение неоднородного уравнения

.

Пример 9.13. Найти частное решение .

Решение. 1. Характеристическое уравнение:

.

Общее решение однородного уравнения:

2. , т.е. . Следовательно, вид частного решения:

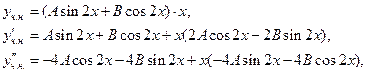
Подставляем найденные производные в уравнение:

.

.

Приравниваем коэффициенты при функциях:

и .

3. Общее решение неоднородного уравнения:

.

4. Найдем числовые значения С₁ и С₂:

.

Отсюда

Частное решение, удовлетворяющее начальным условиям, имеет вид:

.

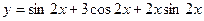Пример 9.14. Продолжим изучение зависимости между ценой p, спросом d и предложением s.

Согласно модели Вальраса, регулирование цены в условиях конкуренции можно описать с помощью дифференциального уравнения:

p' = α (d-s),

где α >0 — некоторый постоянный множитель. Как изменится цена в условиях нереализованного (хранимого) товара?

Решение. Предположим, что существует тенденция уменьшения цены не только в условиях избыточного предложения, но и при наличии непроданного товара, то есть:

p'=α (d-s) -β .

Последнее выражение суммирует разности между величиной спроса и предложения за предшествующий период.

Тогда в дифференциальной форме:

p''=α (d′-s′)- β (s-d).

Если (см. раздел 1) s=a₀+a₁p, d=b₀+b₁p, то получим следующее линейное дифференциальное уравнение второго порядка:

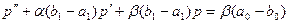(9.10)

В том случае, когда корни характеристического уравнения k ₁ и k ₂ действительны и k ₁≠ k ₂, то имеем следующее общее решение однородного уравнения:

.

Предположим, что в начальный момент времени р′=0, р′′=0, тогда частное решение неоднородного уравнения имеет вид:

.

Следовательно, общее решение уравнения (9.10):

.

 

 

ЛИТЕРАТУРА

 

Для содержательных модулей

1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.

2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.

 

Основная

1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.

2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.

3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.

4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.

5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.

6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.

7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.

8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.

 

Сборники задач

1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.

2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.