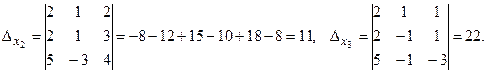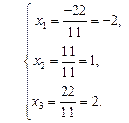Лекция 2 СИСТЕМЫЛИНЕЙНЫХ УРАВНЕНИЙ
Вопросы:
1. Решение систем линейных уравнений.
2. Правило Крамера.
3. Условия совместности и определенности систем линейных уравнений.
4. Теорема Кронекера-Капелли.
5. Решение систем n-линейных уравнений с m неизвестными.
6. Решение систем линейных уравнений методом Гаусса.
7. Однородные системы линейных уравнений.
Основные определения. Матричная форма записи систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными
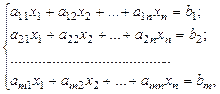(1.6)
где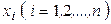 
— неизвестные переменные величины, 
— произвольные числа, называемые коэффициентами при неизвестных, 
— некоторые числа, называемые свободными членами уравнений.
Определение 1.15. Решением этой системы называется совокупность n чисел 
которые, будучи подставлены вместо неизвестных в уравнения, обращают эти уравнения в тождества.
Определение 1.16. Система уравнений называется совместной, если она имеет хотя бы одно решение. Если же система не имеет ни одного решения, то она называется несовместной.
Определение 1.17. Две системы называются равносильными, или эквивалентными, если они имеют одно и то же множество решений. Все несовместные системы эквивалентны между собой.
Определение 1.18. Совместная система называется определенной, если она имеет только одно решение, и неопределенной, если она имеет более одного решения.
При решении систем используют три основных действия, как и ранее называемые элементарными преобразованиями, которые не меняют эквивалентность систем.
1. Строки можно менять местами.
2. Строки можно делить и умножать на число, не равное нулю.
3. Строки можно складывать (к одной строке можно прибавить другую строку, умноженную на любое число).
|
|
4. Можно отбрасывать стоку, у которой все аij =0 и bj =0, 
.
Cистемы уравнений удобно записывать в матричной форме. Обозначим
где А — матрица системы, В — матрица-столбец свободных членов, Х — матрица-столбец неизвестных.
Произведение 
есть матрица–столбец, элементами которой являются левые части системы (1.6). На основании определения равенства матриц систему (2.6) можно записать в виде
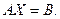(1.7)
Метод обратной матрицы решения систем n-линейных уравнений с n неизвестными
Рассмотрим систему 
Если ввести матрицы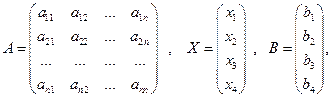 
то эту систему, как говорилось выше, можно записать в виде (1.7). Если матрица А невырождена, то умножив слева на А -1, получим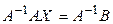 
, 
, то есть
. (1.8)
С помощью метода обратной матрицы можно решать квадратные системы, в которых количество уравнений равно количеству неизвестных и определитель системы отличен от нуля.
Пример 1.18. Решить матричным способом систему: 
.
Решение. Обозначим через А — матрицу из коэффициентов при неизвестных, через X — столбец из неизвестных. В — столбец из свободных членов, то есть:
.
Тогда данную систему можно записать в виде одного матричного уравнения: 
.
Произведение 
существует, так как число столбцов матрицы А равно числу строк матрицы Х. Находим матрицу А -1:
;
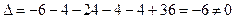Поскольку матрица А невырожденная, решением системы будет:
или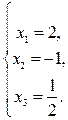 
Метод Крамера решения систем линейных уравнений
Рассмотрим систему n линейных уравнений с n неизвестными (число неизвестных равно числу уравнений), то есть квадратную систему
(1.9.)
Обозначим определитель матрицы системы через D: 
, (1.10)
|
|
∆ называют основным или главным определителем системы (1.9), а через 
— определители, образованные заменой в определителе системы соответствующих столбцов столбцом свободных членов:
. (1.11)
Теорема Крамера. Если определитель D системы (1.9) не равен нулю, то решение этой системы находится по формулам:
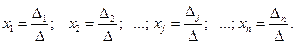(1.12)
Если D = 0, то правило Крамера применять нельзя и систему решают другим методом или устанавливают ее несовместность. Формулы Крамера являются следствием метода обратной матрицы.
Пример 1.19. Решить систему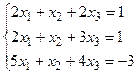 
по правилу Крамера.
Решение.
