Теорема Кронекера-Капелли дает правило для определения разрешимости системы без указания способа нахождения решения. Рассмотрим вопрос о разрешимости систем линейных уравнений.
Пусть задана система m линейных уравнении с n неизвестными (1.6).
Определение 1.19. Матрица  (1.13)
(1.13)
называется расширенной матрицей системы (1.6).
Теорема Кронекера-Капелли. Для совместности системы (1.6) необходимо и достаточно, чтобы ранг матрицы системы (1.6) равнялся рангу расширенной матрицы этой системы.
Итак, система (2.6) совместна тогда и только тогда, если  В этом случае число r называется рангом системы.
В этом случае число r называется рангом системы.
Пример 1.20. Исследовать систему уравнений 
Решение. Определим ранги матрицы системы и расширенной матрицы системы. Выпишем расширенную матрицу системы  .
.
Вертикальной чертой мы отделили элементы матрицы системы (матрицы А) от свободных членов системы. Проведем следующие элементарные преобразования: прибавим к элементам второй строке соответствующие элементы третьей строки:
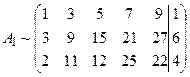 .
.
Разделим все элементы второй сроки на 3:  .
.
Вычтем из элементов второй строки соответствующие элементы первой строки:

Отсюда видно, что 
Нетрудно видеть, что  Следовательно, система несовместна.
Следовательно, система несовместна.
Метод Гаусса
Метод Гаусса — метод последовательного исключения неизвестных — заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последних (по номеру) неизвестных находят все остальные неизвестные.
Рассмотрим решение системы (1.6). Предположим, что  (если это не так, то перестановкой уравнений местами добьемся того, что на месте
(если это не так, то перестановкой уравнений местами добьемся того, что на месте 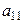 будет коэффициент не равный нулю).
будет коэффициент не равный нулю).
Шаг 1. Умножая первое уравнение на подходящие числа (а именно на 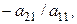
 …,
…, 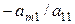 ) и прибавляя полученные уравнения соответственно ко второму, третьему, …, m -му уравнению системы, исключим неизвестную
) и прибавляя полученные уравнения соответственно ко второму, третьему, …, m -му уравнению системы, исключим неизвестную 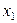 из всех последующих уравнений, начиная со второго. Получим
из всех последующих уравнений, начиная со второго. Получим

Буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.
Шаг 2. Предположим, что 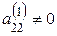 (если это не так, то соответствующей перестановкой уравнений или неизвестных с изменением их номеров добьемся того, чтобы
(если это не так, то соответствующей перестановкой уравнений или неизвестных с изменением их номеров добьемся того, чтобы 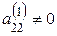 ). Умножая второе уравнение на подходящие числа (
). Умножая второе уравнение на подходящие числа (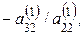
 …,
…,  ) и прибавляя полученные уравнения соответственно к третьему, четвертому,…, m -му уравнению системы, исключим неизвестную
) и прибавляя полученные уравнения соответственно к третьему, четвертому,…, m -му уравнению системы, исключим неизвестную  из всех последующих уравнений, начиная с третьего.
из всех последующих уравнений, начиная с третьего.
Продолжая процесс последовательного исключения неизвестных  после
после  -го шага получим систему
-го шага получим систему
 (1.14)
(1.14)
Число нуль в последних уравнениях означает, что их левые части имеют вид  . Если бы хотя одно из чисел
. Если бы хотя одно из чисел  не равно нулю, то соответствующее равенство противоречиво, и система несовместна. Таким образом, для любой совместной системы числа
не равно нулю, то соответствующее равенство противоречиво, и система несовместна. Таким образом, для любой совместной системы числа 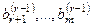 равны нулю и в этом случае последние
равны нулю и в этом случае последние  уравнений являются тождествами и их отбрасывают. После отбрасывания лишних уравнений возможно два случая:
уравнений являются тождествами и их отбрасывают. После отбрасывания лишних уравнений возможно два случая:
1) число оставшихся уравнений равно числу переменных, т.е.  . В этом случае система имеет треугольный вид и единственное решение;
. В этом случае система имеет треугольный вид и единственное решение;
2)  . В этом случае система имеет бесконечно много решений.
. В этом случае система имеет бесконечно много решений.
Переход системы к эквивалентной последней системе называется прямым ходом метода Гаусса, а нахождение значения неизвестных, начиная с последнего, — обратным ходом.
Надо отметить, что при конкретном решении систем, часто изменяют последовательность действий.
Пример 1.22. Решить систему методом Гаусса. Проверить совместность системы. Найти одно общее и одно базисное решение.
Решение. Систему решаем методом Гаусса:
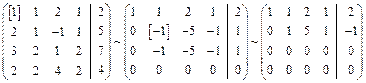 ,
,
 ,
,
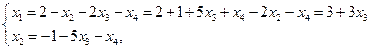
х 3, x 4 — свободные неизвестные, x 1, x 2 — базисные неизвестные. Положив 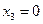 и
и 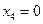 , получим базисное решение:
, получим базисное решение:  .
.

Пример 1.23. Решить систему 
Решение.


Так как ранги матриц не совпадают, то система несовместная.
ЛИТЕРАТУРА