Сборник заданий
Для расчетно-графических работ
По математике
Для студентов заочного отделения всех направлений
Уфа 2017
Рекомендовано к изданию методической комиссией механического факультета (протокол № 1 от 29 августа 2017 года)и заседанием кафедры математики (протокол № 10 от 28 июня 2017 года)
Составители:
доцент Ардуванова Ф.Ф., ст. преподаватель Зиянгирова С.Р.
Рецензент:
доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск:
и.о. зав. кафедрой математики, доцент Бадретдинов И.Д.
Оглавление
| Введение | |
| Решение типовых задач Задание 1 | |
| Задание 2 | |
| Задание 3 | |
| Задание 4 | |
| Задание 5 | |
| Задание 6 | |
| Задание 7 | |
| Задание 8 | |
| Задание 9 | |
| Задание 10 | |
| Задание 11 | |
| Задание 12 | |
| Задание 13 | |
| Задание 14 | |
| Задание 15 | |
| Задание 16 | |
| Задание 17 | |
| Задание 18 | |
| Задание 19 | |
| Задание 20 | |
| Задание 21 | |
| Задание 22 | |
| Варианты индивидуальных заданий | |
| Библиографический список | |
Введение
Сборник заданий для выполнения расчетно-графических работ по математике предназначен для студентов заочного отделения всех направлений. Сборник включает в себя, помимо заданий, краткие указания к выполнению контрольных и расчетно-графических работ, образцы решения некоторых задач, контрольные задания.
Перед выполнением контрольной работы студенту необходимо изучить соответствующие разделы рекомендуемой литературы [1] – [3] и воспользоваться решениями типовых примеров, содержащихся в настоящем сборнике. Большое количество образцов решенных задач дано в руководстве к решению задач [5] и [7]. Задачи для самостоятельного решения имеются как в представленных методических указаниях, так и в сборниках задач [4 ‑ 6].
Номер варианта по каждому заданию студент выбирает на усмотрение преподавателя: по номеру в списке студентов группы или по формуле  ,
,
где 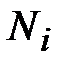 - номер варианта,
- номер варианта,
 - номер задания,
- номер задания,
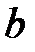 - предпоследняя цифра шифра студента,
- предпоследняя цифра шифра студента,
 - последняя цифра шифра.
- последняя цифра шифра.
Пример.
Пусть шифр студента 1235, тогда:
номер варианта первого задания:  =
=  ;
;
номер варианта второго задания: 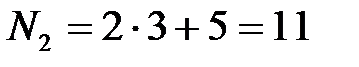 ;
;
номер варианта третьего задания:  ;
;
номер варианта четвертого задания:  .
.
Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
Если итоговая цифра по формуле получится число больше 30, то для определения варианта от полученной цифры вычитают 30.
Пример.
Пусть шифр студента 1298.
Номер варианта третьего задания:  . Промежуток 36 ‑ 30=6. Таким образом, в третьем задании студент решает задачу вариант №6.
. Промежуток 36 ‑ 30=6. Таким образом, в третьем задании студент решает задачу вариант №6.
Решение типовых задач
Задание 1
Решить систему линейных уравнений
а) методом Крамера; б) методом Гаусса:

Решение:
а) Решим систему методом Крамера. Составим матрицу системы:

Вычислим определитель этой матрицы:

Находим определители  получающиеся из исходного определителя заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
получающиеся из исходного определителя заменой соответственно первого, второго и третьего столбцов столбцом свободных членов: 




Теперь используя формулы Крамера  находим решение системы:
находим решение системы:

б) Решим систему уравнений методом Гаусса.
Этот метод заключается в последовательном исключении переменных из системы уравнений.
Составим расширенную матрицу системы, в которую входят коэффициенты при переменных и свободные члены:

Чтобы исключить переменную  из второго и третьего уравнений, умножим первую строку на (-2) и (-3) и полученные строки прибавим ко второй и третьей строке соответственно:
из второго и третьего уравнений, умножим первую строку на (-2) и (-3) и полученные строки прибавим ко второй и третьей строке соответственно:

Чтобы исключить переменную  из третьего уравнения, умножим вторую строку на (-1) и полученные строку прибавим к строке:
из третьего уравнения, умножим вторую строку на (-1) и полученные строку прибавим к строке:

Получили систему уравнений, равносильную исходной системе, в которой первое уравнение содержит три переменных, второе - две, а третье - одну переменную:

Отсюда последовательно находим: 
Проверяем полученное решение, подставляя найденные значения в исходную систему:

Получили тождественные равенства, следовательно, система решена правильно.
Задание 2
Даны координаты вершин треугольника АВС A(-1; 2), B(5;-1), C(-4;-5).
Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и ВС, их угловые коэффициенты;
3) найти величину угла В;
4) уравнение медианы АЕ;
5) уравнение и длину высоты СД;
6) уравнение прямой, проведенной через точку Е, параллельно стороне АВ;
7) сделать чертеж.
Решение.
1) Расстояние d между точками  и
и  определяется по формуле
определяется по формуле


воспользовавшись, которой находим длину AB:

2) Уравнение прямой, проходящей через две заданные точки плоскости 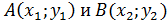 , имеет вид
, имеет вид

Подставляя в это уравнение координаты точек А и В, получим уравнение стороны АВ:




 (AB)
(AB)
Угловой коэффициент  прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом
прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом 
Имеем  откуда
откуда  , откуда
, откуда  .
.
Аналогично получим уравнение прямой BC и найдем ее угловой коэффициент:
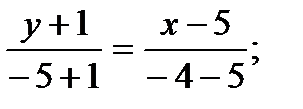



Далее


 , т.е.
, т.е.  .
.
3) Для нахождения внутреннего угла нашего треугольника воспользуемся формулой

Подставив ранее вычисленные значения  в эту формулу, находим:
в эту формулу, находим:

| M |
| y |
| x |
| F |
| D |
| E |
| C |
| B |
| A |
Теперь воспользовавшись инженерным микрокалькулятором, получаем
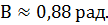
4) Для составления уравнения медианы АЕ найдем сначала координаты точки Е ‑ середины отрезка BC;


Теперь подставив в  координаты точек A и B, получим уравнение медианы:
координаты точек A и B, получим уравнение медианы:




 (AE)
(AE)
5) Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку  с заданным угловым коэффициентом k, которое имеет вид
с заданным угловым коэффициентом k, которое имеет вид
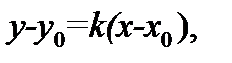
и условием перпендикулярности прямых AB и CD, которое выражается соотношением  откуда
откуда  Подставив в
Подставив в  вместо k – значение
вместо k – значение  , а вместо
, а вместо  ‑ координаты точки С, получим уравнение высоты CD:
‑ координаты точки С, получим уравнение высоты CD:


 (CD)
(CD)
Для вычисления длины высоты CD воспользуемся формулой отыскания расстояния d от заданной точки  до заданной прямой с уравнением
до заданной прямой с уравнением  ,которая имеет вид
,которая имеет вид

Подставив в эту формулу вместо  ‑ координаты точки C, а вместо A, B, C ‑ коэффициенты уравнения прямой AB, получаем
‑ координаты точки C, а вместо A, B, C ‑ коэффициенты уравнения прямой AB, получаем

6) Так как искомая прямая EF параллельна прямой AB, то
 . Подставив в уравнение
. Подставив в уравнение  , вместо
, вместо 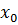 , координаты точки E, а вместо k значение
, координаты точки E, а вместо k значение  , получаем уравнение прямой EF:
, получаем уравнение прямой EF:
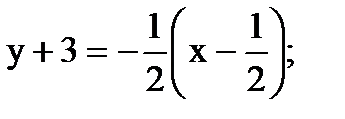


 (EF)
(EF)
Для отыскания координат точки M решаем совместно уравнения прямых EF и CD:

Таким образом, 
7) Треугольник ABC, высота CD, медиана AE, прямая EF и точка M построены в системе координат xOу на рис. 1.
Задание 3
Даны координаты вершин пирамиды ABCD: A (0; 0; 1), B (2; 3; 5), C (6; 2; 3), D (3; 7; 2).
Требуется:
1) Записать векторы  в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) Найти угол между векторами  ;
;
3) Найти проекцию вектора  на вектор
на вектор  ;
;
4) Найти площадь грани  ;
;
5) Найти объем пирамиды  ;
;
6) Составить уравнение ребра  ;
;
7) Составить уравнение грани  .
.
Решение: 1) Известно, что произвольный вектор a представляется в системе орт  по формуле
по формуле

 (1)
(1)
где 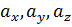 - координаты вектора
- координаты вектора  в системе координат, порожденной ортами, причем
в системе координат, порожденной ортами, причем
 ,
,  .
.
Если заданы точки  то для вектора
то для вектора 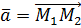 координаты будут следующими
координаты будут следующими 
 ,
,  , то есть
, то есть
 (2)
(2)
Воспользовавшись формулой (2) и координатами заданных точек A, B, C, D, получим:
| А |
| В |
| С |
| D |



Если вектор  задан формулой (1), то его модуль вычисляется следующим образом:
задан формулой (1), то его модуль вычисляется следующим образом:
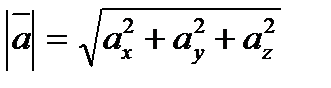 (3)
(3)
Используя формулу (3), получаем модули найденных векторов
 ,
,  ,
,  .
.
2) Известна формула

где  ‑ скалярное произведение векторов и, которое можно вычислить следующим образом:
‑ скалярное произведение векторов и, которое можно вычислить следующим образом:

Имеем

то есть 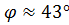
3) Известно, что

то есть в нашем случае

4) Воспользуемся формулой нахождения площади треугольника, построенного на векторах 
 ,
, 

где  – векторное произведение векторов, которое можно вычислить по следующему правилу:
– векторное произведение векторов, которое можно вычислить по следующему правилу:

В нашем примере  причем
причем

Таким образом,
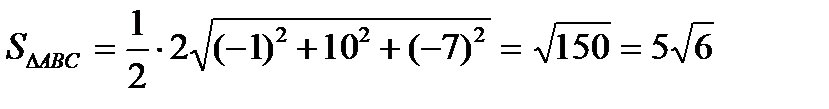 (кв.ед).
(кв.ед).
5) Объем пирамиды, построенной на трех некомпланарных векторах  можно найти по формуле
можно найти по формуле

где  - смешанное произведение векторов, которое вычисляется следующим образом:
- смешанное произведение векторов, которое вычисляется следующим образом:

У нас 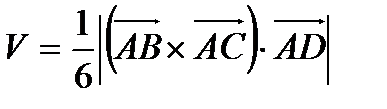 , где
, где 

то есть  .
.
6) Известно, что уравнение прямой, проходящей через две заданные точки пространства  и имеет вид:
и имеет вид:
 (4)
(4)
Подставив в (4) Координаты точек A и C получим
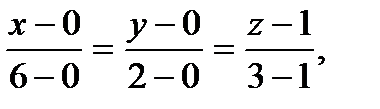
то есть уравнение ребра AC окончательно запишется следующим образом:
 или
или 
7) Уравнение плоскости, проходящей через три заданные точки  можно записать в виде
можно записать в виде

Подставляя в него координаты точек A, B, C, получим



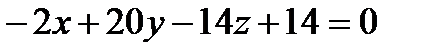 ;
; 
Задание 4
Вычислить пределы:
 ;
;
г)  ; д)
; д) 
Решение:
а) 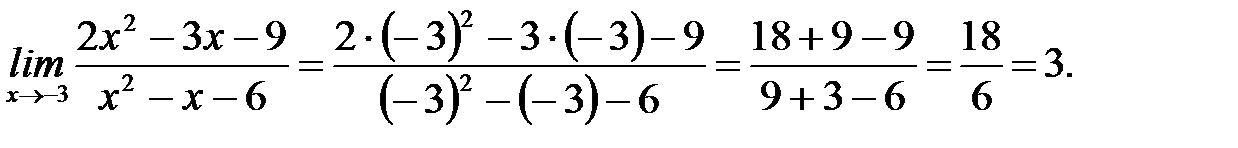
б)  Подставив предельное значение аргумента в заданное выражение, получим неопределенность вида
Подставив предельное значение аргумента в заданное выражение, получим неопределенность вида  , для раскрытия которой числитель и знаменатель дроби разложим на множители, найдя предварительно корни трехчленов.
, для раскрытия которой числитель и знаменатель дроби разложим на множители, найдя предварительно корни трехчленов.

в)  Подстановка предельного значения х показывает, что имеем неопределенность вида
Подстановка предельного значения х показывает, что имеем неопределенность вида  , для раскрытия которой числитель и знаменатель дроби делим почленно на
, для раскрытия которой числитель и знаменатель дроби делим почленно на  . При этом получим пределы вида
. При этом получим пределы вида 
 и т. д., которые равны нулю.
и т. д., которые равны нулю.
 .
.
г) Преобразуем данное выражение: 
В каждом сомножителе выполним несложные преобразования, позволяющие применить первый замечательный предел:
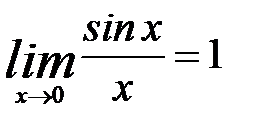 , или
, или  . Тогда
. Тогда
 .
.
д) Преобразуем исходное выражение так, чтобы использовать второй замечательный предел:  или
или  .Выделим внутри скобки единицу, сделаем замену переменной и преобразуем показатель степени.
.Выделим внутри скобки единицу, сделаем замену переменной и преобразуем показатель степени.

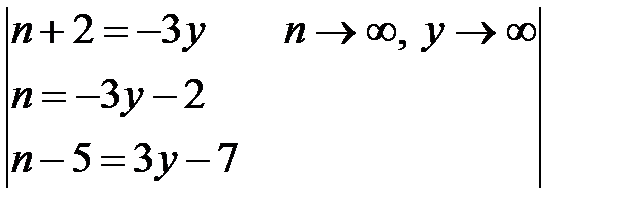 =
=
= 
 =
=  .
.
Задание 5
Найти производные функций:

Решение. При вычислении производных используют правила дифференцирования и таблицу производных.
Правила дифференцирования:
1. (с)  =0 2. (u+v)
=0 2. (u+v)  =u
=u  +v
+v  3. (uv)
3. (uv)  =u
=u  v+uv
v+uv 
4. (сu)  = сu
= сu  5.
5. 
 .
.
Таблица производных основных элементарных функций:
1.  , в частности:
, в частности:  ;
;
2.  , в частности:
, в частности:  ;
;
3.  , в частности:
, в частности:  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8. 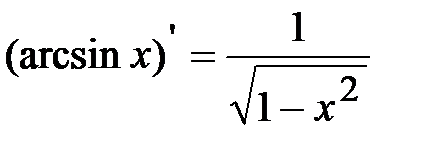 ;
;
9.  ;
;
10.  ;
;
11.  .
.
а) Используя правило дифференцирования суммы функций и таблицу производных, получим:
 .
.
б) Воспользуемся правилом дифференцирования произведения двух функций и формулами нахождения производной от показательной и логарифмической функции.
 =
=  .
.
в) Найти производную функции:  .
.
Используем правило дифференцирования дроби и формулы нахождения производной от  и показательной функции.
и показательной функции.
 .
.
Задание 6
Исследовать функцию методами дифференциального исчисления и построить ее график: a)  .
.
Решение. При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:
1. Найти область определения функции.
2. Найти точки пересечения графика с осями координат, если это возможно.
3. Найти асимптоты графика функции.
4. Найти интервалы монотонности и точки экстремума функции.
5. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
На основании полученного исследования построить график.
1. Область определения.
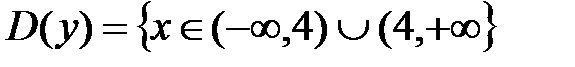 .
.
2. Асимптоты графика:
а) вертикальная 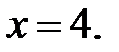
б) наклонная  , где
, где
 .
.

3. Найдем производную функции.
 ;
;  ;
;  .
.
 .
.
Определим знак производной в промежутках:
| xx | ( ) )
| (2, 4) | (4, 10) | (10, +  ) )
| |||
x 
| + | - | не сущ. | - | + | ||
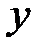 y y
| max | min |

4. Найдем вторую производную функции.

 x x
| ( ) )
| (4, +  ) )
| |
 
| - | не сущ. | + |
 y y
| 
| 
|
Точек перегиба графика функции нет.
По результатам исследования построим график функции.
| y |
| -4 |
| x |
Задание 7.
Найти неопределенный интеграл методом подстановки 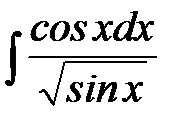 .
.
Решение. При нахождении неопределенных интегралов используется таблица интегралов:
| 1) |  , ,  , ,
| 7) | 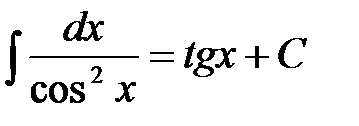
|
| 2) | 
| 8) | 
|
| 3) | 
| 9) | 
|
| 4) | 
| 10) | 
|
| 5) | 
| 11) | 
|
| 6) | 
| 12) | 
|
В нашем случае имеем
 .
.
Задание 8
Найти неопределенные интегралы, используя выделение полного квадрата  .
.
Решение:


Задание 9
Найти неопределенные интегралы, применяя метод интегрирования по частям: а)  ; б)
; б) 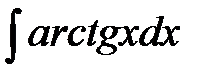 .
.
Решение. а) Используем формулу для интегрирования по частям  .
.
Пусть  . Тогда
. Тогда  Следовательно,
Следовательно, 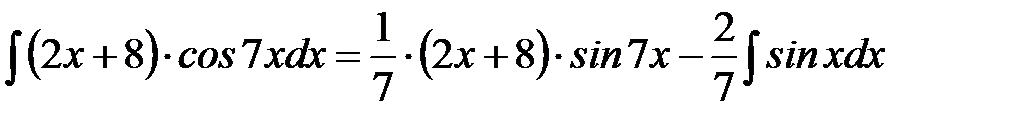 =
=
=  .
.
б) 
 .
.
Задание 10
Найти неопределенный интеграл, пользуясь разложением рациональных дробей на простейшие  .
.
Решение.
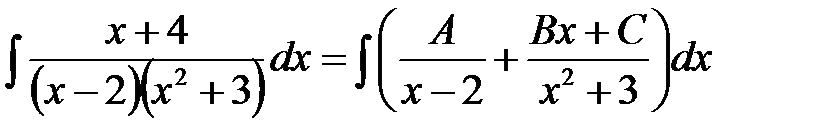 .
.
После приведения к общему знаменателю получим следующее тождество для числителей:
 или
или  .
.
Этим тождеством мы и воспользуемся для нахождения коэффициентов
А, В и С, приравняв коэффициенты при одинаковых степенях левой и правой частей тождества:
 .
.
В результате получим:
 , для второго интеграла введем подстановку
, для второго интеграла введем подстановку  .
.
Окончательно, получим
 .
.
Задание 11
Вычислить площадь, ограниченную заданными параболами.
 .
.
Решение: Найдем точки пересечения кривых  ,
, 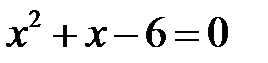 ,
,  . Используя формулу для вычисления площади плоской фигуры, ограниченной кривыми
. Используя формулу для вычисления площади плоской фигуры, ограниченной кривыми  ,
,  и прямыми
и прямыми  :
:
| у = х2 ‑ 4х |
| у = 2х2 ‑ 3х ‑ 6 |
| у |
| х |
| ‑3 |
| 2 |


Задание 12
Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью Ох,  .
.
Решение: Найдем точки пересечения кривых  ,
, 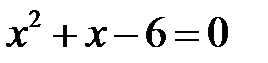 ,
,  .
.
| у = х2 |
| у |
| х |
| 6 |
| 2 |
| 6 |
| В |
| А |
| К |
| О |
 ,
,  ,
, 
 ;
; 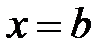 вокруг оси
вокруг оси  , получим тело вращения, объем которого находим по формуле:
, получим тело вращения, объем которого находим по формуле:
 .
.
 Разобьем фигуру на две части: ОАК и АКВ. Применительно к нашему случаю, имеем объем всей фигуры
Разобьем фигуру на две части: ОАК и АКВ. Применительно к нашему случаю, имеем объем всей фигуры

Задание 13
Найти частное решение уравнения  , удовлетворяющее условию
, удовлетворяющее условию  .
.
Решение: Запишем, что  , тогда нное уравнение является уравнением с разделяющимися переменными. Умножив обе части уравнения на dx и разделив на множитель (y+ 1), получим уравнение с разделёнными переменными.
, тогда нное уравнение является уравнением с разделяющимися переменными. Умножив обе части уравнения на dx и разделив на множитель (y+ 1), получим уравнение с разделёнными переменными.
 или
или 

Интегрируя, имеет: 
In  =In sin x +In C, y+1=С sin x, y=C sin x—1—общее решение заданного уравнения. Используя начальные условия, находим значения постоянной производной C.
=In sin x +In C, y+1=С sin x, y=C sin x—1—общее решение заданного уравнения. Используя начальные условия, находим значения постоянной производной C.
2=Сsin  —1; 2= C—1; C=3.
—1; 2= C—1; C=3.
Следовательно, y=3sin x—1 есть частное решение, удовлетворяющее заданным начальным условиям.
Задание 14
Найти общий интеграл уравнения

Решение: Это однородное уравнение, приведем его к виду
т.к. 
Далее вводим новую функцию  , полагая
, полагая 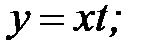 при этом
при этом  и после подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными
и после подстановки данное уравнение преобразуется в уравнение с разделяющимися переменными  или
или 
Разделим переменные:  и, интегрируя, найдем
и, интегрируя, найдем  или
или  . Исключая вспомогательную функцию
. Исключая вспомогательную функцию  , окончательно получим
, окончательно получим 
Задание 15
Решить уравнение 
Решение:
Убедившись, что данное уравнение линейное, полагаем  тогда
тогда  и данное уравнение преобразуется к виду:
и данное уравнение преобразуется к виду:
 или
или 
Так как одну из вспомогательных функций 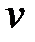 или
или  можно взять произвольно, то выберем в качестве
можно взять произвольно, то выберем в качестве  какой ‑ либо частный интеграл уравнения
какой ‑ либо частный интеграл уравнения  .
.
Тогда для отыскания  получим уравнение:
получим уравнение:  .
.
Решая первое уравнение, найдем  . Разделяя переменные и интегрируя, найдем его простейший, отличный от нуля частный интеграл:
. Разделяя переменные и интегрируя, найдем его простейший, отличный от нуля частный интеграл:

Подставляя v во второе уравнение и решая его, найдем 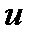 как общий интеграл этого уравнения:
как общий интеграл этого уравнения: 
Зная  и
и  , находим искомую функцию
, находим искомую функцию 
 .
.
Задание 16
Найти частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами, удовлетворяющее начальным условиям:

Решение: Общий вид такого уравнения:  , где
, где  и
и  ‑ действительные числа. Корни его характеристического уравнения
‑ действительные числа. Корни его характеристического уравнения  могут быть:
могут быть:
1) действительными и различными: 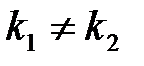 ;
;
2) действительными и равными:  ;
;
3) комплексными:  .
.
Им соответствуют следующие общие решения уравнения:
1)  ;
;
2)  ;
;
3)  .
.
а) Характеристическое уравнение  имеет два различных вещественных корня
имеет два различных вещественных корня  , поэтому общее решение эт
, поэтому общее решение эт