Цель работы
Освоение методов математической обработки результатов исследования свойств текстильных материалов; определение уравнения регрессии по данным однофакторного эксперимента.
Пособия и инструменты: таблицы значений критериев Кочрена, Стьюдента, Фишера; микрокалькулятор.
Содержание работы
1. Статистическая обработка первичных результатов эксперимента.
2. Расчет критерия Кочрена и проверка однородности дисперсии в опытах матрицы.
3. Определение средней дисперсии выходного параметра в опытах матрицы.
4. Определение коэффициентов регрессии и составление уравнения регрессии.
5. Определение адекватности уравнения регрессии. Расчет критерия Фишера.
6. Оценка значимости коэффициентов регрессии.
7. Определение доверительных интервалов средних и индивидуальных значений выходного параметра.
8. Построение графика полученного уравнения регрессии.
9. Анализ результатов работы. Формулировка выводов.
Общие сведения
В настоящее время при исследовании свойств текстильных материалов и других видов продукции широкое применение получили математико-статистические методы планирования экспериментов.
В задачу планирования эксперимента входят: выбор необходимых для эксперимента опытов, т.е. построение матрицы планирования, выбор методов математической обработки результатов эксперимента.
Существует два вида планирования активного эксперимента: традиционное (классическое) однофакторное и многофакторное (факторное).
В традиционном однофакторном планировании изучается влияние на выходной параметр одного входного параметра (фактора).
В результате обработки экспериментальных данных определяют взаимосвязь между выходным параметром (Y) и варьируемым на нескольких уровнях фактором (X). Математическая модель в общем виде описывается функцией отклика:
y = f(x) (1)
При существовании линейной связи между входными и выходными параметрами уравнение регрессии имеет следующий вид:
y = do+d1(x-x̃), (2)
где d0,d1 – коэффициенты уравнения регрессии.
Адекватность уравнения регрессии проверяется по критерию Фишера [1,4]. Если расчетное значение критерия Фишера (Fp) меньше табличного (Fm), то гипотеза об адекватности линейной модели не отвергается.
Выполнение работы
1. Статистическая обработка первичных результатов эксперимента
Полученные значения статистических характеристик заносим в соответствующие графы табл. 1.
Таблица 1
Расчёты статистических характеристик
| № опыта | Фактор Х | Значение параметра,Y | Ỹ | S2 | S | Св | |
| 1. 1 | 9.93 | 9.47 | 9.70 | 0.106 | 0.325 | 3.353 | |
| 2. 2 | 9.81 | 9.32 | 9.56 | 0.120 | 0.346 | 3.622 | |
| 3. 3 | 9.76 | 9.21 | 9.48 | 0.151 | 0.389 | 4.1 | |
| 4. 4 | 9.74 | 9.16 | 9.45 | 0.168 | 0.41 | 4.34 | |
| 5. | 9.73 | 9.12 | 9.42 | 0.186 | 0.431 | 4.577 | |
| 6. | 9.68 | 9.10 | 9.39 | 0.168 | 0.41 | 4.368 | |
| 7. | 9.67 | 9.07 | 9.37 | 0.180 | 0.424 | 4.528 | |
| 8. | 9.64 | 9.04 | 9.34 | 0.180 | 0.424 | 4.542 | |
| 9. | 9.63 | 9.01 | 9.32 | 0.192 | 0.438 | 4.704 | |
| 10. | 9.62 | 9.00 | 9.32 | 0.192 | 0.438 | 4.709 | |
| 11. | 9.61 | 8.99 | 9.30 | 0.192 | 0.438 | 4.714 | |
| 12. | 9.62 | 8.97 | 9.29 | 0.212 | 0.46 | 4.945 | |
| 13. | 9.60 | 8.95 | 9.27 | 0.212 | 0.46 | 4.955 | |
| 14. | 9.58 | 8.94 | 9.26 | 0.205 | 0.453 | 4.887 | |
| 15. | 9.57 | 8.92 | 9.24 | 0.212 | 0.46 | 4.972 | |
| 16. | 9.54 | 8.92 | 9.23 | 0.192 | 0.438 | 4.75 | |
| 17. | 9.55 | 8.93 | 9.22 | 0.192 | 0.438 | 4.745 | |
| 18. | 9.53 | 8.90 | 9.21 | 0.198 | 0.445 | 4.834 | |
| 19. | 9.53 | 8.89 | 9.21 | 0.205 | 0.453 | 4.914 | |
| 20. | 9.52 | 8.88 | 9.20 | 0.205 | 0.453 | 4.919 | |
| 21. | 9.51 | 8.86 | 9.18 | 0.212 | 0.46 | 5.004 | |
| 22. | 9.49 | 8.88 | 9.18 | 0.186 | 0.431 | 4.696 | |
| 23. | 9.49 | 8.85 | 9.17 | 0.205 | 0.453 | 4.935 | |
| 24. | 9.49 | 8.82 | 9.15 | 0.225 | 0.474 | 5.175 | |
| 25. | 9.47 | 8.82 | 9.14 | 0.212 | 0.46 | 5.026 | |
| 26. | 9.46 | 8.82 | 9.14 | 0.205 | 0.453 | 4.951 | |
| 27. | 9.45 | 8.82 | 9.13 | 0.225 | 0.474 | 5.175 | |
| 28. | 9.47 | 8.80 | 9.13 | 0.212 | 0.46 | 5.026 | |
| 29. | 9.46 | 8.80 | 9.13 | 0.218 | 0.467 | 5.112 | |
| 30. | 9.45 | 8.79 | 9.12 | 0.218 | 0.467 | 5.117 |
2. Расчёт критерия Кочрена и проверка однородности дисперсии в опытах матрицы
Для проверки однородности дисперсии и воспроизводимости эксперимента при одинаковой повторности (m) всех опытов рассчитываем значение критерия Кочрена Gp по формуле
(3)
где 
- максимальная дисперсия из всех опытов;
- сумма всех дисперсий эксперимента.
Далее расчётное значение Gp сравниваем с табличным значением GT. Дисперсии однородны и число повторных опытов одинаково, т.к. Gp < GT (0.039<0.3632).
3. Определение средней дисперсии выходного параметра в опытах матрицы
Т.к. в опытах матрицы дисперсии однородны и число повторных опытов одинаково, то среднюю дисперсию определяют по формуле
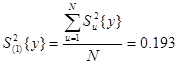(4)
После этого определяем число степеней свободы средней дисперсии;
F(S2(1){y})=N(m-1)=30 (5)
Средняя дисперсия характеризует средний разброс значений выходного параметра относительно его средних значений, т.е. ошибку опытов в эксперименте.
4. Определение коэффициентов регрессии и составление уравнения регрессии
Дисперсии выходного параметра для каждого уровня фактора однородны, следлвательно, применяем метод наименьших квадратов.
Коэффициенты уравнения регрессии определяем по формулам:
(6)
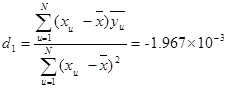(7)
где 
- среднее значение результата эксперимента;
xu - значение фактора на определенном u-уровне;
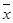- среднее значение фактора.
Для удобства все промежуточные расчеты сводят в табл. 2.
Таблица 2
Расчет коэффициентов уравнения регрессии
| № опыта u | Фактор xu | xu- x̃ | (xu- x̃)2 | Ỹu | (xu- x̃) Ỹu |
| 1. | -110.567 | 12225.06 | 9.70 | -1072.49 | |
| 2. | -102.567 | 10519.99 | 9.56 | -980.54 | |
| 3. | -94.567 | 8942.91 | 9.48 | -896.49 | |
| 4. | -87.567 | 7667.98 | 9.45 | -827.51 | |
| 5. | -79.567 | 6331.38 | 9.42 | -749.52 | |
| 6. | -71.567 | 5121.84 | 9.39 | -672.01 | |
| 7. | -64.567 | 4168.89 | 9.37 | -604.99 | |
| 8. | -56.567 | 3199.83 | 9.34 | -528.34 | |
| 9. | -48.567 | 2358.75 | 9.32 | -452.64 | |
| 10. | -41.567 | 1727.82 | 9.32 | -387.40 | |
| 11. | -33.567 | 1126.74 | 9.30 | -312.17 | |
| 12. | -26.567 | 705.81 | 9.29 | -246.81 | |
| 13. | -18.567 | 344.73 | 9.27 | -172.12 | |
| 14. | -10.567 | 111.66 | 9.26 | -97.85 | |
| 15. | -3.567 | 12.72 | 9.24 | -32.96 | |
| 16. | 4.433 | 19.65 | 9.23 | 40.92 | |
| 17. | 11.433 | 130.71 | 9.22 | 105.41 | |
| 18. | 19.433 | 377.64 | 9.21 | 178.98 | |
| 19. | 26.433 | 698.70 | 9.21 | 243.45 | |
| 20. | 34.433 | 1185.63 | 9.20 | 316.78 | |
| 21. | 41.433 | 1716.69 | 9.18 | 380.35 | |
| 22. | 49.433 | 2443.62 | 9.18 | 453.79 | |
| 23. | 56.433 | 3184.68 | 9.17 | 517.49 | |
| 24. | 64.433 | 4151.61 | 9.15 | 589.56 | |
| 25. | 71.433 | 5102.67 | 9.14 | 652.89 | |
| 26. | 79.433 | 6309.60 | 9.14 | 726.60 | |
| 27. | 86.433 | 7470.66 | 9.13 | 489.13 | |
| 28. | 94.433 | 8917.59 | 9.13 | 862.17 | |
| 29. | 101.433 | 10288.65 | 9.13 | 926.08 | |
| 30. | 109.433 | 11975.58 | 9.12 | 998.02 |
После определения коэффициентов составляют искомое уравнение регрессии:
yR = do+d1(x-x̃). (8)
5. Определение адекватности уравнения регрессии. Расчеты критерия Фишера. Для определения адекватности полученного уравнения (8) используют критерий Фишера, расчетное значение которого определяем по формуле
(9)
где S2(1) – средняя дисперсия или дисперсия воспроизводимости, определяемая но формуле (4);
S2(2) – дисперсия, характеризующая рассеивание средних экспериментальных значений уu относительно прямой линии, определяемой по формуле (8) (дисперсия адекватности).
Дисперсия S2(2) характеризует точность аппроксимации зависимости ỹ=f(X) прямой линией, ее определяют по формуле
(10)
где 
и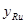 
экспериментальное и расчетное значения выходного параметра.
После этого определяют число степеней свободы дисперсии адекватности
F{S2(2)}=N-2=28 (11)
Далее подставляем в формулу (9) значения дисперсии S2(1){y}и S2(2){y} рассчитывают критерий Фишера. Fp сравниваем с табличным значением критерия Фишера FT, которое определяют из [1.4] при доверительной вероятности α=0,95 и число степеней свободы f {S2(2)} и f { S2(1)}
FT =2.38, а Fр = 0.029
Fр < FT
Т.к. Fр < FT, то линейное уравнение адекватно.
Расчет суммы в формуле (10) сводим в табл. 3. Расчетные значения выходного параметра 
определяем из уравнения (8), подставляя значения Хu.
Таблица 3
Расчёт дисперсии адекватности
| u | xu | d1xu | YRu | ỹu | ỹu- YRu | (ỹu- YRu)2 |
| 1. | -7.864×10-3 | 9.492 | 9.70 | 0.208 | 0.043 | |
| 2. | -0.024 | 9.477 | 9.56 | 0.083 | 6.950×10-3 | |
| 3. | -0.039 | 9.461 | 9.48 | 0.019 | 3.645×10-4 | |
| 4. | -0.053 | 9.447 | 9.45 | 2.853× 10-3 | 8.140×10-6 | |
| 5. | -0.069 | 9.431 | 9.42 | -0.011 | 1.304×10-4 | |
| 6. | -0.085 | 9.416 | 9.39 | -0.026 | 6.601×10-4 | |
| 7. | -0.098 | 9.402 | 9.37 | -0.032 | 1.020×10-3 | |
| 8. | -0.114 | 9.386 | 9.34 | -0.046 | 2.135×10-3 | |
| 9. | -0.130 | 9.370 | 9.32 | -0.050 | 2.548×10-3 | |
| 10. | -0.144 | 9.357 | 9.32 | -0.037 | 1.348×10-3 | |
| 11. | -0.159 | 9.341 | 9.30 | -0.041 | 1.680×10-3 | |
| 12. | -0.173 | 9.327 | 9.29 | -0.037 | 1.386×10-3 | |
| 13. | -0.189 | 9.312 | 9.27 | -0.042 | 1.722×10-3 | |
| 14. | -0.204 | 9.296 | 9.26 | -0.036 | 1.280×10-3 | |
| 15. | -0.218 | 9.282 | 9.24 | -0.042 | 1.765×10-3 | |
| 16. | -0.234 | 9.266 | 9.23 | -0.036 | 1.317×10-3 | |
| 17. | -0.248 | 9.253 | 9.22 | -0.033 | 1.058×10-3 | |
| 18. | -0.263 | 9.237 | 9.21 | -0.027 | 7.180×10-4 | |
| 19. | -0.277 | 9.223 | 9.21 | -0.013 | 1.699×10-4 | |
| 20. | -0.293 | 9.207 | 9.20 | -7.308×10-3 | 5.340×10-5 | |
| 21. | -0.307 | 9.194 | 9.18 | -0.014 | 1.835×10-4 | |
| 22. | -0.322 | 9.178 | 9.18 | 2.181×10-3 | 4.756×10-6 | |
| 23. | -0.336 | 9.164 | 9.17 | 5.942×10-3 | 3.531×10-5 | |
| 24. | -0.352 | 9.148 | 9.15 | 1.669×10-3 | 2.786×10-6 | |
| 25. | -0.366 | 9.135 | 9.14 | 5.430×10-3 | 2.949×10-5 | |
| 26. | -0.381 | 9.119 | 9.14 | 0.021 | 4.476×10-4 | |
| 27. | -0.395 | 9.105 | 9.13 | 0.025 | 6.210×10-4 | |
| 28. | -0.411 | 9.089 | 9.13 | 0.041 | 1.652×10-3 | |
| 29. | -0.425 | 9.076 | 9.13 | 0.054 | 2.960×10-3 | |
| 30. | -0.440 | 9.060 | 9.12 | 0.060 | 3.616×10-3 |
6. Оценка значимости коэффициентов регрессии
Для определения значимости полученных коэффициентов d0 и d1 уравнения (8) используется критерий Стьюдента [1], расчетное значение которого определяем по формуле
tp=|di|/S{di}=3,114 (12)
где S {di} - оценка среднеквадратического отклонения коэффициента регрессии di.
Дисперсию коэффициентов регрессии S2{do} и S2{d1} рассчитываем по формулам:
(13)
(14)
В формулы (13) и (14) входит дисперсия S2{y}, которая является сводной оценкой дисперсии случайной величины Yu выходного параметра при условии линейной связи. Эту дисперсию определяем по формуле
(15)
далее определяют число степеней свободы этой дисперсии:
f{S2}=mN-2=58(16)
Сравниваем табличное и расчётное значения критерия Стьюдента. Если tp>tт, то коэффициенты уравнения регрессии значимы и, следовательно, связь между Y и Х значима.
В нашем случае tр=3,114, а tt=2,0. Следовательно, связь между Y и Х значима.
После этого определяем абсолютные ошибки коэффициентов регрессии ε{di}:
ε {di}=S{di}·tT[α,f{S2}]. (17)
ε {d0}=2,314
ε {d1}=0,035
Тогда для истинных значений коэффициентов регрессии δ0 и δ1в линейном уравнении (8) доверительные интервалы определяются неравенством
di-ε{di}≤ δi≤ds+ ε{di}. (18)
6,961≤ δ0≤5,289
-0,036967≤ δ1≤-0,033
7. Определение доверительных интервалов средних и индивидуальных значений выходного параметра
Чтобы определить степень отклонения расчетных значений выходного параметра YRu от истинного его значения при каждом уровне фактора Xu, определяем доверительные ошибки ε{YRu} расчетного значения выходного параметра и доверительные интервалы средних и индивидуальных значений выходного параметра.
Доверительные ошибки расчетных значений выходного параметра для каждого уровня фактора рассчитывают по формуле
εm{YRu}=Sm{yRu}·tT[α,f{S2}] (19)
где Sm{yRu} – оценка среднеквадратического отклонения расчетного значения выходного параметраYRu для каждого значения xu.
Оценку среднеквадратического отклонения рассчитывают по формуле
(20)
Расчеты εm{YRu} и Sm{YRu} заносим в табл.4.
Далее в таблицу заносят расчетные значения yRu, полученные по уравнению регрессии (8).
Зная ошибки расчетной величины, определяем доверительные интервалы для испытанных средних значений выходного параметра.
Нижний доверительный интервал определяют:
Ym(н)=yRu- εm,(21)
верхний доверительный интервал:
Ym(в)=yRu+ εm, ( 22 )
Значения верхних и нижних значений доверительных интервалов для каждого опыта заносим в табл. 4.
Таблица 4
Доверительные интервалы средних значений
| u | xu | (xu- x̃)2 | Sm2 | Sm | εm | YRu | Ym(н) | Ym(в) |
| 1. | 12225.06 | 4.871e | 0.070 | 8.096 | 9.492 | 1.397 | 17.588 | |
| 2. | 10519.99 | 4.192e | 0.065 | 7.510 | 9.477 | 1.967 | 16.987 | |
| 3. | 8942.91 | 3.563e | 0.060 | 6.924 | 9.461 | 2.537 | 16.385 | |
| 4. | 7667.98 | 3.055e | 0.055 | 6.412 | 9.447 | 3.035 | 15.859 | |
| 5. | 6331.38 | 2.523e | 0.050 | 5.826 | 9.431 | 3.605 | 15.258 | |
| 6. | 5121.84 | 2.041e | 0.045 | 5.241 | 9.416 | 4.175 | 14.656 | |
| 7. | 4168.89 | 1.661e | 0.041 | 4.728 | 9.402 | 4.674 | 14.130 | |
| 8. | 3199.83 | 1.275e | 0.036 | 4.142 | 9.386 | 5.244 | 13.529 | |
| 9. | 2358.75 | 9.401e | 0.031 | 3.557 | 9.370 | 5.814 | 12.927 | |
| 10. | 1727.82 | 6.888e | 0.026 | 3.044 | 9.357 | 6.312 | 12.401 | |
| 11. | 1126.74 | 4.493e | 0.021 | 2.459 | 9.341 | 6.882 | 11.800 | |
| 12. | 705.81 | 2.816e | 0.017 | 1.947 | 9.327 | 7.381 | 11.274 | |
| 13. | 344.73 | 1.377e | 0.012 | 1.361 | 9.312 | 7.950 | 10.673 | |
| 14. | 111.66 | 4.488e | 0.0067 | 0.777 | 9.296 | 8.519 | 10.073 | |
| 15. | 12.72 | 5.467e | 0.002338 | 0.271 | 9.282 | 9.011 | 9.553 | |
| 16. | 19.65 | 8.228e | 0.002868 | 0.333 | 9.266 | 8.934 | 9.599 | |
| 17. | 130.71 | 5.247e | 0.007244 | 0.840 | 9.253 | 8.412 | 10.093 | |
| 18. | 377.64 | 1.509e | 0.012 | 1.425 | 9.237 | 7.812 | 10.662 | |
| 19. | 698.70 | 2.788e | 0.017 | 1.937 | 9.223 | 7.286 | 11.160 | |
| 20. | 1185.63 | 4.728e | 0.022 | 2.522 | 9.207 | 6.685 | 11.729 | |
| 21. | 1716.69 | 6.843e | 0.026 | 3.035 | 9.194 | 6.159 | 12.228 | |
| 22. | 2443.62 | 9.739e | 0.031 | 3.620 | 9.178 | 5.558 | 12.798 | |
| 23. | 3184.68 | 1.269e | 0.036 | 4.133 | 9.164 | 5.031 | 13.297 | |
| 24. | 4151.61 | 1.654e | 0.041 | 4.718 | 9.148 | 4.430 | 13.867 | |
| 25. | 5102.67 | 2.033e | 0.045 | 5.231 | 9.135 | 3.904 | 14.365 | |
| 26. | 6309.60 | 2.514e | 0.050 | 5.816 | 9.119 | 3.302 | 14.935 | |
| 27. | 7470.66 | 2.977e | 0.055 | 6.329 | 9.105 | 2.776 | 15.434 | |
| 28. | 8917.59 | 3.553e | 0.060 | 6.915 | 9.089 | 2.175 | 16.004 | |
| 29. | 10288.65 | 4.099e | 0.064 | 7.427 | 9.076 | 1.648 | 16.503 | |
| 30. | 11975.58 | 4.771e | 0.069 | 8.013 | 9.060 | 1.047 | 17.073 |
Далее определяем границы доверительного интервала для индивидуальных значений выходного параметра Y при каждом уровне фактора.
Верхняя граница интервала:
y l (в)=yRu+S l ·tт[α,f{S2}]. (23)
Нижняя граница интервала:
y l (в)=yRu-S l ·tт[α,f{S2}]. (23)
Предварительно определяем ошибку:
(25)
Используя значения Sm из табл. 4 и ранее определенные по уравнению (15) значения S2{у} и критерий Стьюдента, определяем верхние и нижние границы искомой зоны по формулам (23) и (24), сводя все расчеты в табл. 5,
Таблица 5
| u | xu | Sm2 | S l 2 | S l | YRu | tт· S l | Y l (н) | Y l (в) |
| 1. | 4.871e | 0.107 | 0.328 | 9.492 | 0.656 | 8.837 | 10.148 | |
| 2. | 4.192e | 0.107 | 0.327 | 9.477 | 0.653 | 8.823 | 10.130 | |
| 3. | 3.563e | 0.106 | 0.326 | 9.461 | 0.652 | 8.809 | 10.112 | |
| 4. | 3.055e | 0.106 | 0.325 | 9.447 | 0.650 | 8.797 | 10.097 | |
| 5. | 2.523e | 0.105 | 0.324 | 9.431 | 0.648 | 8.783 | 10.080 | |
| 6. | 2.041e | 0.105 | 0.323 | 9.416 | 0.647 | 8.769 | 10.063 | |
| 7. | 1.661e | 0.104 | 0.323 | 9.402 | 0.646 | 8.756 | 10.048 | |
| 8. | 1.275e | 0.104 | 0.322 | 9.386 | 0.644 | 8.742 | 10.031 | |
| 9. | 9.401e | 0.103 | 0.322 | 9.370 | 0.643 | 8.727 | 10.014 | |
| 10. | 6.888e | 0.103 | 0.321 | 9.357 | 0.643 | 8.714 | 9.999 | |
| 11. | 4.493e | 0.103 | 0.321 | 9.341 | 0.642 | 8.699 | 9.983 | |
| 12. | 2.816e | 0.103 | 0.321 | 9.327 | 0.641 | 8.686 | 9.969 | |
| 13. | 1.377e | 0.103 | 0.320 | 9.312 | 0.641 | 8.671 | 9.952 | |
| 14. | 4.488e | 0.103 | 0.320 | 9.296 | 0.641 | 8.655 | 9.936 | |
| 15. | 5.467e | 0.103 | 0.320 | 9.282 | 0.640 | 8.642 | 9.923 | |
| 16. | 8.228e | 0.103 | 0.320 | 9.266 | 0.640 | 8.626 | 9.907 | |
| 17. | 5.247e | 0.103 | 0.320 | 9.253 | 0.641 | 8.612 | 9.893 | |
| 18. | 1.509e | 0.103 | 0.320 | 9.237 | 0.641 | 8.596 | 9.878 | |
| 19. | 2.788e | 0.103 | 0.321 | 9.223 | 0.641 | 8.582 | 9.864 | |
| 20. | 4.728e | 0.103 | 0.321 | 9.207 | 0.642 | 8.565 | 9.849 | |
| 21. | 6.843e | 0.103 | 0.321 | 9.194 | 0.643 | 8.551 | 9.836 | |
| 22. | 9.739e | 0.104 | 0.322 | 9.178 | 0.644 | 8.534 | 9.821 | |
| 23. | 1.269e | 0.104 | 0.322 | 9.164 | 0.644 | 8.520 | 9.808 | |
| 24. | 1.654e | 0.104 | 0.323 | 9.148 | 0.646 | 8.503 | 9.794 | |
| 25. | 2.033e | 0.105 | 0.323 | 9.135 | 0.647 | 8.488 | 9.781 | |
| 26. | 2.514e | 0.105 | 0.324 | 9.119 | 0.648 | 8.471 | 9.767 | |
| 27. | 2.977e | 0.106 | 0.325 | 9.105 | 0.650 | 8.455 | 9.755 | |
| 28. | 3.553e | 0.106 | 0.326 | 9.089 | 0.651 | 8.438 | 9.741 | |
| 29. | 4.099e | 0.107 | 0.327 | 9.076 | 0.653 | 8.422 | 9.729 | |
| 30. | 4.771e | 0.107 | 0.328 | 9.060 | 0.655 | 8.405 | 9.715 |
Выводы: в процессе выполнения лабораторной работы были изучены методы математической обработки результатов исследования свойств текстильных материалов, приведён расчёт критерия Кочрена и проверка однородности дисперсии в опытах матрицы, определена средняя дисперсия выходного параметра в опытах матрицы, коэффициенты регрессии, адекватность уравнения регрессии, расчёт критерия Фишера, определены уравнения регрессии по данным однофакторного эксперимента, доверительные интервалы средних и индивидуальных значений выходного параметра, построен график полученного уравнения регрессии.