Лекция 4.
Закон распределения функции от случайного вектора.
1. Если случайный вектор  имеет плотность
имеет плотность  , а
, а  - скалярная функция двух переменных, то функция распределения
- скалярная функция двух переменных, то функция распределения 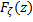 находится по формуле
находится по формуле  .
.
2. В частности, если 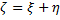 , то
, то
 .
.
3. Если же случайные величины  и
и  независимы, то
независимы, то

Эту формулу называют формулой композиции двух распределений или формулой свертки.
Доказательство.
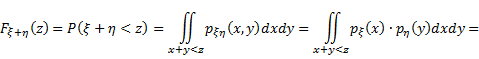

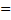
 , откуда
, откуда
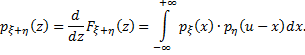
Мораль. Плотность суммы независимых случайных величин равна свертке плотностей слагаемых.
Пример 1. Независимые СВ  и
и  имеют равномерное распределение на
имеют равномерное распределение на  . Найдите плотность распределения случайной величины
. Найдите плотность распределения случайной величины 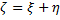 .
.
Решение. Плотности распределения вероятностей  и
и  равны
равны
 . Пусть - плотность распределения суммы
. Пусть - плотность распределения суммы  .
.
Получим:

Если 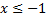 , то отрезок
, то отрезок  лежит левее отрезка
лежит левее отрезка  , поэтому
, поэтому
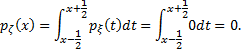 Если
Если 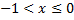 , то
, то  ,
,  поэтому
поэтому
 Если
Если  , то
, то  ,
, 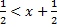 поэтому
поэтому
 Если
Если  , то отрезок
, то отрезок  лежит правее отрезка
лежит правее отрезка  , поэтому
, поэтому
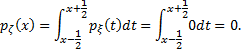 В итоге получаем
В итоге получаем  .
.
Распределение с плотностью 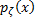 называется треугольным распределением на отрезке [-1;1] или распределением Симпсона.
называется треугольным распределением на отрезке [-1;1] или распределением Симпсона.
Свойства математического ожидания и дисперсии.
1. 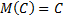 .
.
2.  .
.
3.  .
.
4.  , если
, если  независимы.
независимы.
5. 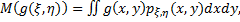 в частности,
в частности,
 ,
,
 .
.
6. 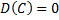 .
.
7.  .
.
8.  ,
,
где 
в частности,  если
если  независимы
независимы 
Доказательство. 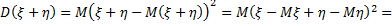

Многомерный нормальный вектор и его свойства
Определение. Нормальным случайным вектором называется случайный вектор 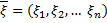 , имеющий плотность распределения вида
, имеющий плотность распределения вида
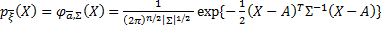 ,
,
где 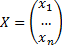 - столбец переменных,
- столбец переменных,
 – координаты постоянного вектора
– координаты постоянного вектора  ,
,
 – невырожденная положительно определенная симметричная матрица.
– невырожденная положительно определенная симметричная матрица.
Замечание. Выражение  в показателе экспоненты представляет собой положительно определенную квадратичную форму от
в показателе экспоненты представляет собой положительно определенную квадратичную форму от  переменных.
переменных.
В частности для  плотность зависит от пяти параметров:
плотность зависит от пяти параметров: 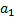 ,
,  ,
,  ,
,  ,
,  .
.
Положительная определенность матрицы означает, что 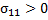 ,
,  ,
,
 .
.
Тогда 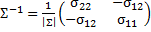 , и плотность примет вид
, и плотность примет вид
 .
.
Вид графика функции показан на рисунке.

Свойства нормального вектора ( 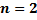 ).
).
1. Распределения компонент нормального вектора нормальны, причем  ,
,  .
.
2.  ,
,  .
.
3. 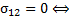
 и
и  независимы. То есть для нормальных случайных величин некоррелируемость эквивалентна независимости.
независимы. То есть для нормальных случайных величин некоррелируемость эквивалентна независимости.
4. Если  – нормальный случайный вектор, то распределения случайной величины
– нормальный случайный вектор, то распределения случайной величины 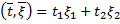 нормальное (или вырожденное) для произвольного
нормальное (или вырожденное) для произвольного  .
.
(Обратное утверждение тоже верно: если для произвольного постоянного вектора  распределение случайной величины
распределение случайной величины 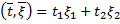 нормальное (или вырожденное), то
нормальное (или вырожденное), то  – нормальный случайный вектор.)
– нормальный случайный вектор.)
Пример 2. Пусть дан нормальный случайный вектор  с параметрами
с параметрами
 ,
,  ,
,  ,
,  ,
,  .
.
Решение. Найдем закон распределения 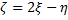 . Согласно доказанному свойству, распределение
. Согласно доказанному свойству, распределение  нормально. Найдем параметры, используя свойства математического ожидания и дисперсии.
нормально. Найдем параметры, используя свойства математического ожидания и дисперсии.
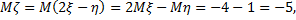

 .
.
Выпишем плотность: 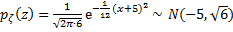 .
. 
Рассмотрим двумерный вектор  с зависимыми компонентами. Как мы уже знаем, коэффициент корреляции не характеризует в полной мере зависимость между компонентами.
с зависимыми компонентами. Как мы уже знаем, коэффициент корреляции не характеризует в полной мере зависимость между компонентами.
Определение. Условной функцией распределения случайной величины  при условии, что СВ
при условии, что СВ  попала в полуинтервал
попала в полуинтервал 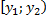 называется условная вероятность
называется условная вероятность
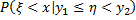 .
.
Таким образом,  . (1)
. (1)
 Если
Если  – непрерывный случайный вектор, то обе вероятности в формуле (1) можно выразить через плотность вероятности случайного вектора
– непрерывный случайный вектор, то обе вероятности в формуле (1) можно выразить через плотность вероятности случайного вектора  Совместное выполнение неравенств
Совместное выполнение неравенств 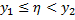 и
и 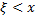 соответствует попаданию случайной точки
соответствует попаданию случайной точки  в половину полосы (см. рис.). Поэтому, по формуле для функции распределения двумерного случайного вектора получим:
в половину полосы (см. рис.). Поэтому, по формуле для функции распределения двумерного случайного вектора получим:
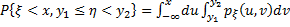 (2)
(2)
Вероятность в знаменателе правой части формулы (1) выражается через плотность вероятности одной СВ  :
:
 (3)
(3)
Подставляя выражения (2) и (3) в формулу (1) получим:
 (4)
(4)
Дифференцируя формулу (4) по  можно найти условную плотность СВ
можно найти условную плотность СВ  при условии, что СВ
при условии, что СВ  принимает значение, заключенное в пределах
принимает значение, заключенное в пределах 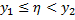 :
:
 (5)
(5)
Если в формуле (5) положить  ,
, 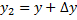 и перейти к пределу при
и перейти к пределу при 
 , считая функции
, считая функции  и
и  непрерывными по
непрерывными по  в интервале
в интервале  , то можно найти условный закон распределения СВ
, то можно найти условный закон распределения СВ  при данном значении СВ
при данном значении СВ  (он имеет наибольшее практическое применение среди всех условных ЗР СВ
(он имеет наибольшее практическое применение среди всех условных ЗР СВ  , соответствующих различным значениям
, соответствующих различным значениям  и
и  ). Для этого применим к интегралам в числителе и знаменателе теорему о среднем. После сокращения на
). Для этого применим к интегралам в числителе и знаменателе теорему о среднем. После сокращения на  получаем
получаем  , где
, где  и
и  – некоторые числа, заключенные между нулем и единицей. Переходим к пределу при
– некоторые числа, заключенные между нулем и единицей. Переходим к пределу при 
 . Обозначив условную плотность вероятности СВ
. Обозначив условную плотность вероятности СВ  относительно СВ
относительно СВ  через
через 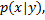 получим
получим
 (6)
(6)
Аналогично для условной плотности вероятности СВ  относительно СВ
относительно СВ  имеем:
имеем:
 (7)
(7)
Равенства (6) и (7) можно переписать в виде  .
.
Мы получили теорему умножения плотностей вероятностей: совместная плотность вероятности двух СВ равна плотности вероятности одной из них, умноженной на условную плотность вероятности другой, относительно первой.
Замечание. Из теоремы умножения можно заключить, что необходимым и достаточным условием независимости СВ  и
и  является равенство
является равенство  при всех значениях
при всех значениях  или
или  при всех
при всех  .
.
Определение. Условным математическим ожиданием одной из СВ, входящих в систему  называется математическое ожидание, вычисляемое при условии, что другая СВ приняла определенное значение (или попала в данный интервал).
называется математическое ожидание, вычисляемое при условии, что другая СВ приняла определенное значение (или попала в данный интервал).
Обозначение  ] или
] или  и
и 
Для непрерывных СВ условные м.о. вычисляются по формулам:
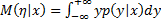 ,
,  , (8)
, (8)
где 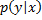 и
и  - условные плотности распределений СВ
- условные плотности распределений СВ  и
и  .
.
Определение. Условное м. о. СВ  при заданном
при заданном  , т.е.
, т.е.  называется функцией регрессии или просто регрессией
называется функцией регрессии или просто регрессией  на
на  (или
(или  по
по  ).
).
Аналогично,  – регрессия
– регрессия  на
на  (или
(или  по
по  ).
).
Графики этих функций называются линиями (или «кривыми») регрессии  на
на  и
и  на
на  соответственно.
соответственно.
Определение. Если обе функции регрессии  на
на  и
и  на
на  линейны, то говорят, что СВ
линейны, то говорят, что СВ  и
и  связаны линейной корреляционной зависимостью.
связаны линейной корреляционной зависимостью.
Пример 3. Координаты случайной точки на плоскости подчиняются нормальному закону распределения 
Определите: а) плотность вероятности компонент  и
и  ; б) условные плотности вероятности
; б) условные плотности вероятности  и
и  ; в) условные математические ожидания; г) условные дисперсии.
; в) условные математические ожидания; г) условные дисперсии.
Решение. а) Для плотности вероятности координаты  имеем
имеем 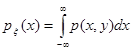
Производя замену переменных 
и учитывая, что 
получим 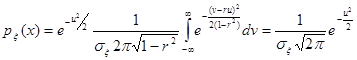 или
или 
Аналогично, находим 
б) Разделим 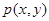 на
на 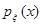 , получим
, получим 
и, аналогично,  .
.
в) Из выражений для условных плотностей вероятности следует, что условное математическое ожидание СВ  при фиксированном значении
при фиксированном значении  , равно
, равно  . Аналогично,
. Аналогично, 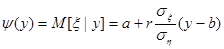 .
.
Замечани е. Обе функции регрессии оказались линейными. Таким образом установлена теорема о нормальной корреляции: если двумерная СВ  распределена по нормальному закону, то СВ
распределена по нормальному закону, то СВ  и
и  связаны линейной корреляционной зависимостью.
связаны линейной корреляционной зависимостью.
Приложение. Доказательство свойств нормального вектора.
1. Распределения компонент нормального вектора нормальны, причем  ,
,  .
.
Доказательство. По общей формуле 
Перед интегрированием преобразуем показатель экспоненты, выделив полный квадрат:


 .
.
Тогда, обозначив  , получим
, получим  , и следовательно
, и следовательно
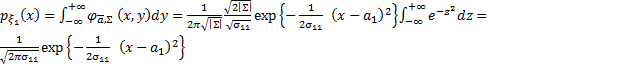 .
.
2.  ,
,  .
.
Доказательство. 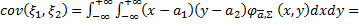



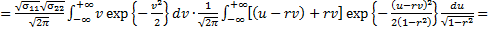

3. 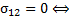
 и
и  независимы.
независимы.
Доказательство.
Если  , то
, то  , откуда
, откуда
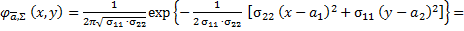

=  .
.
То есть  и
и  независимы.
независимы.
Обратно, если нормально распределенные случайные величины  и
и  независимы, то их совместная плотность
независимы, то их совместная плотность 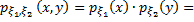
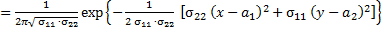 ,
,
что соответствует нормально распределенному вектору с матрицей  ,
,  поскольку в этом случае
поскольку в этом случае 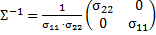 .
.
4. Если  – нормальный случайный вектор, то распределения случайной величины
– нормальный случайный вектор, то распределения случайной величины 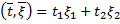 нормальное (или вырожденное) для произвольного
нормальное (или вырожденное) для произвольного  .
.
(Обратное утверждение тоже верно: если для произвольного постоянного вектора  распределение случайной величины
распределение случайной величины 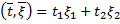 нормальное (или вырожденное), то
нормальное (или вырожденное), то  – нормальный случайный вектор.)
– нормальный случайный вектор.)
Доказательство.
1) Запишем плотность нормального случайного вектора в виде
 и рассмотрим центрированный случайный вектор
и рассмотрим центрированный случайный вектор 
 ,
,  .
.
Поскольку функция распределения центрированного вектора
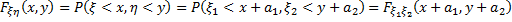 ,
,
то его плотность останется нормальной с той же ковариационной матрицей и нулевым вектором средних значений:
 .
.
2) Рассмотрим функцию распределения случайной величины  и докажем, что ее плотность нормальна.
и докажем, что ее плотность нормальна.


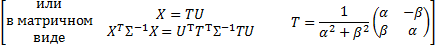
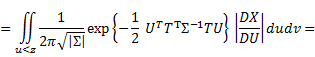


Тогда  .
.
3) Заметим, наконец, что линейная комбинация компонент исходного вектора 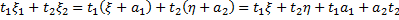 отличается от линейной комбинации вида
отличается от линейной комбинации вида  на постоянное слагаемое, то есть ее распределение также нормально.
на постоянное слагаемое, то есть ее распределение также нормально.