Дифракция Фраунгофера на щели и решетке.

 

Этот тип дифракции реализуется при условии, что размеры щели a много меньше произведения расстояния от источника до щели l на длину волны λ:

 

. (3.1)

 

Рис. 3.4

 

В частности, такой тип дифракции будет наблюдаться в параллельных лучах.

Ход лучей при дифракции на щели объясняет рисунок 3.5. Из этого рисунка следует, что разность хода

 

,

 

где а - ширина щели, j - угол дифракции.

Условие существования этого типа дифракции (3.1) позволяет рассчитать число зон Френеля, укладывающихся на щели:

 

 

 

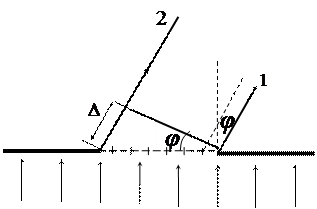Рис. 3.5

 

Как показывает оценочный расчет при реальных значениях a и l для видимого света с длиной волны λ, числовые значения k не очень велики. Но если

 

 

т.е. на разности хода укладывается четное число зон Френеля, то в направлении j наблюдается min.

Поэтому условие min:

А условие max:

 

При φ = 0 будет наблюдаться max, т.к. действует одна зона Френеля.

Распределение интенсивности на экране при дифракции на щели будет выглядеть следующим образом (рис.3.6):

 

 

Рис. 3.6

 

При этом отношение интенсивностей в максимумах будет:

 

 

 

 

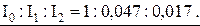
При дифракции на решетке разность хода определяется через период решетки d (см. рис.3.7). При этом

 

d = a + b,

 

где а – ширина щели, а b – расстояние между щелями.

 

Рис. 3.7

 

Кроме того, d = 1/ n, где n - число штрихов на единицу длины решетки (n = N/L), N – общее число штрихов решетки.

 

 

Главные min при дифракции на решетке возникают при условии:

 

, при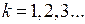

 

При этом взаимная интерференция лучей дает дополнительные min:

 

 

Главные max возникают при условии:

 

 

При N щелях условие дополнительных min будет выглядеть следующим образом:

 

 

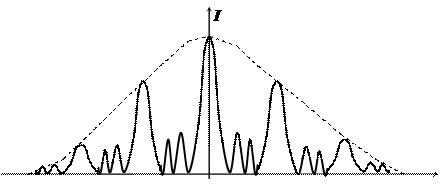
Следовательно, между двумя главными max располагается N – 1 дополнительных min, разделенных вторичными max. При этом чем больше N, тем более острыми будут max. На рисунке 3.8 представлен случай для N = 4.

 

 

 

 

	x

 

Рис. 3.8

 

Так как положение максимумов и минимумов в картине дифракции от дифракционной решетки зависит от длины волны, то дифракционная решетка будет являться спектральным прибором. При этом (как показывает вывод) разрешающая способность решетки равна:

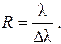
Дифракция также возможна от пространственной решетки кристалла. При этом для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка величины, что и длина волны.

Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную решетки порядка нескольких нанометров. Поэтому наблюдение дифракционной картины возможно на кристаллах, если в качестве излучения использовать рентгеновское излучение с длиной волны l = 0,01 – 10 нм.

Метод расчета дифракции рентгеновских лучей был предложен независимо Г.В. Вульфом¹ и Г. и Л. Брэггами². Они показали, что дифракция рентгеновских лучей является результатом их отражения от системы параллельных кристаллографических плоскостей. Пучок рентгеновских лучей падает под углом скольжения J (см. рис. 3.9) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн.

Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе.

Поэтому будет справедлива формула Вульфа-Брэггов:

 

 

J J · · · · · · d J J · · · · · · dsinJ · · · · · ·

 

 

Рис. 3.9

Следовательно, при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн l, будут наблюдаться дифракционные максимумы.

Этот тип дифракции широко используется в кристаллофизике для двух типов анализов: рентгеноструктурного (нахождение межплоскостного расстояния d по измеренным J и k) и рентгеноспектрального (нахождение l при известном d по измеренным J и k).

 

Г.В. Вульф (1863 – 1925), российский ученый.

² Г. Брэгг (отец, 1862 – 1942) и Л. Брэгг (сын, 1890 – 1971), английские физики.