Лекция 3. Дифракция света
План лекции
3.1. Принцип Гюйгенса-Френеля. Метод зон Френеля.
3.2. Дифракция Френеля на круглом отверстии и диске.
3.3. Дифракция Фраунгофера на щели и решетке.
3.4. Рентгеноструктурные методы исследования строительных материалов.
Принцип Гюйгенса-Френеля. Метод зон Френеля.
Дифракцией называется отклонение волн от прямолинейного распространения, когда волны, огибая препятствия, заходят в область геометрической тени.
Дифракция света - частный случай дифракции волн. Она проявляется в чередующихся max и min интенсивности, когда фронт световой волны частично экранирован.
Как показывают эксперименты и расчеты, условием получения дифракции света с длиной волны λ от препятствия (или отверстия) размером b, находящегося на расстоянии l от источника, являются соотношения:
Поэтому различают два типа дифракции света:
1) дифракция Френеля – дифракция в сходящихся световых пучках, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, т.е. когда b 2~ l λ;
2) дифракция Фраунгофера 1 – дифракция в параллельных лучах, когда источник света и экран расположены далеко один от другого, т.е. когда b 2 << l λ.
Направление распространения волнового фронта можно объяснить по принципу Гюйгенса 2, который устанавливает способ построения фронта волны в момент времени t + Dt по известному положению фронта в момент времени t (см. рис. 3.1).
|
|
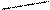
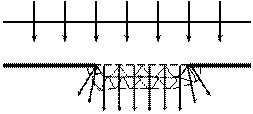
Рис. 3.1
И. Фраунгофер (1787 – 1826), немецкий физик.
2 Х. Гюйгенс (1629 – 1695), нидерландский ученый
Принцип Гюйгенса гласит: каждая точка, до которой доходит волна (в момент времени t), служит центром вторичных волн, огибающая которых дает положение волнового фронта в следующий момент времени (t + Δt).
Однако, принцип Гюйгенса, являясь чисто геометрическим способом построения волновых поверхностей, не затрагивает по существу вопроса об амплитуде, а, следовательно, и об интенсивности волн, распространяющихся по разным направлениям.
Френель вложил в принцип Гюйгенса физический смысл, дополнив его интерференцией вторичных волн.
Принцип Гюйгенса-Френеля гласит: световая волна, возбуждаемая каким либо источником S, может быть представлена как результат суперпозиции (интерференции) вторичных когерентных световых волн, «излучаемых» фиктивными источниками. Такими источниками могут служить физически бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве такой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно.
Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и экраном находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии – такая же, как при отсутствии экрана.
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства.
Используя принцип Гюйгенса-Френеля для вторичных волн можно рассчитать результирующую амплитуду световой волны, учитывая фазы интерферирующих волн.
Однако проще это сделать по методу зон Френеля (см. рис. 3.2). Найдем в произвольной точке P экрана амплитуду световой волны, распространяющейся в однородной среде из точечного источника S. Согласно принципу Гюйгенса-Френеля заменим действие источника S действием воображаемых источников, расположенных на воображаемой поверхности Ф, являющейся поверхностью фронта волны, идущей из S.
 |
Рис. 3.2
Согласно методу зон Френеля, на волновой поверхности Ф (радиуса a) проводятся из точки Р экрана кольцевые зоны, отличающиеся по радиусу r на величину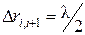 
.
При этом площади каждой зоны будут примерно одинаковы:
а, следовательно, будут практически равны и амплитуды световых колебаний в точке экрана Р, т.е.
.
Т.к. колебания от соседних зон проходят расстояния до экрана, отличающиеся на λ/2, то они приходят в точку наблюдения Р в противофазе. Значит амплитуда результирующего светового колебания в точке Р будет:
где i - число зон (номер последней зоны).
Число зон на полусфере будет
При а = r = 10 см и λ = 0,5 мкм: 
, т. е. N очень велико.
Следовательно, для открытого фронта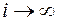 
, т.е.
Но т.к. 
, то
,
т.е.
и 
.
Тогда
,
т.е. действие всей волны сводится к действию половины амплитуды первой зоны Френеля. Этим объясняется прямолинейность распространения света.
Доказательством правомерности деления волнового фронта на зоны Френеля служат так называемые зонные пластинки – стеклянные пластинки, состоящие из концентрических чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля. Такая пластинка, расположенная на соответствующих расстояниях от источника света и от экрана, перекроет, например, четные зоны и оставит неперекрытыми нечетные зоны. В результате этого результирующая амплитуда А = А1 + А3 + А5 +… должна быть больше, чем при полностью открытом фронте. В экспериментах зонная пластинка во много раз увеличивает интенсивность света в точке М.