Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Магнитогорский государственный технический университет
Им. Г.И. Носова»
КАФЕДРА МЕХАНИКИ
Е.В. Куликова
В.И. Кадошников
М.В Андросенко
Кинематический анализ механизмов и машин
Учебно-методическое пособие для студентов технических направлений подготовки и специальностей всех форм обучения
Магнитогорск 2016
Составители: Е.В. Куликова,
М.В Андросенко
Кинематический анализ механизмов и машин: методическое пособие к практическим занятиям по дисциплине «Теория механизмов и машин» для студентов обучающихся по направлению: 151000.62, 150700.62, 151900.62, 190600.62, 190100.62 всех форм обучения. Магнитогорск: ГОУ ВПО «МГТУ им. Г.И. Носова», 2015. 41с.
Рецензент: Зав. каф ТМ и СМ, к.т.н., доцент Савинов А.С.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1
Кинематический анализ кривошипно-ползунных механизмов
Цель: нахождение положений, скоростей и ускорений отдельных точек звеньев, а также угловых скоростей и ускорений звеньев независимо от сил действующих на них [1,2].
Кинематический анализ кривошипно-ползунного механизма показан на рис. 1.1.
В основе кинематического анализа лежат две формулы для определения скорости и ускорения ползуна В.
(1.1)
Где V a - скорость тачки А, лежащей на кривошипе, м/с;
V ab – скорость точки B относительно точки А, м/с;
V b – скорость точки В, принадлежащей ползуну.
Скорость точки А найдем по формуле:
(1.2)
Где w 1 – угловая скорость первого звена, рад/с;
l oa – длина первого звена, м;
(1.3)
Где 
– нормальная составляющая ускорения точки А, м/ 
;
– касательная составляющая ускорения точки А, м/ ;
– нормальная составляющая ускорения точки В относительно точки А, м/ ;
– касательная составляющая ускорения точки В относительно точки А, м/ .
Касательная, составляющая ускорения точки А является производной от угловой скорости первого звена по времени. А угловая скорость является величиной постоянной. Следовательно, 
= 0 и уравнение (1.3) перепишется в следующем виде:
Рис. 1.1 Кинематический анализ кривошипно-ползунного механизма: а – кинематическая схема механизма; б – план скоростей; в – план ускорений.
(1.4)
Ускорения и найдем по следующим формулам:
(1.5)
(1.6)
Где 
рад/с;
, м;
(1.7)
ПОРЯДОК КИНЕМАТИЧЕСКОГО АНАЛИЗА
1.1 Начертить кинематическую схему механизма в масштабе 
.
1) Построить станину 0.
2) Построить горизонтальную ось вращения 4 кривошипа 1.
3) Из точки 0 построить кривошип 1 под углом 
к оси вращения кривошипа. Конец кривошипа обозначить буквой А.
4) Определить масштаб длин 
по формуле
(1.8)
Где 
– произвольно построенная длина отрезка ОА, мм;
– истинная длина кривошипа ОА, м.
5) В соответствии с масштабом построить ось перемещения 5 ползуна 3 на расстоянии 
, которую необходимо отложить на кинематической схеме, найдем по формуле
(1.9)
Где α– истинная длина смещения,α- заданная условием, м;µ1– масштаб длин, мм/м.
Если смещение положительно, то ось перемещения ползуна находится выше оси вращения кривошипа, если отрицательно, то ниже.
6) Из точки А построить шатун 2 длиной 
до пересечения с осью перемещения ползуна.
(1.10)
Где 
– истинная длина шатуна АВ, м.
В точке В будет находится ползун 3.
1.2. Построить план скоростей в масштабе 
.
1) Выбрать полюс Р.
2) Построить вектор скорости точки А. Направление вектора перпендикулярно звену ОА по направлению 
, а длина произвольна в пределах 40-60 мм. Конец вектора обозначить буквой a.
3) Определить масштаб плана скоростей 
по формуле
(1.11)
Где 
– длина произвольно построенного отрезка, соответствующего вектору скорости 
, мм;
– значение скорости точки А, м/с.
4) Построить линию действия скорости точки В относительно точки А. Направлена линия действия перпендикулярно звену АВ и проходит через точку а плана скоростей.
5) Построить линию действия скорости точки В. Направлена линия действия параллельно линии перемещения ползуна и проходит через полюс р.
6) Обозначить точку пересечения линий действия скоростей точки В и точки В относительно точки А буквой b. В результате образовалось два вектора. Первый вектор имеет начало в полюсе р и конец в точке b плана скоростей. Это вектор скорости точки В. Второй вектор имеет начало в точке а и конец в точке b плана скоростей. Это вектор скорости точки В относительно А.
7) Обозначить на векторе ab плана скоростей точку 
– центр тяжести звена АВ на расстоянии 1/3 отрезка ab ближе к точке а. Соединить полюс р с точкой . В результате образовался вектор скорости точки , начало которого в полюсе р и конец в точке .
8) Определить истинные значения скоростей 
, 
, 
. Для этого необходимо измерить соответствующие вектора и разделить измеренные величины на значение масштаба .
1.3 Построить план ускорений в масштабе 
.
1) Выбрать полюс 
.
2) Построить вектор ускорения точки А. Направление вектора параллельно звену ОА от точки А к точке 0, т.е. к центру вращения кривошипа, а длина произвольна в пределах 40-60 мм. Конец вектора обозначить буквой a.
3) Определить масштаб плана скоростей по формуле
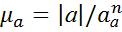(1.12)
Где 
– длина произвольно построенного отрезка, соответствующего вектору скорости , мм;
– значение ускорения точки А, м/
4) Построить нормальную составляющую вектора ускорения точки В относительно точки А. Направление вектора параллельно звену АВ от точки В к точке А по кинематической схеме. Длина вектора строится в соответствии с масштабом 
.
Для этого значение вектора 
необходимо умножить на значение масштаба. Вектор имеет начало в точке а, а его конец обозначим 
.
5) Построить линию действия ускорения точки В относительно точки А касательное. Направлена линия действия перпендикулярно нормальной составляющей и проходит через точку b.
6) Построить линию действия ускорения точки В. Направлена линия действия параллельно линии перемещения ползуна и проходит через полюс .
7) Обозначить точку пересечения линий действия ускорений точки В и точки В относительно точки А касательное буквой b. В результате образовалось два вектора. Первый вектор имеет начало в полюсе и конец в точке b плана ускорений. Это вектор ускорений точки В. Второй вектор имеет начало в точке 
и конец в точке b плана ускорений. Это вектор скорости точки В относительно А касательное.
8) Соединить точку а и точку b плана ускорений. Это будет вектор полного ускорения точки B относительно точки А. Вектор имеет начало в точке а и конец в точке b плана ускорений.
9) Обозначить на векторе ab плана ускорений точку – центр масс звена АВ на расстоянии 1/3 отрезка ab ближе к точке а. Соединить полюс с точкой . В результате образовался вектор ускорения точки , начало которого в полюсе и конец в точке .
10) Определить истинные значения ускорений 
, 
, 
, . Для этого необходимо измерить соответствующие вектора и разделить измеренное значение масштаба .
1.4 Варианты заданий для кинематического анализа кривошипно-ползунного механизма (рис. 1.1, а) сведены в табл. 1.1
Таблица 1.1
| Номер варианта | , м
|  , м
|  , м
| , град
| , рад/с
|
| 1,0 0,9 0,8 0,7 0,6 0,5 -0,6 -0,7 -0,8 -0,9 -1,0 0,9 0,8 0,7 -0,6 -0,5 0,4 -0,5 -0,6 -0,7 | 2,0 1,4 1,1 1,2 0,8 1,0 2,0 0,5 0,8 1,4 1,2 1,4 1,1 0,8 0,6 0,5 0,2 1,0 1,4 2,0 | 5,0 3,5 2,6 3,0 3,5 3,0 4,2 4,5 2,0 3,5 3,0 3,2 4,1 2,5 2,0 1,5 3,0 2,1 3,5 5,5 |
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2