Механизмов
Цель:
1) Определение сил, действующих на звенья механизма.
2) Определение реакций в кинематических парах.
3) Определение уравновешивающего момента.
Порядок силового расчёта кривошипно-ползунного механизма показан на рис. 3.1.
Порядок силового расчета кривошипно-ползунного механизма
1. Начертить кинематическую схему механизма в масштабе 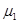 .
.
2. Построить план скоростей в масштабе 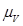
3. Построить план ускорений в масштабе  .
.
4. Выделить структурную группу Ассура и показать все силы, действующее на неё, а также момент инерции второго звена. Момент инерции 2 звена направлен против углового ускорения 2 звена, которое совпадает с направлением касательного ускорения 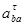 .
.
5. Графо-аналитическим методом решить систему:
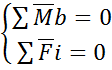 (3.1)
(3.1)
Первое уравнение системы (3.1) как сумму моментов всех сил
относительно точки В, причём знак момента силы считать положительным, если он направлен против часовой стрелки, можно расписать следующим образом:
 (3.2)
(3.2)
Где 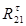 - касательная составляющая силы взаимодействия второго и первого звена, Н;
- касательная составляющая силы взаимодействия второго и первого звена, Н;
 - сила инерции второго звена, Н;
- сила инерции второго звена, Н;
 - сила тяжести второго звена, Н;
- сила тяжести второго звена, Н;
 - момент инерции второго звена, Н∙м;
- момент инерции второго звена, Н∙м;
a – плечо от точки В до действия силы 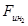 , м;
, м;
b – плечо от точки В до действия силы  , м.
, м.
Плечом по линии действия силы является кратчайшее расстояние или перпендикуляр.
Моменты от сил, которые показаны на рис.2.1.4, но не вошедшие в уравнение (3.2), равны нулю, т.к. линии действия этих сил проходят через точку В.
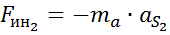 (3.3)
(3.3)
Где 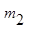 - масса второго звена, кг;
- масса второго звена, кг;
 - ускорение центра тяжести второго звена, м∕с.
- ускорение центра тяжести второго звена, м∕с.
Знак минус в уравнении (3.3) говорит о том, что сила инерции направлена против ускорения.
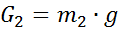 (3.4)
(3.4)
Где g – ускорение свободного падения, равное 9,81  .
.
 (3.5)
(3.5)
Где  - угловое ускорение второго звена,
- угловое ускорение второго звена, 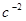 ;
;
 - момент инерции второго звена относительно центра масс,
- момент инерции второго звена относительно центра масс,  .
.
Знак минус в уравнении (3.5) показывает, что момент инерции  направлен против углового ускорения.
направлен против углового ускорения.
 (3.6)
(3.6)
Где 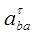 - касательная составляющая ускорения точки В относительно точки А,
- касательная составляющая ускорения точки В относительно точки А, 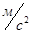 ;
;


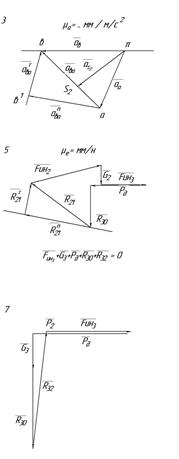

Рис. 3.1 Силовой расчёт кривошипно-ползунного механизма
 - длина звена АВ, м.
- длина звена АВ, м.
Неизвестную силу  найдём из уравнения (3.2).
найдём из уравнения (3.2).
Распишем второе уравнение системы (3.1) как сумму главных векторов всех сил, действующих на структурную группу. Причём неизвестные силы запишем в конце уравнения.
 (3.7)
(3.7)
Где 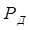 - движущая сила, Н;
- движущая сила, Н;
 - реакция опоры, Н;
- реакция опоры, Н;
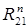 - нормальная составляющая силы взаимодействия второго и первого звена, Н.
- нормальная составляющая силы взаимодействия второго и первого звена, Н.
Для нахождения неизвестных сил 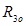 и
и 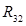 построить план сил:
построить план сил:
1.Выбрать полюс Р1.
Из полюса построить вектор 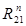 . Направление вектора соответствует показанному на рис.3.1.4. Длина вектора строится произвольно, а конец обозначить r/
. Направление вектора соответствует показанному на рис.3.1.4. Длина вектора строится произвольно, а конец обозначить r/
2.Определить масштаб векторной диаграммы  по методике, описанной в практическом занятии 1.
по методике, описанной в практическом занятии 1.
3.В соответствии с масштабом построить остальные вектора известных сил по направлениям, соответствующим показанным на рис.3.1.4.
4.Построить линию действия вектора 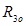 , которая проходит через конец последнего вектора
, которая проходит через конец последнего вектора  диаграммы.
диаграммы.
5.Построить линию действия вектора 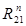 , которая проходит через полюс Р.
, которая проходит через полюс Р.
Пересечение линий действия приведёт к образованию двух векторов.
Первый вектор 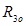 имеет начало в конце вектора
имеет начало в конце вектора  , а конец в точке пересечения линий действия. Второй -
, а конец в точке пересечения линий действия. Второй - 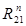 имеет начало в конце вектора
имеет начало в конце вектора 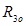 , а конец в полюсе.
, а конец в полюсе.
6.Построить полный вектор  как сумму нормальной и касательной его составляющих.
как сумму нормальной и касательной его составляющих.
7.Определить значения неизвестных векторов 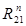 ,
,  и
и 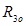 . Для этого необходимо их измерить и разделить на масштаб
. Для этого необходимо их измерить и разделить на масштаб  .
.
3.6. Выделить ползун 3 и показать все силы, действующие на него.
3.7. Графо-аналитическим методом решить второе уравнение системы (3.1), расписанное для ползуна:
 (3.8)
(3.8)
Где  - сила инерции третьего звена, Н;
- сила инерции третьего звена, Н;
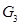 - сила тяжести третьего звена, Н;
- сила тяжести третьего звена, Н;
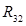 - сила взаимодействия третьего и второго звена, Н.
- сила взаимодействия третьего и второго звена, Н.
Для нахождения неизвестной силы 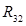 построить план сил по методике, описанной в пункте 3.5.
построить план сил по методике, описанной в пункте 3.5.
3.8. Выделить начальное звено и определить уравновешивающий момент или уравновешивающую силу. Для этого достаточно решить уравнение: сумма моментов относительно точки О равна 0.
 (3.9)
(3.9)
Распишем уравнение (3.9):
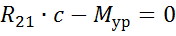 (3.10)
(3.10)
Где с – плечо от точки 0 до действия силы  , м;
, м;
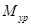 - уравновешивающий момент, Н∙м.
- уравновешивающий момент, Н∙м.
Уравновешивающую силу можно найти из соотношения
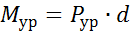 (3.11)
(3.11)
Где  - уравновешивающая сила, Н;
- уравновешивающая сила, Н;
d – плечо от точки 0 до действия силы  , м.
, м.
Направление уравновешивающей силы можно найти, решив графо-аналитическим способом второе уравнение системы (3.1), которое можно записать в следующем виде:
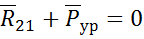 (3.12)
(3.12)
3.9. Варианты заданий для силового расчёта кривошипно-ползунного механизма Рис.3.1.1 сведены в табл.3.1.
Таблица 3.1
| Номер варианта |  ,
кг∙м ,
кг∙м
|  ,
м ,
м
|  ,
м ,
м
| 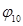 ,
град ,
град
|  ,
рад ∕с ,
рад ∕с
|  ,
кг ,
кг
| 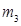 ,
кг ,
кг
| 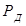 ,
Н ,
Н
|
| 0,1 | 2,0 | 5,0 | ||||||
| 0,1 | 1,4 | 3,5 | ||||||
| 0,1 | 1,1 | 2,6 | ||||||
| 0,1 | 1,2 | 3,0 | ||||||
| 0,1 | 0,8 | 3,5 | ||||||
| 0,1 | 1,0 | 3,0 | ||||||
| 0,1 | 2,0 | 4,2 | ||||||
| 0,1 | 0,5 | 4,5 | ||||||
| 0,1 | 0,8 | 2,0 | ||||||
| 0,1 | 1,4 | 3,5 | ||||||
| 0,1 | 1,2 | 3,0 | ||||||
| 0,1 | 1,4 | 3,2 | ||||||
| 0,1 | 1,1 | 4,1 | ||||||
| 0,1 | 0,8 | 2,5 | ||||||
| 0,1 | 0,6 | 2,0 | ||||||
| 0,1 | 0,5 | 1,5 | ||||||
| 0,1 | 0,2 | 3,0 | ||||||
| 0,1 | 1,0 | 2,1 | ||||||
| 0,1 | 1,4 | 3,5 | ||||||
| 0,1 | 2,0 | 5,5 |