ОБЩИЕ СВЕДЕНИЯ О СТРОЕНИИ МАТЕРИАЛОВ

В электронике используются материалы, находящиеся в различном агрегатном состоянии: газообразном, жид­ком, твердом и плазменном. Наибольшую группу состав­ляют твердые материалы, находящиеся в кристалличес­ком состоянии.

Кристаллы — твердые тела в виде выпуклых много­гранников с более или менее плоскими гранями и прямо­линейными ребрами. Материальные частицы расположе­ны в кристаллическом пространстве строго закономерно или периодически наподобие пространственной или крис­таллической решетки. Следовательно, для кристаллов ха­рактерно решеточное строение.

Благодаря периодичности внутренней структуры крис­таллы обладают симметрией, т.е. закономерной повторяе­мостью в пространстве равных фигур или равных частей одной и той же фигуры.

Основные свойства кристаллов:

• однородность;

• дискретность;

• анизотропия;

• способность самоограняться;

• полиморфизм.

Однородность — свойство вещества быть одинаковым во всем объеме. Это означает, что каждой точке кристал­ла в определенном направлении и на определенном рас­стоянии соответствует (находится) точно такая же и оди­наково расположенная точка. Однородность присуща не только кристаллическим телам.

Дискретность заключается в том, что в кристалле все­гда можно выделить микрообъем, в котором нет двух оди­наковых точек или материальных частиц.

Свойства однородности и дискретности кристаллов про­тиворечат друг другу. Однако для описания свойств крис­таллов достаточно рассматривать объемы большие, чем одна частица, но меньшие, чем целый кристалл. При та­ком подходе кристалл рассматривается как однородная, или сплошная, среда.

Анизотропия проявляется в том, что электрические, механические, тепловые, оптические и т.д. свойства крис­талла одинаковы по параллельным и связанным симмет­рией направлениям и, в общем случае, неодинаковы по непараллельным направлениям. Это связано с тем, что по разным направлениям различны расстояния между час­тицами и силы связи, следовательно, свойства будут раз­личными.

Анизотропной, в частности, является скорость роста кристалла. Если бы она была одинаковой по всем направ­лениям, то кристалл вырастал бы в форме шара. Именно благодаря анизотропии проявляется свойство кристалла самоограняться.

Способность самоограняться выражается в том, что в процессе роста кристалл приобретает вполне конкретную геометрическую форму с плоскими гранями и прямоли­нейными ребрами наподобие законченной геометрической фигуры в виде многогранника.

Полиморфизм — свойство веществ кристаллизоваться, в зависимости от условий, в двух и более кристаллических структурах. Каждая из структур формируется в опреде­ленном диапазоне температур и давлений. Такие структу­ры принято называть полиморфными формами, или поли­морфными модификациями. Модификации, устойчивые при нормальной (300 К) и более низкой температуре, обозна­чают буквой а, а устойчивые при более высоких темпера­турах — буквами β, γ, и т.д.

Примером наличия полиморфных модификаций крис­таллического состояния вещества является углерод. При обычных условиях углерод кристаллизуется в модифика­ции графита, а при повышенных температурах (порядка 2000 °С) и давлении (порядка 10¹⁰ Па) - в модификации алмаза.

В зависимости от условий роста форма и размеры гра­ней кристалла и полиморфных модификаций могут изме­няться. Однако углы между соответствующими гранями остаются постоянными. В этом заключается закон посто­янства углов для всех кристаллов, в том числе для каж­дой из модификаций веществ, обладающих полиморфиз­мом. Поэтому по значениям углов между гранями можно точно определить, из какого вещества сформирован крис­талл или в какой полиморфной модификации произошла кристаллизация.

Следует различать монокристаллические, поликристал­лические и аморфные структуры твердых тел.

Монокристаллическими являются достаточно большие по объему твердые тела со строго закономерным располо­жением материальных частиц во всем кристаллическом пространстве в виде законченного геометрического много­гранника.

Поликристаллической структурой обладают твердые тела, состоящие из очень большого числа мелких монокристалликов, хаотично ориентированных во всем объеме тела. Считается, что если нельзя определить характерную геометрическую форму монокристалликов, то состояние вещества принято называть квазиморфным.

Аморфными являются твердые тела, в которых отсут­ствует закономерное расположение материальных частиц в объеме. Поэтому аморфные вещества имеют одинаковые свойства по всем направлениям и являются изотропны­ми.

Кристаллическое состояние вещества наиболее устойчи­во. Это объясняется тем, что при закономерном располо­жении материальных частиц в кристаллическом простран­стве они занимают такое пространственное положение, при котором вся система частиц обладает минимальной внут­ренней энергией и, следовательно, наиболее устойчивым состоянием. За счет этого кристаллы имеют строго фикси­рованную температуру плавления Т_пл (рис. 1.6).

До момента времени t₁ температура кристаллического вещества растет пропорционально подводимой энергии и оно находится в твердом состоянии.

С момента t₁ - начала плавления- подводимая тепло­вая энергия тратится на разрушение кристаллического со­стояния, при этом температура расплавляемого кристал­лического вещества остается постоянной вплоть до пере­хода при t₂ в жидкое состояние всего объема вещества. При дальнейшем сообщении тепловой энергии температу­ра расплава начинает увеличиваться. Аморфные вещества переходят в вязкое, а затем в жидкое состояние при плав­ном повышении температуры, т.е. не имеют фиксирован­ной температуры плавления.

Жидкие кристаллы, используются в технике. Они обладают свойствами жидкости, такими, как текучесть, и могут находиться в каплевидном состоянии. Для них харак­терна анизотропия свойств, в том числе оптическая ани­зотропия. Материальные частицы в жидких кристаллах связаны слабыми межмолекулярными силами, поэтому структура кристаллов и их свойства сильно зависят от внеш­них факторов, таких, как электрическое поле, температу­ра, давление. Благодаря особым свойствам их применяют в качестве жидкокристаллических индикаторов в элект­ронных часах, дисплеях вычислительных машин, экранах телевизоров и т.д.

 

1.4.1. Строение кристаллов

Закономерное расположение материальных частиц (ато­мов, ионов, групп атомов, молекул) в кристаллическом пространстве экспериментально подтверждается с помощью рентгеноструктурного анализа. Было обнаружено (в 1912— 1913 гг.), что материальные частицы в кристаллах распо­ложены так же, как узлы пространственной решетки.

Пространственная решетка представляет собой пери­одическое расположение в пространстве математических точек. С помощью пространственной решетки можно мо­делировать структуру кристалла. Если в узлах простран­ственной решетки находятся атомы кристалла, то такую решетку принято называть кристаллической. Если совме­стить узел пространственной решетки с группой атомов, называемых базисом, то при повторении в пространстве базиса образуется кристаллическая структура (рис. 1.7).

Таким образом, кристаллическая структура представ­ляется (моделируется) как результат совмещения базиса с пространственной решеткой.

Идеальный кристалл можно представить закономерным повторением в пространстве одинаковых структурных еди­ниц, занимающих определенный объем и называемых эле­ментарной ячейкой (ЭЯ). Принято считать, что ЭЯ имеет форму параллелепипеда, или «кирпичика». Таким обра­зом, кристалл представляет собой пространство, заполнен­ное плотно прилегающими друг к другу элементарными ячейками.

С другой стороны, кристаллическое тело может быть смоделировано пространственной решеткой, состоящей из узлов, рядов и плоских сеток. Они соответствуют верши­нам, ребрам и граням элементарной ячейки кристалла (рис. 1.8).

Теорию решеточного строения кристаллов предложил в 1848 г. французский кристаллограф О.Браве. Русский кристаллограф Е.С. Федоров в 1890 г. на основе законов симметрии и математических преобразований доказал, что в кристаллах возможны 230 вариантов закономерного расположения частиц внутри кристаллического простран­ства. Их принято называть федоровскими группами сим­метрии.

 

1.4.2. Элементарные ячейки пространственных решеток

В общем случае ЭЯ трехмерных решеток в форме па­раллелепипеда характеризуется векторами элементарных трансляций (перемещений) а, b, с и углами между ними α, β, γ (Рис. 1.9).

Заполнение кристалли­ческого пространства осу­ществляется перемещени­ем ЭЯ, которое принято ха­рактеризовать вектором трансляции Т, равным

Т = п₁а + n₂b + п₃с,

где п₁ п₂, п₃ — целые, положительные и отрицательные числа, включая ноль.

 

При перемещении ЭЯ только вдоль одной оси коорди­нат, например вдоль Y, Т = п₂b, а п₁ =n₃=0. Отрицатель­ные значения п будут в случае перемещения ЭЯ в сторо­ны, противоположные направлениям осей координат. Тог­да вектор трансляции Т записывается в форме

Т = п₁а + п₂ b + п₃с.

Рассмотренная ЭЯ содержит в объеме один узел или атом, поэтому она называется простой, или примитивной, и обозначается Р.

Количество атомов в ЭЯ рассчитывается исходя из того, что каждый узел принадлежит одновременно восьми ЭЯ. Следовательно, узел принадлежит данной ЭЯ только 1/8 своей частью. В ЭЯ восемь вершин (узлов), поэтому число атомов будет равно N=1/8*8=1.

Элементарная ячейка, содержащая в объеме более од­ного атома или атомы разных химических элементов, на­зывается сложной.

Сложные типы ЭЯ представлены на рис. 1.10.

Когда в центре ЭЯ находится дополнительный атом ячейка называется объемоцентрированной, обозначается I и содержит в объеме количество атомов

N = (1/8 • 8) + 1 = 2.

Для кристаллов с кубической структурой ЭЯ имеет форму куба. Ее принято называть объемоцентрированная кубическая и обозначать ОЦК.

Если в центре двух противоположных граней ЭЯ нахо­дятся дополнительные атомы, то такая ячейка называется боконцентрированной, или базоцентрированной, и обозна­чается С. Каждый дополнительный атом на грани ЭЯ принадлежит ей только 1/2 своей частью. Поэтому коли­чество атомов в объеме такой ячейки

N = (1/8 • 8)+ (1/2 • 2) = 2.

Когда в центрах всех шести граней ЭЯ находятся ато­мы, ячейка называется гранецентрированной, обозначает­ся F и содержит количество атомов в объеме

N = (1/8 • 8)+ (1/2 * 6) = 4.

Для кристаллов кубической структуры ЭЯ принято на­зывать гранецентрированная кубическая и обозначать ГЦК.

В кристаллах существует особый тип примитивной ЭЯ, которая называется ромбоэдрической типа R (рис. 1.11). Она содержит в объеме один атом. Грани ячейки являют­ся ромбом.

Рассмотренные пять типов ЭЯ в различных структурах кристаллов отличаются соотношением длин векторов эле­ментарных трансляций а, b, с и углами между ними α,β,γ. Поэтому общее количество ЭЯ в кристаллах, выявленных О. Браве, четырнадцать. Их при­нято называть ячейками Браве, а про­странственные решетки, сформирован­ные повторением ЭЯ в кристалличес­ком пространстве, - решетками Бра­ве.

 

1.4.3. Кристаллические системы

По типу ЭЯ, как простых, так и сложных, и по свой­ствам симметрии реальные кристаллы в зависимости от структуры подразделяются на семь кристаллических сис­тем (табл. 1.1).

1.4.4. Кристаллографическая индексация

Для определения положения узлов, рядов, направлений и плоскостей в кристаллическом пространстве существу­ет система обозначений, т.е. система индексации перечис­ленных характеристик кристаллов. Особенность системы индексации состоит в том, что координаты узлов и длины отрезков, отсекаемых плоскостями по осям координат или ребрам кристаллов, измеряются количеством векторов элементарных трансляций.

Положение узла пространственной решетки определя­ется его координатами по соответствующим осям, т.е.

х = п₁а; у = n₂b; z = п₃с,

где n_v n₂, п₃ — целые положительные и отрицательные числа, соответствующие числу векторов элементарных трансляций по осям координат.

За начало координат принимается любой узел простран­ственной решетки (рис. 1.12).

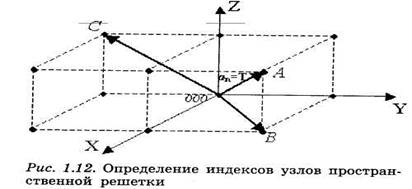
Положение узла определяется радиус-вектором а_п или равным ему вектором трансляции Т, т.е.

а_п= Т = n₁a. + n₂b + п₃с

Численные значения п₁, п₂, п₃ называются индексами узла, а их значения, записанные в двойные скобки, — сим­волом узла. Для узлов А, В и С, приведенных на рисунке, символы записываются [[111]], [[110]], [[01l]] соответствен­но.

Положение ряда точек или узлов в кристаллическом пространстве определяется двумя точками. Одна из точек может быть выбрана за начало координат. Тогда коорди­наты второй точки (узла), выраженные в количестве век­торов элементарной трансляции, будут индексами ряда. Координаты узлов ряда или направления принято обозна­чать х = иа, у = vb, z=wc, где и, v, w- целые положитель­ные и отрицательные числа, включая ноль. Численные значения и, v, w называются индексами ряда, а заключив их в квадратные скобки [и v w], получают символ ряда.

Таким образом, кристаллографическое направление (уз­ловой ряд решетки) определяется координатами узла, бли­жайшего к началу координат (рис. 1.13).

Отличие в обо­значении символов узлов от рядов и направлений заклю­чается в использовании двойных или одинарных квадрат­ных скобок.

Следует подчеркнуть, что параллельные ряды тожде­ственны, поэтому они имеют одинаковый символ. Любой ряд можно переместить параллельно самому себе так, что­бы он прошел через начало координат и ближайший узел решетки, координаты которого являются символом ряда (направления).

Индексы и символ плоскости определяются длинами отрезков, отсекаемых плоскостью по осям координат. В общем случае узловая плоскость в кристалле отсекает раз­личные по длине отрезки та, nb, рс, на которых уклады­вается целое число векторов элементарных трансляций (рис1.14)

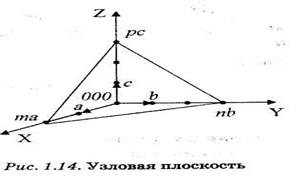
Величины, обратные дли­нам отрезков, отсекаемых плоскостью по осям коорди­нат, называются индексами Миллера и обозначаются hkl. Заключив индексы в круглые скобки, получают символ плоскости (hkl).

Таким образом, индексы hkl — это три целых поло­жительных или отрицатель­ных числа, включая ноль, ко­торые получают из соотно­шения:

Для получения целочисленных значений hkl отноше­ние обратных величин длин отрезков приводится к обще­му знаменателю, который отбрасывается, а числители бу­дут индексами Миллера.

Чем больший отрезок отсекает плоскость на коорди­натной оси, тем меньше численное значение индекса в сим­воле плоскости, относящегося к данной оси. Для рис. 1.14 и расчета самый большой отрезок отсекает плоскость по оси Z, а соответствующий индекс 3 в символе плоскости самый меньший.

Если плоскость параллельна одной из осей координат (рис. 1.15, а), то она отсекает на ней бесконечно большой отрезок. Следовательно, индекс в символе плоскости, соот­ветствующий этой оси, будет 0. Если плоскость парал­лельна двум осям координат (рис. 1.15, б), то в символе плоскости два индекса будут равны нулю. Если плоскость отсекает отрезок на отрицательном направлении оси ко­ординат (рис. 1.15, в), то над индексом для этой оси ставится знак минус.

Все параллельные плоскости имеют один и тот же об­щий символ с малыми численными значениями индексов. Любую плоскость можно переместить параллельно самой себе вплоть до плоскости, ближайшей к началу координат, которая имеет наименьшие численные значения индексов. Для обозначения системы параллельных плоскостей в кри­сталле символы hkl записываются в фигурные скобки, т.е. { hkl }.

Плоскость, отсекающая по осям координат отрезки, рав­ные единичным векторам трансляции, называется единич­ной плоскостью. Если плоскость не проходит через узлы решетки, следовательно, она отсекает по осям координат отрезки, равные дробным величинам векторов элементар­ных трансляций (рис. 1.16). Целочисленные значения ин­дексов такой плоскости определяются по приведенной выше методике,

В кристалле важными явля­ются направления, перпендику­лярные узловым плоскостям. Проекция плоскости на это на­правление позволяет опреде­лить плотность упаковки ато­мов по данному направлению, а следовательно, выявить на­личие анизотропии свойств по различным направлениям в кристалле (рис. 1.17).

 

 

1.4.5. Дефекты структуры кристаллов

Дефект — любое отклонение от периодичности струк­туры кристалла. В зависимости от мерности дефекта вы­деляют дефекты:

• нульмерные, или точечные;

• одномерные, или линейные;

• дзухмерные, или плоские;

• трехмерные, или объемные.

Дефекты существенно влияют на многие свойства крис­таллов. При отсутствии дефектов была бы невозможна пластическая деформация металлов и управление типом проводимости в полупроводниках. Поэтому в полупровод­никах дефекты создают искусственным путем — терми­ческой диффузией или ионной имплантацией атомов при­меси в приповерхностный слой монокристалла.

Любой тип дефектов кристалла изменяет энергетичес­кий спектр электронов, а следовательно, и свойства мате­риала, зависящие от него.

Точечными дефектами являются:

— вакансии, т.е. смещение собственного атома в меж­доузлие;

— примеси чужеродных атомов, которые могут нахо­диться либо в позиции замещения собственного атома в узле решетки, либо в позиции внедрения в междоузельное пространство решетки.

По механизму образования точечных дефектов в крис­талле различают дефекты по Шоттки и дефекты по Френ­келю.

Механизм образования дефектов по Шоттки заключа­ется в перемещении атома из узла решетки на поверхность, где он начинает формирование нового атомного ряда. На его месте образуется вакансия, которая за счет эстафетно­го заполнения соседними атомами перемещается вглубь кристалла (рис. 1.18). При этом изменяется плотность кристалла за счет увеличения объема при сохранении ко­личества атомов в кристалле.

Механизм образования дефектов по Френкелю заклю­чается в перемещении атома из узла решетки в междоуз­лие. В результате образуется пара точечных дефектов: атом в междоузлии и вакансия. Она перемещается вглубь крис­талла и может находиться далеко от междоузельного ато­ма Конструкция дефектов по Шоттки и Френ­келю при термодинамическом равновесии определяется природой и структурой кристалла.

Точечные дефекты по Шоттки и Френкелю, как и ато­мы примеси в позиции внедрения или замещения, приво­дят к локальному искажению структуры, вызывая внут­ренние механические напряжения в виде сжатия и растя­жения решетки. При наличии вакансии (рис. 1.20, а) ато­мы первой координационной сферы сдвигаются к вакан­сии, т.е. подвержены сжатию. Атомы второй координаци­онной сферы отталкиваются от вакансии, т.е. решетка под­вержена растяжению. Собственные и примесные атомы в междоузлиях и атомы примеси в позиции замещения (рис. 1.20, б) приводят к локальному растяжению решетки.

Линейные дефекты структуры кристаллов называются дислокациями. Они возникают в результате скольжения части кристалла вдоль атомных плоскостей на одну транс­ляцию. Вследствие этого нарушается чередование атомных плоскостей в отдельной части кристалла. Дислокации по­являются при термической, механической обработке и в процессе выращивания монокристаллов.

 

Принято различать краевую, винтовую и криволиней­ную дислокации.

Краевая дислокация возникает при скольжении вдоль атомных плоскостей, в результате чего появляется лиш­няя полуплоскость, край которой внутри кристалла обра­зует линейный дефект, являющийся краевой дислокаци­ей (рис. 1.21).

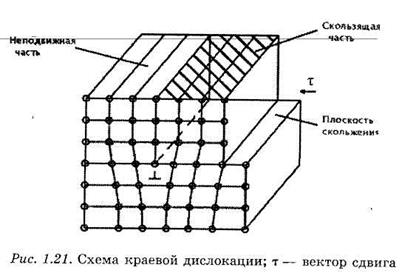
Вблизи краевой дислокации решетка деформирована, причем есть области растяжения и сжатия.

В кристалле возможны краевые дислокации разного знака (рис. 1.22). При деформации разнополюсные дисло­кации могут двигаться навстречу друг другу и слиться в одну плоскость. Это явление называется аннигиляцией дис­локаций. Решетка при этом восстанавливается.

Винтовая дислокация возникает при напряжении сдви­га в части кристалла, перпендикулярном атомным плос­костям (рис. 1.23).

В результате на торцевой поверхности происходит сме­щение плоскостей на одно межплоскостное расстояние (на вектор элементарной трансляции). Деформированная часть кристалла отделяется от недеформированной относитель­но оси дислокации С по спиральной (винтовой) кривой, обозначенной пунктиром. Это и послужило появлению тер­мина «винтовая дислокация».

 

Криволинейная дислокация является общим случаем наличия в кристалле краевой и винтовой дислокаций. В отличие от прямолинейных осей краевой и винтовой дис­локаций ось криволинейной дислокации образует в крис­талле пространственную кривую линию. Она либо замыкается в петлю внутри кристалла, либо выходит на его поверхность.

Для количественной оценки степени нарушения струк­туры за счет линейных дефектов принято определять плот­ность дислокации, т.е. количество дислокаций, выходящих на единице поверхности кристалла. Для хорошо сформи­рованных монокристаллов Ge и Si плотность дислокаций составляет (10²...10³) см^-2, для сильно деформированных металлов она достигает значений (1О¹¹...1О¹²) см^-2.

С дислокациями принято связывать границы зерен по­ликристаллических веществ. Считается, что параллельные краевые дислокации концентрируются вдоль границ поли­кристаллов, когда углы между кристаллическими плоско­стями соприкасающихся поликристаллов невелики. В этих случаях говорят о дислокациях малоугловых границ или об образовании дислокационных стенок.

Двухмерными дефектами называют скопления вакан­сий, внедрений и атомов замещения в части кристалло­графической плоскости (рис. 1.24). Скопления точечных дефектов называются кластерами.

Постоянно присутствующим двухмерным дефектом является поверхность, ограничивающая кристалл. Поверх­ностные атомы не окружены со всех сторон другими ато­мами, как в объеме кристалла. Поэтому их пространствен­ное положение отличается от положения атомов в объеме. Искажения кристаллической решетки наблюдаются в при­поверхностном слое глубиной от десятков межатомных расстояний и выше. В результате свойства приповерхност­ной области кристалла существенно отличаются от свойств объема.

Трехмерными дефектами являются пустоты, трещи­ны, поры, включения разного рода примесей. Любые дефекты структуры существенно влияют на механические, тепловые, электрофизические, оптические и магнитные свойства твердых тел.

 

Тема № 3.

Типовые материалы, применяемые в качестве проводников