Наиболее общая структура системы ЧПУ показана на рис. 1.4. Ниже рассмотрены основные функции элементов этой системы.
Управляющая программа задаёт последовательность требуемых по технологии действий электроприводов и вспомогательных механизмов. Например, перемещение инструмента по линейной траектории, смена инструмента и др. Задачей интерпретатора является анализ кода управляющей программы и формирование на его основе признаков траектории движения: типа траектории (линейная, круговая, винтовая), координат конечной точки траектории и центра окружности (при отработке круговой траектории), линейной скорости движения инструмента. Далее эти данные подвергаются эквидистантной коррекции и передаются следующему звену системы – интерполятору. Интерполятор определяет необходимое положение приводов в каждый момент времени, т. е. рассчитывает координаты всех точек траектории от начала до конца отрабатываемого участка с учётом ограничений на ускорение приводов. Таким образом, интерполятор формирует сигналы задания на регуляторы положения всех осей системы.
Электроавтоматика и пр.
Рис. 1.4. Структурная схема системы числового программного управления
АЛГОРИТМЫРЕШЕНИЯ ОСНОВНЫХ ЗАДАЧ ЧПУ
Интерполяция
Одной из основных задач, решаемых любой системой ЧПУ, является обеспечение движения инструмента относительно детали по заданной траектории. Траектория движения аппроксимируется набором кривых. Для подавляющего большинства современных систем ЧПУ допустимыми кривыми являются отрезки прямых и дуги окружностей. Каждый участок траектории задается координатами начальной и конечной точек и параметрами уравнения участка. Для управления движением инструмента по заданной траектории необходимо знать текущие значения всех координат и на основании этих значений формировать управляющие воздействия на приводы. Расчёт текущих значений координат называется интерполяцией.
При линейной интерполяции (для линейного участка) в кадре указываются тип интерполяции (G01) и координаты конечной точки участка.
При круговой интерполяции (для участка в виде дуги окружности) в кадре указываются тип интерполяции c направлением движения (G02 – круговая интерполяция по часовой стрелке, G03 – против часовой стрелки) и параметры интерполяции в виде координат конечной точки участка и координат центра дуги. Координаты начальной точки во всех случаях являются координатами конечной точки предыдущего участка.
Алгоритмы интерполяции можно разделить на две группы. К первой относятся алгоритмы, задачей которых является определение момента выдачи единичных приращений по координатам (квантов перемещения). Частота выдачи приращений зависит от скорости изменения координаты. Алгоритмы второй группы отличаются постоянством периода расчёта текущих значений координат. Задача алгоритмов состоит в определении приращения координаты, накопленного за этот период (квант времени). Квант времени неизменен, приращения зависят от скорости изменения координат.
К первой группе относятся алгоритм оценочной функции и метод цифрового дифференциального анализатора, ко второй группе – метод цифрового интегрирования. В многоцелевых системах ЧПУ широко применяют алгоритмы интерполяции, относящиеся ко второй группе, поэтому они будут рассмотрены наиболее подробно. Из алгоритмов первой группы остановимся на методе оценочной функции, который применяют при управлении технологическим оборудованием с шаговыми двигателями.
Интерполяция обычно ведётся в абстрактных (обобщённых) координатах α, β, γи т. д. (в отличие от реальных, приведенных к объекту координат х, у, z,...). Переименование координат проводится при интерпретации кадра таким образом, чтобы интерполируемый отрезок находился в первом квадранте (например, в качестве α принимается значение y, в качестве β – z и т. д.). Обратное переименование выполняется перед выдачей сигналов на привод. Переход к абстрактным координатам объясняется стремлением уменьшить разнообразие алгоритмов интерполяции. Например, ход алгоритма зависит от того, по какой из координат задано наибольшее приращение (так называемая ведущая координата). Максимальной может быть любая из координат х, у, z,..., но при переходе к абстрактным координатам её всегда обозначают через α.
2.1.1. Интерполяция по методу оценочной функции. По алгоритму оценочной функции с определенной частотой, зависящей от скорости перемещения, анализируется знак так называемой оценочной функции, и в зависимости от него выдается сигнал изменения на один квант расчетного значения одной или другой координаты. Масштаб приращений выбирается так, чтобы квант соответствовал единице младшего разряда слова системы ЧПУ.
2.1.1.1. Линейная интерполяция по методу оценочной функции. На рис. 2.1 показано движение по методу оценочной функции вдоль прямой, т. е. при линейной интерполяции. Начало воспроизводимого участка условно совмещается с началом координат. Для этого достаточно в качестве координат αк, βк конечной точки задавать приращения Δα и Δβ. На рисунке показано положение прямой в первом квадранте (Δα и Δβ – положительные). Для воспроизведения прямых в других квадрантах справедлив тот же алгоритм, но выходным сигналам на привод присваивается соответствующий знак приращения.
Плоскость координат делится на две полуплоскости: над прямой и под прямой. Оценочная функция F (α, β) вводится таким образом, чтобы в верхней полуплоскости выполнялось условие F (α, β) > 0, в нижней – F (α, β) < 0, на прямой – F (α, β ) = 0. Управление движением происходит по следующим правилам. Если в данный момент (при данном состоянии текущих координат) значение оценочной функции положительно: F (α, β) > 0, то делается шаг по координате α, если отрицательно: F (α, β) < 0 – шаг по координате β. При F (α, β) = 0 выполняется шаг по ведущей координате, имеющей наибольшее приращение в кадре.
Рис. 2.1. Линейная интерполяция по методу оценочной функции
В качестве оценочной функции в любой точке можно принять разность текущего β и расчётного βр значений координаты при заданном значении α, то есть, F (α, β) = β – βр. Из уравнения прямой получаем расчётное значение координаты βр = (βк/αк) . α. Следовательно, F (α, β) = β – (βк/αк), а поскольку имеет значение только знак этой функции, характеризующий отклонение точки от заданной прямой, можно предложить эквивалентное выражение для оценочной функции:
F (α, β) = αкβ – βкα.(2.1)
Составим рекуррентные выражения для вычисления очередного значения оценочной функции через её предыдущее значение. Если выполняется шаг по координате β, то оценочная функция изменяется следующим образом:
F (α i, β i +1) = (β i +1)αк – α i βк = β i αк – α i βк + αк.
Используя уравнение (2.1), получим
F (α i, β i +1) = F (α i, β i) + αк.(2.2)
Аналогично, выполняя шаг по координате α, получим закон изменения оценочной функции:
F (α i +1, β i) = F (α i, β i) – βк.(2.3)
Алгоритм, реализующий формулы (2.2) и (2.3), может быть усовершенствован за счёт выдачи приращений по максимальной координате на каждом кванте времени. Если обозначенную через α максимальную координату откладывать по оси абсцисс, то при положительном значении оценочной функции необходимо выдавать приращения только по α, а при отрицательном и равном нулю значениях – одновременно по обеим координатам α и β. В этом случае новое значение оценочной функции рассчитывается по формуле
F (α i +1, β i +1) = F (α i, β i) + αк – βк.
Достоинство этого алгоритма заключается в том, что при движении вдоль прямой под углом 45° к координатным осям максимальная скорость возрастает в два раза за счёт одновременного движения по координатам α и β.
Алгоритм оценочной функции легко распространяется на число координат больше двух. На рис. 2.2 в качестве примера приведен алгоритм для четырёх координат. Вводятся оценочные функции, связывающие каждую координату с максимальной координатой α. При постоянной выдаче приращений по максимальной координате контроль окончания отработки кадра можно также вести только по максимальной координате. Другим достоинством алгоритма, приведенного на рис. 2.2, является то, что, начиная работу по-разному, можно увеличивать максимальную скорость при уменьшении числа одновременно работающих координат. Зная время реализации алгоритма Тn,здесь n – число одновременно работающих координат, можно определить максимальную скорость подачи вдоль одной координатной оси: V п max = (h / Tn)где h – значение единичного шага перемещения (дискретность). Максимальная контурная скорость V к max зависит от соотношения приращений по координатам и становится наибольшей, когда приращения равны, при этом 
.
Поскольку максимальная скорость подачи систем ЧПУ, работающих по методу оценочной функции, зависит от дискретности выдаваемой информации, то для таких систем обычно указывают оценку быстродействия в виде f max= 1/ Tn, т. е. в виде максимальной частоты выходных импульсов на привод по одной координате. Необходимая в данный момент частота f выдачи шагов определяется заданной скоростью V п подачи и углами наклона траектории к осям координат:
. (2.4)
Рис. 2.2. Алгоритм линейной интерполяции по методу оценочной функции
Подготовка исходных данных для одного кадра линейной интерполяции по методу оценочной функции сводится к следующим этапам:
– реальные координаты х, у, z,... и направления движения по ним ставятся в соответствие обобщенным координатам α, β, у,..., причём в качестве α принимается максимальная координата;
– по формуле (2.4) рассчитывается частота шагов интерполяции;
– выбирается начало алгоритма (см. рис. 2.2) в зависимости от числа ненулевых координат.
2.1.1.2. Круговая интерполяция по методу оценочной функции. При круговой интерполяции, т. е. движении по отрезку дуги, за начало координат при отработке кадра принимается центр окружности (рис. 2.3). Интерполяционные расчёты ведутся для дуги, расположенной в первом квадранте абстрактной системы координат при движении по часовой стрелке.
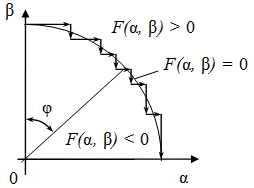
Рис. 2.3. Круговая интерполяция по методу оценочной функции
Если дуга расположена в других квадрантах или движение происходит против часовой стрелки, то это учитывается при переходе от реальных координат к абстрактным и выборе знаков перемещений в соответствии с табл. 2.1. Таблица составлена для плоскости X-Y, аналогичные таблицы создаются и для плоскостей Y-Z и Z-X.
Таблица 2.1
Правила перехода от реальных координат к обобщённым
| Номер квадранта | При движении | |||
| по часовой стрелке | против часовой стрелки | |||
| x | y | x | y | |
| α | β | β | α | |
| –α | β | –β | α | |
| –β | –α | –α | –β | |
| β | –α | α | –β |
Оценочная функция F (α, β) выбирается таким образом, чтобы при нахождении точки внутри круга выполнялось условие F (α, β) < 0, вне круга – F (α, β) > 0, на окружности – F (α, β) = 0. В качестве оценочной функции удобно принять разность текущего и расчётного значений радиуса или, поскольку для выбора направления очередного шага имеет значение только знак функции, разность квадратов радиусов. Используя уравнение окружности, получаем: F (α, β) = α2 + β2 – R2. Если F (α, β) < 0, то выполняется шаг в сторону увеличения α. При этом новое значение оценочной функции определяется из выражения
. (2.5)
При F (α, β) > 0 выполняется шаг в сторону уменьшения β. Новое значение оценочной функции будет иметь вид
. (2.6)
Для повышения контурной скорости можно усовершенствовать алгоритм, реализующий формулы (2.5) и (2.6), за счёт выдачи на каждом шаге приращений по ведущей координате, т.е. имеющей наибольшее приращение в кадре. На участке изменения угла φ от 0 до 45° (см. рис. 2.3) такой координатой является α, на участке 45° < φ < 90° – координата β. Для выявления ведущей координаты можно использовать разность текущих значений (α – β). При одновременной выдаче шагов по обеим координатам с учетом (2.5) и (2.6) оценочная функция вычисляется следующим образом:
.
Алгоритм движения по дуге окружности с одновременной выдачей шагов по двум координатам приведен на рис. 2.4. Поскольку исходная и конечная точки траектории (участка) могут лежать не точно на окружности, необходимо проверять окончание отработки кадра по обеим координатам. Для этого при достижении заданного значения одной из координат происходит переключение алгоритма на линейную интерполяцию по оставшейся координате (см. рис. 2.4).
При постоянстве частоты шагов контурная скорость будет иметь максимум в точке, лежащей на биссектрисе координатного угла. График изменения скорости при движении с постоянной частотой выдачи шагов представлен на рис. 2.5.
Рис. 2.4. Алгоритм круговой интерполяции по методу оценочной функции
Такое непостоянство скорости недопустимо с технологической точки зрения, поэтому необходимо корректировать частоту шагов. Можно показать, что на первом участке она должна уменьшаться с каждой выдачей шага по координате β на значение V к / R, а на втором участке – увеличиваться также при каждой выдаче шага по координате α(здесь V к – заданная контурная скорость).
Рис. 2.5. График изменения контурной скорости при круговой интерполяции
с постоянной частотой выдачи шагов
В общем случае для произвольной начальной точки внутри квадранта с координатами I и J начальная частота f н рассчитывается по формуле, аналогичной формуле (2.4),
. (2.7)
При подготовке исходных данных (интерпретации кадра) для круговой интерполяции по методу оценочной функции рассчитывается частота выдачи шага по формуле (2.7) и ставятся в соответствие обобщённые (абстрактные) и реальные координаты по табл. 2.1. Если заданная дуга расположена в нескольких квадрантах, то при подготовке управляющей программы в некоторых система ЧПУ её разбивают на несколько кадров.
Объединение алгоритмов линейной и круговой интерполяции (см. рис. 2.2 и 2.4) позволяет реализовать винтовую интерполяцию. Однако в этом случае дуга не должна выходить из половины квадранта, так как в одном кадре не должна изменяться ведущая координата. Обозначим через α и β координаты, осуществляющие движение по окружности, а через γ – третью координату. Если максимальное приращение в кадре (на участке) имеет одна из координат, например α, то сначала надо проанализировать оценочную функцию F (α, γ), определяемую по формулам линейной интерполяции (2.2) и (2.3). В зависимости от её знака выдается (или не выдается) шаг по γ,и далее реализуется алгоритм круговой интерполяции (см. рис. 2.4). Если максимальное приращение в кадре имеет координата γ, то постоянно выдаются шаги по γи на основании анализа той же оценочной функции в зависимости от её знака формируется переход на круговую интерполяцию. Максимальная контурная скорость, которую можно обеспечить при круговой или винтовой интерполяции, определяют по формуле h/T, где Т – время реализации соответствующего алгоритма в используемой ЭВМ.
Как при линейной, так и при круговой или винтовой интерполяции для организации разгона в начале участка и при необходимости торможения в конце участка должна изменяться частота выдачи шагов f. Значение Δ f, на которое необходимо изменить частоту выдачи на каждом шаге, определяется динамическими свойствами приводов станка, в частности, максимально допустимым ускорением a доп. Приближенно фактическое ускорение можно рассчитать по формуле a = f . Δ f .h. По этой формуле определяют допустимое изменение частоты для заданного значения a доп. Проверить.
Погрешность интерполяции по методу оценочной функции с учётом конечной разрядной сетки ЭВМ не превышает значения h. Достоинства метода оценочной функции заключаются в простоте стыковки с шаговыми двигателями, относительной простоте подготовки исходных данных для интерполяции, отсутствии накопления ошибки при расчете траектории и требовании небольшой разрядности ЭВМ УЧПУ, определяемой максимальными значениями координат при принятой дискретности.
К недостаткам метода следует отнести сравнительно небольшую достижимую скорость перемещения, определяемую ценой шага и быстродействием УЧПУ, а также необходимость использования для связи с циклическими датчиками (вращающийся трансформатор, индуктосин) специального преобразователя из унитарного кода. Реализация преобразователя программным путём (подсчётом единичных приращений для каждой координаты) ведёт к дополнительным потерям вычислительных ресурсов, а следовательно, к снижению максимальной скорости подачи. Помимо этого, во многих системах ЧПУ для уменьшения динамической ошибки в состав управляющего сигнала вводят составляющую, пропорциональную скорости изменения координаты. При использовании метода оценочной функции величиной, пропорциональной скорости координаты, является частота выдачи приращений (шагов) по данной координате. Изменение частоты шагов пропорционально контурной скорости может быть выполнено либо аппаратурным, либо программным способом.
Разработчики современных систем ЧПУ довольно редко используют метод оценочной функции из-за малого значения максимальной контурной скорости и необходимости решения ряда задач с помощью специального оборудования. Однако полностью отказываться от этого метода считается преждевременным.
2.1.2. Интерполяция по методу цифрового интегрирования. В методе цифрового интегрирования (МЦИ) в основу вычислений положен квант времени (постоянная частота вычислений), а скорость по координате меняется за счёт выдачи различных (не только единичных) приращений по координатам. Таким образом, приращения накапливаются за равные промежутки времени.
По методу МЦИ значение i -й координаты и её скоростей в любой момент времени t могут быть вычислены по следующим формулам:
(3.8)
где Si 0, Vi 0 — начальные значения i -й координаты и её скорости соответственно (в момент времени t = 0); Si, Vi – текущие значения i- йкоординаты и её скорости в момент времени t соответственно; аi – текущее значение ускорения i -й координаты в момент времени t. В зависимости от заданного закона изменения ускорения аi от времени и от значения других координат получается движение по различным кривым. Вид интерполируемой кривой определяет метод цифрового интегрирования, наиболее пригодный для вычисления определенных интегралов (3.8), так как от вида кривой и метода вычисления зависит накопленная ошибка и время реализации алгоритма.
При линейной интерполяций требуется, чтобы скорости и ускорения по каждой координате в любой момент времени были пропорциональны приращениям этих координат на заданном участке. Для вычисления интегралов поформуле (3.8) можно применить наименее трудоемкий метод Эйлера(прямоугольников), так как погрешность метода не приводит к нарушению пропорциональности и не оказывает влияния на траекторию движения инструмента. При движении с постоянным ускорением скорость и координата на (j + 1)-м шаге могут быть вычислены через значения скорости и координаты на j -м шаге по следующим формулам:
(3.9)
где Δt – квант интегрирования по времени.
Так как этот квант постоянен, то в выражении (3.9) можно исключить операцию умножения, вводя соответствующим образом масштабы скорости и ускорения по координатам. За машинную единицу скорости целесообразно взять скорость в одну машинную единицу приращения координаты за время Δt. За машинную единицу ускорения принимается ускорение в одну машинную единицу приращения скорости за время Δt. В общем случае при отработке кадра с линейной интерполяцией можно выделить три участка: 1 – разгон, 2 – движение с постоянной скоростью и3 – торможение (рис. 3.6). На участке 1контурная скорость линейно увеличивается от начальной скорости V 0 до заданного значения V З. На участке 2контурная скорость остается постоянной и на участке 3контурная скорость линейно убывает от заданного значения V З до скорости в конце кадра V К.К. Моменты окончания разгона t Р, начала торможения t Т, окончания отработки кадра t К.К одинаковы для всех координат. Для кадров с малыми приращениями по координатам моменты t Р и t Т могут совпадать. Для определения этих моментов времени целесообразно ввести дополнительную ведущую координату S В. В качестветакой координаты можно взять либо координату, имеющую в данном кадре максимальное приращение, либо контурный путь, определяемый по формуле
(3.10)
где n – количество координат на станке.
Алгоритм линейной интерполяции представлен на рис. 3.7. Для снижения погрешности, накопленной при определении скорости на участке разгона за счёт неточности вычисления ускорения, в конце разгона скоростям присваиваются рассчитанные с точностью до половины младшего разряда заданные значения скоростей Vi З по каждой координате. Накопление ошибок значений координат от кадра к кадру исключается присвоением координатам в конце отработки кадра их точных для конца кадра значений Si К.К. Это приводит к тому, что за последний квант времени Δt работы по координате приращение может колебаться от единицы младшего разряда до величины Vi К.К Δt. В тех кадрах, где отсутствует торможение и движение происходит с большой скоростью, возможен кратковременный большой перепад реальной скорости задающего воздействия.
Рис. 3.6. График изменения контурной скорости в кадре
Этого можно было бы избежать, если выбрать скорость как частное от деления приращения по координате на целое число. Однако такой путь практически неосуществим из-за ошибок округления, возникающих при делении, и из-за наличия участков разгона и торможения. Поэтому в большинстве систем ЧПУ, использующих метод МЦИ, применяется другой способ. Оставшийся путь сравнивают с отрезком, равным V К.К N и как только он станет равным или меньше этого отрезка, рассчитывают новую скорость, равную оставшемуся пути, деленному на N. Таким образом, действительная скорость в конце кадра будет удовлетворять следующему неравенству:
V К.К (N– 1)/ N < V К.К.Д < V К.К,
где V К.К — заданная скорость в конце кадра; V К.К.Д – действительная скорость в конце кадра; N – целое число, выбираемое из минимально допустимого перепада скорости в конце кадра по всем координатам. Целесообразно выбрать N = 2 k. Тогда действительные значения скоростей в конце кадра могут быть получены сдвигом на k разрядов значений оставшихся отрезков по каждой координате. Для большинства современных станков k = 4 ÷ 5.
Рис. 3.7. Алгоритм реализации линейной интерполяции методом цифрового интегрирования на участке Δt
Рассмотрим инструментальную ошибку, возникающую при вычислении значений координат методом цифрового интегрирования из-за приближенного вычисления значений ускорений и скоростей по каждой координате. Без ущерба для общности приведенных ниже результатов можно допустить, что округление вычисленных значений происходит путём отбрасывания всех младших (незначащих) разрядов. Тогда при движении по двум координатам наибольшее отклонение от заданной траектории будет в конце кадра, если значение ускорения и скорости одной координаты вычислены точно, а другой – с максимальной погрешностью, равной единице младшего разряда.
Погрешность, накопленная по второй координате к концу кадра, будет иметь три составляющих: погрешности, накопленные на участках разгона и торможения за счёт неточности значения ускорения, и погрешность, накопленная при движении с постоянной скоростью за счёт неточности значения скорости. Обозначим N Р, N П, N Ткак числа тактов интегрирования на участках разгона, движения с постоянной скоростью и торможения соответственно, m – количество двоичных разрядов разрядной сетки ЭВМ. Тогда максимальная погрешность к концу кадра, выраженная в единицах младшего разряда, может быть определена из выражений
(3.11)
где Vmax – максимальная скорость; а доп – допустимое ускорение (значение N П определяется максимальным временем отработки кадра).
Формулы (3.11) позволяют оценить максимальную погрешность при линейной интерполяции, если известна разрядность управляющей ЭВМ, или по допустимой погрешности определить необходимую разрядность. Из формулы также видно, что применение высококачественных приводов (допускающих большие ускорения) существенно снижает инструментальную ошибку интегрирования.
Можно указать ещё один эффективный путь уменьшения инструментальной погрешности. Он заключается в расчёте промежуточных точек как на участке разгона, так и на участке движения с постоянной скоростью. При достижении этих точек значениям скоростей и координат присваиваются рассчитанные значения и таким образом уничтожается накопленная ошибка интегрирования.
Подготовка исходных данных для линейной интерполяции заключается в разложении по координатным осям следующих векторов: V0 – начальной контурной скорости; VЗ – заданной контурной скорости; а доп – допустимого ускорения.
Разложение выполняется по формулам:
; 
; 
,
где Vi0, ViЗ – начальная и заданная скорости i -й координаты; ΔSi — приращение в кадре по i -й координате; n — число координат; аi — ускорение по i -й координате.
Необходимо также определить путь торможения по ведущей координате ΔS Вторм по формуле
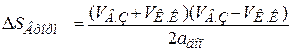. (3.12)
Если путь торможения окажется больше половины контурного пути, то он приравнивается к половине пути. Значение начальной скорости при этом должно быть не больше значения конечной скорости.
Круговая интерполяция может быть получена за счёт цифрового интегрирования дифференциальных уравнений окружности. Однако анализ погрешности показывает, что для получения требуемой точности необходимо применять методы интегрирования (Адамса, Рунге-Кутта), требующие значительного вычислительного времени. Рассмотрим алгоритм, основанный на вращении вектора с радиусом R и последующем его разложении по координатным осям в определенных дискретных точках. Момент окончания разгона определяют по достижению угловой скорости ω заданного значения. Момент начала торможения и окончания отработки кадра определяют по достижению углом φ соответствующих значений φ торм и φ к.к.
На первом этапе алгоритма рассчитывают новые значения угловой скорости ωi +1 и угла поворота φi +1, которые используют для определения моментов окончания разгона начала торможения и окончания отработки кадра:
; 
,
где ε — угловое ускорение.
На втором этапе определяют новые значения координат αi +1 и βi +1 (рис. 3.8):
; 
.
Учитывая, что φi +1 = φi + Δφi, где Δφi = (ωi + ωi+1) Δt /2, получаем
(3.13)
Ввиду малости значения Δφi можно принять cos Δφi ≈ 1 – 0,5 Δφi2; sin Δφi ≈ Δφi. Поскольку R cos φi = αi; R sin φi = βi, окончательно получим:
(3.14)
Рис. 3.8. Определение текущих значений координат при круговой интерполяции методом цифрового интегрирования
Для управления приводом обычно требуется формировать сигналы, пропорциональные скоростям по координатам. В качестве таких сигналов можно использовать приращения по координатам за отрезок времени Δt:
Алгоритм круговой интерполяции представлен на рис. 3.9. Расчёт текущих координат по формулам (3.11) содержит четыре операции умножения. Известно, что время выполнения умножения существенно зависит от количества разрядов множителя. Особенность рассмотренного алгоритма круговой интерполяции заключается в том, что точность интерполяции не зависит от количества разрядов Δφ. От количества разрядов зависит только точность поддержания контурной скорости, поэтому число разрядов Δφ можно выбрать из требования постоянства контурной скорости и допустимого углового ускорения, которое определяют допустимым ускорением по координатам и радиусом окружности. Для большинства современных станков число двоичных разрядов Δφ лежит в пределах от шести до восьми. Это существенно сокращает время реализации алгоритма круговой интерполяции.
Оценим методическую ошибку интерполяции, возникающую за счёт неточного вычисления тригонометрических функций в выражении (3.14) по сравнению с выражением (3.13):
(3.15)
где αi +1, βi +1 – вычисленные значения координат; α*i +1, β*i +1 – точные значения координат; δαi +1, δβi +1 – погрешности приближенного вычисления.
Погрешность вычисления можно оценить по первому отбрасываемому члену, так как ряды sinφ и cosφ – знакопеременные:
; 
.
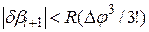На следующем шаге, используя выражения (3.14) и (3.15), получим:
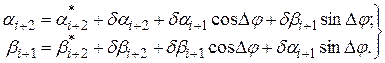
Рис. 3.9. Алгоритм реализации круговой интерполяции методом цифрового интегрирования на участке Δt
Так как значение Δφ мало, то cos Δφ ≈ 1, а sin Δφ ≈ 0. Из этого следует, что накопленная погрешность в вычислении координат не будет превышать NR (Δφ3 /3!), где N – число шагов интегрирования. Это число максимально может составить Nmax = 2π/ Δφ.
Тогда максимальную накопленную погрешность δα∑ по координате определим по формуле
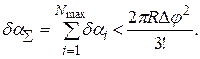(3.16)
Шаг Δφ имеет максимальное значение, равное
, (3.17)
где Vmax – максимальная контурная скорость; Δt – квант интегрирования; Rmin – минимальный радиус дуги. С учётом выражения (3.17) выражение (3.16) будет иметь вид
.
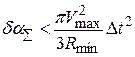Учитывая, что Vmax / Rmin не должно превышать допустимого ускорения а доп по координатам, получим окончательную оценку накопленной ошибки
.
К этой погрешности необходимо добавить погрешность за счёт ошибок округления, которые пропорциональны количеству шагов ввиду малости Δφ в выражении (3.14). Полученные оценки позволяют выбрать разрядность ЭВМ или выработать требования к допустимому ускорению (т. е. к увеличению Rmin) при круговой интерполяции.
Подготовка исходных данных для круговой интерполяции заключается в определении полного угла поворота в плоскости αβ угловых скоростей и ускорения и соответствия абстрактных координат α и β действительным координатам станка по данным, получаемым из управляющей программы. Помимо указания круговой интерполяции и направления движения, обычно задают ещё и координаты центра окружности и конечной точки, а также контурную скорость.
Для определения угловых скоростей ω 0, ω 3, ω к.к, а также углового ускорения ε необходимо вычислить радиус R окружности. Так как ω = V / R; ε = a доп / R то 
, где α н, β н – координаты начальной точки относительно центра окружности.
Погрешности вычисления радиуса и контурного пути не влияют на точность интерполяции, а сказываются только на точности поддержания контурной скорости.
Для вычисления угла поворота необходимо найти начальный и конечный углы и определить их разность: 
, 
.
Следует отметить, что точность вычисления углов определяется максимально допустимым радиусом, так как погрешность в определении контурного пути равна
. (3.18)
Зная значения δφ и Rmax, можно определить необходимую точность вычисления углов.
Для определения момента начала торможения рассчитывается тормозной путь по формуле, аналогичной (3.12), где вместо линейных (контурных) скоростей и ускорений нужно подставить значения угловых скоростей и ускорений. Для исключения броска по скорости при выдаче приращений в конце кадра применяют способ, описанный при рассмотрении линейной интерполяции.
Для линейной и круговой интерполяции (а также любого другого вида интерполяции) методом МЦИ необходим обоснованный выбор шага интегрирования Δt. Значение Δt выбирается исходя из двух соображений. С одной стороны, для улучшения динамики привода желательно взять значение Δt как можно меньше. С другой стороны, для выполнения более сложных алгоритмов, реализующих движение по траекториям сложной формы и имеющих малые ошибки, требуется впол<