1. Индивидуальный индекс - относительная величина, характеризующая изменение во времени каких-либо явлений и определяемая путем деления величины этого явления в отчетном периоде на величину его в базисном периоде.
В общем случае индивидуальный индекс цены определяется по формуле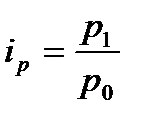 
, где 
и 
–цена продукции в отчетном и базисном периоде. В рассматриваемой задаче не известны цены товара, а дан процент изменения цен в отчетном периоде по сравнению с базисным, таким образом, индивидуальные индексы цен по видам товаров определяются по формуле:
,
где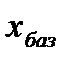 
- база сравнения, которая берется за 100%.
Для приведенного примера индивидуальные индексы цены по каждому виду продукции рассчитываются следующим образом:
яйцо -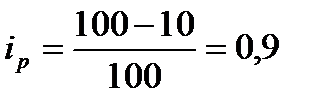 
; мука - 
крупа -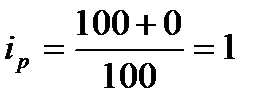 
.
2. Для обобщения относительного изменения показателя в сложной совокупности рассчитываются общие (сводные) индексы. Они характеризуют относительное изменение индексируемой величины в целом по всей совокупности, отдельные элементы которой несоизмеримы в физических единицах.
В зависимости от цели исследования и наличия исходных данных используют различную форму построения общих индексов: агрегатную или среднюю.
При расчете общих индексов показатели, выраженные в различных единицах измерения, приводят к сопоставимому виду с помощью специальных коэффициентов взвешивания. При этом принято следующее соглашение:
− индексы количественных показателей (объема, площади, численности коров) используют в качестве весов значения базисного периода;
− индексы качественных показателей (цены, себестоимости, урожайности, надоя) – значения отчетного периода.
В данном случае для характеристики среднего изменения цен по всем товарам, в качестве веса используется объем проданной продукции в отчетном периоде (
), поэтому индекс цен определяется по формуле:
|
|
,
В примере исходными данными для расчета общего индекса цены являются данные о стоимости товара в отчетном периоде (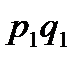
) и рассчитанные индивидуальные индексы цен по каждому товару (
).
В этом случае общий индекс цен как агрегатный определить нельзя, однако можно вычислить его по формуле среднего гармонического из индивидуальных индексов, который легко преобразовывается в формулу агрегатного индекса:
Следовательно, по всему ассортименту товаров цены в отчетном периоде снизились в среднем на 2,5 % (97,5%-100%=-2,5%) по сравнению с базисным.
Результаты проведенных расчетов удобно представить в табличном виде (таблица 14).
Таблица 14 Расчет индивидуальных и общего индексов цен
| Товар | Продано в фактических ценах, тыс. руб. | Изменение цен в отчетном периоде по сравнению с базисным, % | Расчетные значения | |||
| базисный период, p0q0 | отчетный период, p1q1 | Индекс цены, 
| p0q1 | |||
| Яйцо | -10 | 0,90 | 266,67 | |||
| Мука | 1,05 | 209,52 | ||||
| Крупа | без изменений | 170,00 | ||||
| Итого | Х | Х | 646,19 | |||
| Общий индекс цен | 0,975 | |||||
| На рис. 13 представлено проведение расчетов индивидуальных и общего индексов цены продаж по видам продукции в ТП Excel. | |||||
| ||||||
Рисунок 13 Расчет таблицы 9 в ТП Excel
3. Общий индекс изменения физического объема продукции, как показатель количественный, имеет вид:
Объем продаж в целом по всем видам продукции возрос на 15,4 %
|
|
4. Общий индекс товарооборота может быть рассчитан:
− по формуле агрегатного индекса, 
;
− по значениям общих индексов цен и физического объема: 
Товарооборот предприятия увеличился на 12,5 %.
5. Абсолютная величина изменения находится в виде разности числителя и знаменателя соответствующего индекса. Для определения изменения товарооборота, которое вызвано изменением цен на товары, следует рассматривать разность числителя и знаменателя формулы агрегированного индекса цены:
На основании полученного результата можно сделать вывод о том, что товарооборот в отчетном периоде снизился по сравнению с базисным на 16,19 тыс. руб. за счет изменения цен.