Кафедра экономической теории, учета и анализа
СТАТИСТИКА
Методические указания и задания к практическому занятию
по теме «Ряды распределения»
Факультеты: экономический, гуманитарный
Направление подготовки: 38.03.04 ГОСУДАРСТВЕННОЕ И
МУНИЦИПАЛЬНОЕ УПРАВЛЕНИЕ
Профиль подготовки: государственное и муниципальное управление
Направление подготовки: 38.03.02 МЕНЕДЖМЕНТ
Профиль подготовки: управление человеческими ресурсами
Вологда
УДК: 311.13 (076)
Статистика: Методические указания и задания к практическому занятию по теме «Ряды распределения» / Сост.: Л.В. Ярыгина ‑ Вологда: ВоГУ, 2016. – 19 с.
В методических указаниях приводится порядок построения и анализа вариационных рядов Основные положения сопровождаются примерами. Предложены задания для практического закрепления материала. Методические указания предназначены для студентов всех форм обучения.
Утверждено редакционно-издательским советом ВоГУ
Составители: Л.В. Ярыгина, к.э.н., доцент кафедры ЭТУ и А
Рецензент: О.Г. Моронова, к.э.н., доцент кафедры Э и М
ВВЕДЕНИЕ
Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Цель его – выявление основных свойств и закономерностей исследуемой статистической совокупности.
Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определённому варьирующему признаку. Это простая группировка, в которой каждая выделенная группа характеризуется только количеством входящих в неё единиц совокупности (в абсолютном или относительном выражении).
|
|
В зависимости от того, каким является признак, взятый за основу группировки (качественным или количественным)[1], различают два типа рядов распределения: атрибутивные и вариационные.
Ряды распределения, построенные по качественным признакам, называются атрибутивными. (Пример: распределение населения по полу, национальности, профессии и т.д.) Ряды распределения, построенные по количественному признаку, называются вариационными. (Пример: распределение населения по возрасту, сотрудников по стажу работы, домохозяйств по уровню доходов и расходов и т.д.)
В настоящих методических указаниях основное внимание уделяется построению и анализу вариационных рядов.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Атрибутивные ряды
В атрибутивных рядах каждое возможное значение признака регистрируется в виде текстовой записи и указывается соответствующее ему число единиц совокупности либо их доля.
Пример 1. Имеются данные о количестве работников предприятия, находившихся в очередном отпуске, по месяцам года:
| Месяц | Число работников, находившихся в очередном отпуске |
| Январь | |
| Февраль | |
| Март | |
| Апрель | |
| Май | |
| Июнь | |
| Июль | |
| Август | |
| Сентябрь | |
| Октябрь | |
| Ноябрь | |
| Декабрь | |
| Итого |
Данный ряд распределения позволяет выявить некоторую закономерность, а именно, тот факт, что большая часть работников предпочитает для очередного отпуска летний период.
Вариационные ряды
Величины количественного признака у отдельных единиц совокупности более или менее различаются между собой. Такое различие величины признака называется вариацией. Числовые значения признака, встречающиеся в данной совокупности, называют вариантами значений. (Обозначаются малыми буквами конца латинского алфавита – xi, yj, zk. Далее в методических указаниях ‑ xi.)
|
|
Данные о значении признака у отдельных единиц совокупности (данные статистического наблюдения) обычно представляют собой множество расположенных в беспорядке чисел, так называемый первичный ряд. При наличии достаточно большого количества значений признака первичный ряд трудно обозрим, и непосредственное рассмотрение его не даёт представления о распределении единиц по величине признака в совокупности. Выполняется ранжирование первичного ряда, т.е. расположение всех наблюдаемых значений признака в порядке неубывания (невозрастания).
Пример 2. Имеются данные о ежедневном количестве выданных ипотечных кредитов банком N в рабочие дни месяца: 2, 1, 3, 4, 0, 5, 4, 4, 6, 3, 2, 2, 3, 4, 5, 5, 6, 7, 1, 3, 4, 5, 4. Ранжированный ряд: 0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 7.
Варианты значений признака у отдельных единиц могут повторяться. Число повторений отдельных вариантов называют частотой повторения или весом. (Веса обозначаются mi.) Можно рассчитать относительную частоту каждого варианта – частость. (Обозначаются di. di=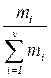 
, 
.) Частости могут быть выражены в долях единиц или %.
По характеру вариации значений признаки делятся на дискретные и непрерывные. Дискретные признаки отличаются друг от друга на некоторую конечную величину, т.е. даны в виде прерывных чисел. (Пример: число членов семьи, количество этажей здания, комнат в квартире и т.д.) Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину и в определённых границах принимать любые значения. (Пример: рост, вес человека, размер заработной платы и т.д.)
|
|
Для дискретного признака, принимающего небольшое число вариантов значений, стоится дискретный вариационный ряд. Дискретным вариационным рядом называется ранжированная совокупность вариантов xi с соответствующими им частотами mi или частостями di. Такой ряд распределения принято оформлять в виде таблицы:
| Варианты (xi) | x1 | x2 | … | xv |
| Частоты (mi) | m1 | m2 | … | mv |
| Частости (di) | d1 | d2 | … | dv |
Пример 3. По данным примера 2 построить дискретный вариационный ряд. Признак «Ежедневное количество ипотечных кредитов, выданных банком» является дискретным. Варианты значений признака – 0, 1, 2, 3, 4, 5, 6, 7. Веса вариантов – 1, 2, 3, 4, 6, 4, 2, 1 соответственно. Также можно определить частости вариантов: 
, 
, 
, 
, 
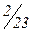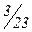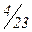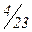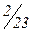, , , , где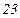 
‑ сумма всех частот. Таким образом, получается следующий вариационный ряд:
| Ежедневное количество ипотечных кредитов, выданных банком (xi) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Число рабочих дней месяца (mi) | 1 | 2 | 3 | 4 | 6 | 4 | 2 | 1 |
| Доля рабочих дней месяца (di) |
|
|
|
|
|
|
|
|
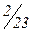
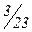
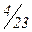
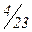
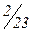
Видно, что в основном банк N в день выдаёт от 3 до 5 ипотечных кредитов.
Если число вариантов дискретного признака велико, а также при анализе вариации непрерывного признака, строятся интервальные ряды распределения. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений признака с соответствующими частотами (частостями) попадания в каждый из них значений признака. Интервальный вариационный ряд можно представить в виде таблицы:
| Интервалы | α1‑ α2 | α2‑α3 | … | αv‑αv+1 |
| Частоты (mi) | m1 | m2 | … | mv |
| Частости (di) | d1 | d2 | … | dv |
Такие ряды распределения наиболее распространены в практике статистической работы.
При построении интервальных вариационных рядов необходимо установить число групп (частичных интервалов), на которые следует разбить все единицы изучаемой совокупности, и определить их границы. Каждый интервал имеет нижнююграницу (наименьшее значение признака в группе) и верхнююграницу (наибольшее значение признака в группе). Величинаинтервала представляет собой разность между его верхней и нижней границами. (Обозначается hi.) Интервал, который имеет обе границы, называется закрытым. Интервал, в котором указана лишь одна граница (верхняя или нижняя), называется открытым. Открытыми могут быть первый и последний интервалы. (Первый интервал не имеет нижней границы, а последний – верхней.) Такие интервалы могут быть условно закрыты. При этом предполагается, что величина первого интервала равна величине второго, а величина последнего – величине предпоследнего. Также интервалы могут быть равными и неравными.
Пример 4. Проводились наблюдения суммы дневной выручки в магазине детских товаров в период распродажи по сниженным ценам. Были получены следующие результаты*:
| Дневная выручка, д.е. | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 |
| Число дней (mi) | 3 | 5 | 9 | 14 | 8 | 3 |
| * ‑ Верхние границы частичных интервалов открытые. |
В данном случае интервалы значений признака закрытые и равные. Величина интервала – 200 д.е. Из приведённого вариационного ряда видно, что в период распродажи дневная выручка магазина в основном составляла от 300 до 600 д.е.
При группировке внутри однокачественных совокупностей появляется возможность применения равных интервалов. Определение величины интервала h для вариационного ряда с равными интервалами производится следующим способом:
1. Устанавливается размах варьирования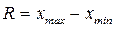 
.
2. Выбирается число интервалов v (обычно от 7 до 11). Можно использовать формулу Стэрджесса:
,
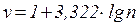где n ‑ численность изучаемой совокупности.
3. Вычисляется h по формуле: h 
. Если h дробное число, то за длину частичного интервала следует брать ближайшее целое число или ближайшую простую дробь.
За начало первого частичного интервала рекомендуется брать величину α1 = xmin – 0,5h. Конец последнего частичного интервала должен удовлетворять условию αv+1 –h ≤ xmax < αv+1. Остальные границы получаются прибавлением к нижней границе частичного интервала величины h.
Далее просматривая результаты наблюдений, можно определить, сколько значений признака попадает в каждый частичный интервал. При этом в конкретный интервал включаются значения, ≥ нижней границы и < верхней (или наоборот).
Неравные интервалы применяются при группировках, которые охватывают массу единиц неоднородной совокупности с неравномерными и значительными колебаниями изучаемого признака. В типологической группировке, производимой по количественному признаку, границы, отделяющие друг от друга качественные типы, не являются произвольными. Они должны удовлетворять значениям, в которых количественные изменения переходят в новое качество. В случаях значительной вариации группировочного признака применяются кратные интервалы. Обычно используются удвоенные кратные интервалы, т.е. величина каждого последующего интервала по сравнению с предыдущим удваивается. (Интервалы группировки считаются обоснованными, если коэффициент вариации признака в них не превышает 33 %.)
Для интервальных вариационных рядов с неравными интервалами важную роль играет частота (частость), приходящаяся на единицу величины интервала, ‑ плотность распределения. (Обозначается fi.) Абсолютная плотность распределения ‑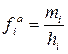 
, относительная ‑ 
.
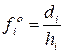Интервальный вариационный ряд можно условно заменить дискретным. Для этого срединное значение i -го частичного интервала принимается за вариант xi, а соответствующая интервальная частота mi – за частоту этого варианта.
Иногда нужно знать, сколько значений признака не превышают заданного значения X. Для этого используется понятие накопленной частоты или частости. (Накопленные частоты обозначаются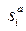 
, накопленные частости ‑ 
.) Накопленной частотой (частостью), соответствующей варианту xi, называется общее число вариантов (их доля), имеющих значения признака, ≤ данному, т.е. для которых X ≤ xi. Накопленной частотой (частостью) частичного интервала является сумма частот (частостей) всех предшествующих интервалов и данного.
Пример 5. По данным примера 4 рассчитать накопленные частоты. В данном случае имеется интервальный вариационный ряд. Накопленная частота первого частичного интервала равна частоте этого интервала, т.е. 3, накопленная частота второго частичного интервала равна сумме частот первых двух интервалов: 3+5=8. И т.д. Накопленная частота последнего частичного интервала равна сумме всех частот. Таким образом, имеем:
| Дневная выручка, д.е. | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 |
| Число дней (mi) | 3 | 5 | 9 | 14 | 8 | 3 |
Накопленные частоты ( )
| 3 | 8 | 17 | 31 | 39 | 42 |
Накопленная частота третьего частичного интервала указывает, что в 17 дней распродажи сумма дневной выручки магазина детских товаров была меньше 400 д.е.
Графическое изображение вариационных рядов
Наглядное представление о закономерностях варьирования наблюдаемых значений признака помогает получить графическое изображение вариационного ряда.
Для изображения дискретного вариационного ряда строится полигон распределения. На оси абсцисс откладываются значения вариантов, на оси ординат – соответствующие частоты или частости. Полученные точки соединяются отрезками прямой линии.
Для изображения интервального вариационного ряда строится гистограмма. На оси абсцисс откладываются отрезки, отражающие частичные интервалы варьирования, и на них, как на основаниях, строятся прямоугольники, высоты которых равны соответствующим интервальным частотам или частостям. (Получается ступенчатая фигура из прямоугольников.) Если интервальный вариационный ряд преобразовать в дискретный, то для его изображения можно построить полигон распределения (середины верхних сторон прямоугольников соединяются отрезками прямой линии).
Пример 6. По данным примеров 3, 4 построить графики вариационных рядов. Для изображения дискретного вариационного ряда применяется полигон (рисунок 1), а интервального – гистограмма (рисунок 2).
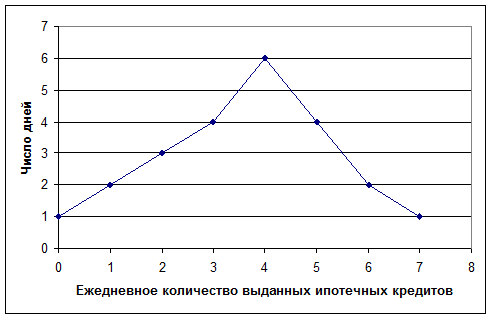
Рисунок 1. Полигон для данных примера 3
Рисунок 2. Гистограмма и полигон для данных примера 4
Интервальный вариационный ряд из примера 4 можно условно преобразовать в дискретный:
| Дневная выручка, д.е. (xi) | 150 | 250 | 350 | 450 | 550 | 650 |
| Число дней (mi) | 3 | 5 | 9 | 14 | 8 | 3 |
и построить полигон (рисунок 2).
При изображении вариационного ряда с накопленными частотами используется кумулятивная кривая (кумулята). Для построения кумуляты дискретного вариационного ряда на оси абсцисс наносятся варианты, на оси ординат – накопленные частоты или частости. Полученные точки соединяются прямыми отрезками. Для построения кумуляты интервального вариационного ряда нижней границе первого частичного интервала ставится в соответствие частота или частость, равная 0, а верхней – вся частота или частость этого интервала. Верхней границе второго частичного интервала соответствует накопленная частота или частость по первым двум интервалам и т.д., верхней границе последнего частичного интервала соответствует накопленная частота или частость, равная сумме всех частот или частостей.
Огива вариационного ряда строится аналогично кумуляте с той лишь разницей, что на оси абсцисс наносятся накопленные частоты или частости, а на оси ординат – варианты или частичные интервалы.
Пример 7. По данным примера 5 построить кумуляту и огиву. Соответствующие графики представлены на рисунках 3, 4.
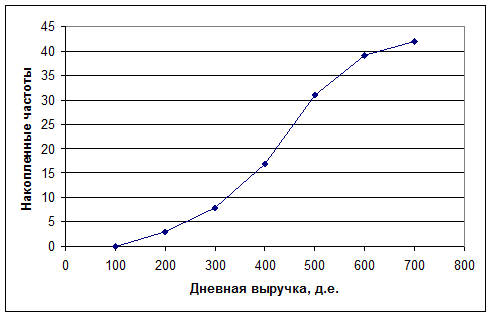
Рисунок 3. Кумулята по данным примера 5
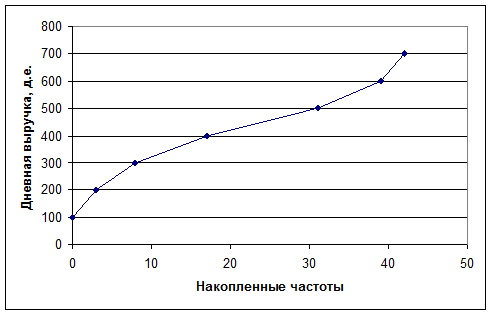
Рисунок 4. Огива по данным примера 5