Числовые характеристики вариационного ряда

Построив вариационный ряд и изобразив его графически, можно получить первоначальное представление о закономерностях, имеющих место в ряду наблюдений. Для дальнейшего изучения изменения значений признака используются числовые характеристики вариационного ряда. Основные характеристики вариационного ряда можно разбить на три группы: 1) показатели центра распределения, 2) показатели вариации, 3) показатели формы распределения.

Показатели центра распределения

Характеристиками центра распределения данных вариационного ряда являются средняя арифметическая, медиана и мода.

Средней арифметической наблюдаемых значений признака называется частное от деления суммы всех этих значений на их число, т.е. . (Вычисленная по этой формуле средняя арифметическая называется простой).

Если данные наблюдений представлены в виде дискретного вариационного ряда, то или 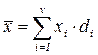. (В этих случаях средняя арифметическая называется взвешенной.)

Для определения среднего значения признака интервального вариационного ряда необходимо его условно заменить дискретным, а затем воспользоваться формулой средней арифметической взвешенной. Понятно, что в случае неравномерного распределения значений признака внутри частичных интервалов, полученное значение средней арифметической может отличаться от рассчитанного по несгруппированным данным.

Медиана () – значение признака в середине вариационного ряда.

Для определения медианы дискретного вариационного ряда вначале необходимо найти её позицию по формуле . Этой позиции и соответствует значение медианы. Оно может быть вариантом ряда или промежуточным значением между двумя соседними вариантами.

Для расчёта медианы интервального вариационного ряда вначале определяется медианный интервал: 1) просматриваются накопленные частоты, 2) первая из накопленных частот, превышающая половину всего объёма изучаемой совокупности, соответствует медианному интервалу. Далее значение медианы вычисляется по формуле:

,

где ‑ длина медианного интервала;

‑ нижняя граница медианного интервала;

‑ частота медианного интервала;

– накопленная частота интервала, предшествующего медианному.

Мода () – значение признака, наиболее часто встречающееся в вариационном ряду.

Мода дискретного вариационного ряда соответствует варианту с наибольшей частотой.

Для определения моды интервального вариационного ряда вначале устанавливается модальный интервал: если рассматривается интервальный вариационный ряд с равными интервалами, то модальный интервал определяется по наибольшей частоте; если рассматривается интервальный вариационный ряд с неравными интервалами, то модальный интервал определяется по наибольшей плотности распределения. Далее мода рассчитывается по формуле:

,

где ‑ длина модального интервала;

‑ нижняя граница модального интервала;

, , ‑ частота модального интервала, частота интервала, предшествующего модальному, и частота интервала, следующего за модальным.

Средняя арифметическая имеет существенные преимущества перед другими мерами центральной тенденции, т.к. основывается на информации, содержащей все значения вариационного ряда. Однако, она весьма чувствительна к крайним значениям ряда. Поэтому, если необходимо предотвратить влияние нескольких наблюдений, расположенных далеко от центра распределения, то следует использовать медиану. Моде отдаётся предпочтение при изучении цен на рынке, спроса населения на некоторые продукты питания, одежду и обувь определённых размеров.

 

Пример 8. По данным примера 3 определить меры центральной тенденции.

Для дискретного вариационного ряда среднее значение признака вычисляется по формуле средней арифметической взвешенной, т.е.

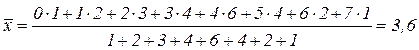или

В среднем банк N выдавал в день по 3,6 ипотечных кредита.

Позиция медианы данного вариационного ряда соответствует 12 значению признака в ранжированном ряду (). Таким образом, (смотри пример 2). Это значит, что срединное значение количества ипотечных кредитов, выданных в день банком N, равно 4.

Мода дискретного вариационного ряда определяется по варианту с наибольшей частотой. Следовательно, . Наиболее часто банк N выдавал в день по 4 ипотечных кредита.

Пример 9. По данным примера 4 определить меры центральной тенденции.

Для определения среднего значения признака интервального вариационного ряда сначала необходимо условно заменить его дискретным (смотри пример 6). Далее можно использовать формулу средней арифметической взвешенной:

.

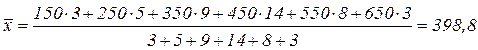В период распродажи по сниженным ценам средняя сумма дневной выручки в магазине детских товаров составила 398,8 д.е.

Вычисление медианы интервального вариационного ряда начинается с установления медианного интервала. Сумма всех частот равна 42. Первая из накопленных частот, превышающая половину объёма изучаемой совокупности, соответствует интервалу от 400 до 500 д.е. (смотри пример 5). Следовательно, . Срединное значение суммы дневной выручки в магазине детских товаров в период распродажи составило 428,6 д.е.

Для определения моды интервального вариационного ряда вначале выбирается модальный интервал. Так как рассматривается интервальный вариационный ряд с равными интервалами, то модальный интервал устанавливается по наибольшей частоте. Наибольшая частота, равная 14, соответствует интервалу от 400 до 500 д.е. Значение моды составляет . Наиболее часто встречавшаяся сумма дневной выручки магазина детских товаров в период распродажи ‑ 445,5 д.е.

Показатели вариации

В статистике используется ряд мер вариабельности (колеблемости).

Размах вариации – разность между наибольшим и наименьшим вариантами .

Размах вариации – показатель разброса значений признака в наборе данных. Однако больший интерес представляют показатели рассеяния наблюдаемых значений признака вокруг средней арифметической.

Средним линейным отклонением вариационного ряда называется средняя арифметическая абсолютных величин отклонений наблюдаемых значений признака от их средней арифметической . Если данные наблюдений представлены в виде дискретного вариационного ряда, то .

Дисперсией вариационного ряда называется средняя арифметическая квадратов отклонений наблюдаемых значений признака от средней арифметической . Если же данные наблюдений представлены в виде дискретного вариационного ряда, то . Именно этот показатель чаще всего используется для характеристики рассеяния наблюдаемых значений признака вокруг средней арифметической. Вместе с тем дисперсия обладает одним существенным недостатком: выражается в квадратных единицах. Поэтому применяется ещё один показатель – среднее квадратическое отклонение, который определяется как арифметический квадратный корень из дисперсии и имеет ту же размерность, что и изучаемый признак. Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойством мажорантности средних.

Рассмотренные показатели являются абсолютными мерами рассеяния вариантов ряда. В некоторых случаях используются и относительные меры рассеяния, например, коэффициент вариации. Он представляет собой отношение среднего квадратического отклонения к средней арифметической:

.

Чем меньше коэффициент вариации, тем однороднее совокупность, тем точнее средняя отражает значения изучаемого признака.

 

Пример 10. По данным примера 3 рассчитать показатели вариации.

Размах вариации (ипотечных кредитов).

Среднее линейное отклонение составило

(ед.).

Дисперсия равна

(ед.²).

Среднее квадратическое отклонение ‑ (ед.).

Наконец, коэффициент вариации ‑ .

Видно, что индивидуальные значения признака отличаются в среднем от среднего арифметического на 1,7 кредита, или на 47,2 %. Полученные значения показателей вариации позволяют сделать вывод о значительной вариации количества выданных ипотечных кредитов банком N в рабочие дни месяца.

Показатели формы распределения

Под формой статистического распределения понимается форма графика вариационного ряда – полигона или гистограммы. Формы графиков могут быть разнообразными. Прежде всего, они делятся на симметричные и несимметричные (асимметричные). Распределение называется симметричным, если частоты любых вариантов, равностоящих от среднего, равны между собой. При изучении экономических явлений чаще встречаются асимметричные распределения.

Умеренно асимметричными называются распределения, в которых частоты, находящиеся по одну сторону от наибольшей, больше (или меньше) частот, находящихся по другую сторону от наибольшей на том же расстоянии. Асимметрия может быть левосторонняя и правосторонняя. Прилевостороннейасимметрии частоты сначала медленно возрастают, а затем очень быстро убывают. Приправосторонней – наоборот.

Для характеристики асимметрии применяются разные показатели. Наиболее распространённым является показатель, основанный на определении центрального момента третьего порядка . В симметричных вариационных рядах равен 0, при < 0 имеет место левосторонняя асимметрия, при > 0 – правосторонняя. Нормированный момент третьего порядка называется коэффициентом асимметрии . Асимметрия считается существенной, если по модулю больше 0,5.

Графики вариационных рядов могут быть низковершинными и высоковершинными. Имеется в виду выпад вершины эмпирического распределения вниз или вверх от вершины кривой нормального распределения.

Показатели эксцесса рассчитываются для симметричных распределений. Наибольшее распространение имеет коэффициент эксцесса , где ‑ нормированный момент четвёртого порядка. Для нормального распределения , следовательно, при = 0 распределение нормальное, при < 0 – низковершинное, при > 0 – высоковершинное.

 

Пример 11. По данным примера 3 вычислить показатели формы распределения.

Как видно на рисунке 1 распределение рабочих дней месяца по количеству выданных ипотечных кредитов несимметрично. О существенности асимметрии позволяет судить значение коэффициента асимметрии. Для его определения сначала вычисляется центральный момент третьего порядка:

.

Коэффициент асимметрии ‑ . Следовательно, в данном ряду распределения асимметрия левосторонняя, несущественная.

Можно рассчитать коэффициент эксцесса. В первую очередь определяется центральный момент четвёртого порядка:

.

Далее вычисляется коэффициент эксцесса ‑ 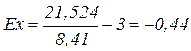. Таким образом, изучаемое распределение низковершинное.

ЗАДАНИЯ К ВЫПОЛНЕНИЮ

По данным задач 1 и 2 требуется:

1) Построить вариационный ряд и изобразить его графически.

2) Определить меры центральной тенденции.

3) Рассчитать показатели вариации и прокомментировать полученные значения.

4) Вычислить показатели асимметрии и эксцесса и сделать вывод о форме распределения.

 

Задача 1.

 

Вариант 0.

 

В отделе дамской обуви универмага в течение дня были проданы туфли следующих размеров: 37, 35, 36, 37, 38, 37, 36, 37, 39, 38, 37, 36, 37, 37, 36.

 

Вариант 1.

 

На телефонной станции в течение часа проводились наблюдения за числом неправильных соединений в минуту. Были получены следующие результаты: 3, 1, 3, 1, 4, 2, 2, 4, 0, 3, 0, 2, 2, 0, 2, 1, 4, 3, 3, 1, 4, 2, 1, 1, 2, 1, 0, 3, 4, 1, 3, 2, 7, 2, 0, 0, 1, 3, 3, 1, 2, 4, 2, 0, 2, 3, 1, 2, 5, 1, 1, 0, 1, 1, 2, 2, 1, 5, 2, 3.

 

Вариант 2.

 

Администрацию универсама интересуют среднемесячные объёмы покупок товаров, которые не являются предметом ежедневного потребления. В течение января менеджер универсама регистрировал частоту покупок 100-граммовых пакетов с содой и собрал следующие данные: 8, 4, 4, 9, 3, 3, 1, 2, 0, 4, 2, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 1, 0, 8.

 

Вариант 3.

 

Наблюдения за числом изготовленных в течение смены деталей рабочими цеха дали следующие результаты: 21, 23, 20, 24, 24, 25, 21, 22, 23, 23, 24, 24, 24, 25, 22, 23, 24, 24, 22, 22, 23, 23, 23, 24, 25, 23, 24.

 

Вариант 4.

 

Чтобы выяснить, какие суммы (руб.) тратят студенты второго курса в течение дня, питаясь в кафе университета, проведён опрос 27 случайно отобранных студентов. Были получены следующие результаты:16, 12, 15, 15, 23, 9, 15, 13, 14, 14, 21, 15, 14, 17, 27, 15, 16, 12, 16, 19, 14, 16, 17, 13, 14, 14, 19.

 

Вариант 5.

 

В отделе мужской обуви универмага в течение дня были проданы ботинки следующих размеров: 39, 38, 40, 41, 41, 42, 39, 43, 42, 40, 40, 41, 42, 41, 42, 41, 43.

 

Вариант 6.

 

Тарифные разряды рабочих цеха: 4, 3, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 4, 4, 5, 2, 3, 6, 5, 4, 2, 4, 3.

 

Вариант 7.

 

Имеются следующие данные о размере семьи работников цеха (число человек в семье): 3, 4, 5, 2, 3, 6, 4, 2, 5, 3, 4, 2, 7, 3, 3, 6, 2, 3, 8, 5, 6, 7, 3, 4, 5, 4, 3, 3, 4.

 

Вариант 8.

 

Тарифные разряды рабочих цеха: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.

 

Вариант 9.

 

Дневная производительность труда рабочих бригады, выполняющих одинаковую операцию по обработке детали № 408, следующая (шт.): 19, 18, 20, 20, 21, 22, 21, 19, 23, 22, 22, 20, 21, 20, 23, 21, 20, 21, 20, 19.

 

Задача 2.

 

Для оценки качества выпускаемых изделий замеряли диаметр валиков после шлифовки. Были получены следующие результаты (мм)^**

 

6,75	6,77	6,77	6,73	6,76	6,74	6,70	6,75	6,71	6,72	6,77	6,79	6,71	6,78
6,73	6,70	6,73	6,77	6,75	6,74	6,71	6,70	6,78	6,76	6,81	6,69	6,80	6,80
6,77	6,68	6,74	6,70	6,70	6,74	6,77	6,83	6,76	6,76	6,82	6,77	6,71	6,74
6,77	6,75	6,74	6,75	6,77	6,72+0,01N	6,74	6,80	6,75	6,80	6,72	6,78	6,70	6,75
6,78	6,78	6,76	6,77	6,74	6,74	6,77	6,73	6,74	6,77	6,74	6,75	6,74	6,76
6,76	6,74	6,74	6,74	6,74	6,76	6,74	6,72	6,80	6,76	6,78	6,73	6,70	6,76
6,76	6,77	6,75	6,78	6,72	6,76	6,78	6,68	6,75	6,73	6,82	6,73	6,80	6,81
6,71	6,82	6,77	6,80	6,80	6,70	6,70	6,82	6,72	6,69	6,73	6,76	6,74	6,77
6,72	6,76	6,78	6,78	6,73	6,76	6,80	6,76	6,72	6,76	6,76	6,70	6,73	6,75
6,77	6,77	6,70	6,81	6,74	6,73	6,77	6,74	6,78	6,69	6,74	6,71	6,76	6,76
6,77	6,70	6,81	6,74	6,74	6,77	6,75	6,80	6,74	6,76	6,77	6,77	6,81	6,75
6,78	6,73	6,76	6,76	6,76	6,77	6,76	6,80	6,77	6,74	6,77	6,72	6,75	6,76
6,77	6,81	6,76	6,76	6,76	6,80	6,74	6,80	6,74	6,73	6,75	6,77	6,74	6,76
6,77	6,77	6,75	6,76	6,74	6,82	6,76	6,73	6,74	6,75	6,76	6,72	6,78	6,72
6,76	6,77	6,75	6,78

 

**N – номер варианта

ЛИТЕРАТУРА

1. Аскеров, П.Ф. Общая и прикладная статистика: учебник для студентов вузов, обучающихся по направлению "Статистика" и другим экономическим специальностям / П.Ф. Аскеров, Р.Н. Пахунова, А.В. Пахунов. ‑ Москва: ИНФРА-М, 2014. – 272 с.

2. Ефимова, М.Р. Общая теория статистики: учеб. для вузов по специальностям: финансовый менеджмент, бухгалт. учёт и аудит, междунар. экон. отношения / М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцев. ‑ 2-е изд., испр. и доп. ‑ Москва: ИНФРА-М, 2009. – 416 с.

3. Общая теория статистики: учебник для вузов / под ред. М.Г. Назарова. ‑ Москва: Омега-Л, 2010. – 410 с.

4. Статистика: учебник для бакалавров / под общ. ред. Л. И. Ниворожкиной. ‑ Москва: Дашков и К, 2011. – 415 с.

5. Общая теория статистики: методическое пособие по выполнению практических работ. Часть I / cост.: Н.А. Никитина. ‑ Вологда: ВоГТУ, 2009. – 63 с.

6. Годин, А.М. Статистика [Электронный ресурс]: учебник для бакалавров / А.М. Годин. ‑ 11-е изд., перераб. и испр. – Москва: Дашков и Ко, 2014. – 412 с. Режим доступа: https://biblioclub.ru/index.php?page=book&id=253808.

7. Гусаров, В.М. Статистика [Электронный ресурс]: учебное пособие / В.М. Гусаров, Е.И. Кузнецова. ‑ 2-е изд., перераб. и доп. ‑ Москва: Юнити-Дана, 2012. – 480 с. Режим доступа: https://biblioclub.ru/index.php?page=book&id=117190.

8. Никифорова, Н.Г. Статистика: теория и практика в Excel [Электронный ресурс]: учебное пособие / Н.Г. Никифорова, В.С. Лялин, И.Г. Зверева. ‑ Москва: Финансы и статистика, 2010. – 448 с. Режим доступа: https://biblioclub.ru/index.php?page=book&id=78916.

9. Улитина, Е.В. Статистика [Электронный ресурс]: учебное пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова; под ред. Е.В. Улитиной. ‑ 3-е изд., стер. ‑ Москва: Московский финансово-промышленный университет «Синергия», 2013. – 320 с. Режим доступа: https://biblioclub.ru/index.php?page=book&id=252966.

10. Шелобаева, И.С. Статистика [Электронный ресурс]: практикум: учебное пособие / И.С. Шелобаева, С.И. Шелобаев. ‑ 2-е изд., перераб. и доп. ‑ Москва: Юнити-Дана, 2012. – 208 с. Режим доступа: https://biblioclub.ru/index.php?page=book&id=119522.

[1] Количественные признаки – такие свойства общественных явлений, которые различаются их численными значениями. Качественны е – признаки, колеблемость которых по единицам статистической совокупности выражает черты содержательных (сущностных) различий.