ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
9.1. F-распределение и проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей.
9.2. Проверка гипотезы о равенстве статистической оценки дисперсии  и дисперсии
и дисперсии 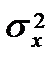 генеральной совокупности.
генеральной совокупности.
9.3. Проверка гипотезы о равенстве средних по двум выборкам из нормальных совокупностей.
9.4. Проверка гипотезы о равенстве статистической оценки математического ожидания заданному значению по выборке из нормальной генеральной совокупности.
9.5. Проверка гипотезы об однородности ряда дисперсий по выборкам различного объема. Критерий Бартлетта.
9.6. Проверка гипотезы об однородности ряда дисперсий по выборкам одинакового объема. Критерий Кохрана.
9.7. Проверка гипотез о вероятности в случае биномиального распределения.
9.8. Проверка гипотез об однородности ряда вероятностей в случае полиномиального распределения.
9.9. Проверка гипотезы о виде закона распределения.
9.10. Оценка сомнительных результатов.
Задачи для самостоятельного решения
9.1. По результатам 8 замеров установлено, что среднее время изготовления детали 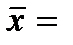 48 с. Предполагая, что время изготовления есть нормальная случайная величина с
48 с. Предполагая, что время изготовления есть нормальная случайная величина с  3 с, необходимо:
3 с, необходимо:
а) проверить на уровне значимости  0,01 гипотезу
0,01 гипотезу  50 c. против конкурирующей гипотезы
50 c. против конкурирующей гипотезы  45 с.;
45 с.;
б) вычислить мощность критерия;
в) проверить на уровне значимости  0,01 гипотезу
0,01 гипотезу  50 c. против конкурирующей гипотезы
50 c. против конкурирующей гипотезы  50 c.
50 c.
9.2. На контрольных испытаниях  16 ламп было определено
16 ламп было определено 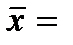 297 ч. Считая, что срок службы ламп распределен нормально с
297 ч. Считая, что срок службы ламп распределен нормально с  20 ч, необходимо:
20 ч, необходимо:
а) проверить на уровне значимости  0,05 гипотезу
0,05 гипотезу  300 ч против конкурирующей гипотезы
300 ч против конкурирующей гипотезы  290 ч;
290 ч;
б) вычислить мощность критерия;
в) на уровне значимости  0,08 проверить гипотезу
0,08 проверить гипотезу  300 ч при конкурирующей гипотезе
300 ч при конкурирующей гипотезе  300 ч.
300 ч.
9.3. В таблице приведены данные об урожайности пшеницы на 8 опытных участках одинакового размера.
| Участки | ||||||||
| Урожайность (ц/га) | 26,5 | 25,2 | 28,9 | 30,1 | 32,3 | 29,3 | 26,1 | 25,0 |
Предполагается, что урожайность пшеницы есть нормальная случайная величина. Требуется:
а) на уровне значимости  0,1 проверить гипотезу
0,1 проверить гипотезу  28 ц/га против конкурирующей гипотезы
28 ц/га против конкурирующей гипотезы  30 ц/га;
30 ц/га;
б) по условию а) вычислить мощность критерия;
в) проверить на уровне значимости  0,002 гипотезу
0,002 гипотезу  29 ц/га против конкурирующей гипотезы
29 ц/га против конкурирующей гипотезы  29 ц/га.
29 ц/га.
9.4. При обработке данных 7 испытаний пограничного катера получены следующие значения его максимальной скорости: 38, 49, 42, 46, 45, 41, 39 км/ч. Полагая, что максимальная скорость катера имеет нормальное распределение, проверить на уровне значимости 0,05 гипотезу  45 км/ч:
45 км/ч:
а) при конкурирующей гипотезе  40 км/ч,
40 км/ч,
б) при конкурирующей гипотезе  45 км/ч;
45 км/ч;
в) по условию а) задачи вычислить мощность критерия.
9.5. По данным 12 рейсов установлено, что в среднем машина затрачивает на поездку до склада боеприпасов  73 мин. Допустив, что время поездки есть нормальная случайная величина, на уровнях значимости 0,05 и 0,1 проверить гипотезу
73 мин. Допустив, что время поездки есть нормальная случайная величина, на уровнях значимости 0,05 и 0,1 проверить гипотезу  75 мин:
75 мин:
а) при конкурирующей гипотезе  72 мин, если известно, что
72 мин, если известно, что  4 мин;
4 мин;
б) при конкурирующей гипотезе  72 мин, если выборочное среднее квадратическое отклонение равно
72 мин, если выборочное среднее квадратическое отклонение равно  4 мин;
4 мин;
в) для условий а) и б) вычислить мощность критерия.
9.6. При 7 независимых измерениях диаметра поршня одним и тем же прибором получены следующие результаты: 82,45; 82,30; 82,48; 82,05; 82,45; 82,60; 82,46 мм. В предположении, что ошибки измерений имеют нормальное распределение и не содержат систематической ошибки на уровнях значимости 0,05 и 0,2, проверить гипотезу  0,02 мм2:
0,02 мм2:
а) при конкурирующей гипотезе  0,05 мм2;
0,05 мм2;
б) при конкурирующей гипотезе 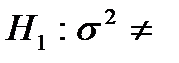 0,02 мм2;
0,02 мм2;
в) при конкурирующей гипотезе  > 0,02;
> 0,02;
г) для условия а) вычислить мощность критерия.
9.7. На основании 12 измерений найдено, что средняя высота сальниковой камеры равна 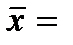 67 мм и
67 мм и 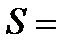 0,7 мм. Допустив, что ошибка изготовления есть нормальная случайная величина, на уровне значимости 0,01 проверить гипотезу
0,7 мм. Допустив, что ошибка изготовления есть нормальная случайная величина, на уровне значимости 0,01 проверить гипотезу  0,5 мм2:
0,5 мм2:
а) при конкурирующей гипотезе  0,1 мм2;
0,1 мм2;
б) при конкурирующей гипотезе 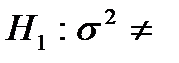 0,5 мм2;
0,5 мм2;
в) при конкурирующей гипотезе  >0,5 мм2;
>0,5 мм2;
г) по условию а) задачи вычислить мощность критерия.
9.8. Точность работы автоматической линии проверяют по дисперсии контролируемого признака, которая не должна превышать  0,11. По результатам выборочного контроля получены следующие данные:
0,11. По результатам выборочного контроля получены следующие данные:
Контролируемый размер 
| 63,0 | 63,5 | 63,8 | 64,4 | 64,6 |
Частота 
|
Требуется проверить на уровне значимости 0,01, обеспечивает ли линия требуемую точность.
9.9. Из продукции двух автоматических линий, обрабатывающих корпуса вентилей одного типоразмера, взяты выборки объемом соответственно  14 и
14 и 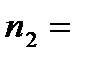 9 корпусов. По результатам выборочных наблюдений найдено
9 корпусов. По результатам выборочных наблюдений найдено  182 мм,
182 мм,  185 мм. Предварительно установлено, что погрешности изготовления есть нормальные случайные величины с дисперсиями
185 мм. Предварительно установлено, что погрешности изготовления есть нормальные случайные величины с дисперсиями 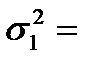 5 мм2 и
5 мм2 и  7 мм2. Требуется на уровнях значимости 0,025 и 0,075 проверить гипотезу
7 мм2. Требуется на уровнях значимости 0,025 и 0,075 проверить гипотезу 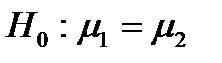 :
:
а) при конкурирующей гипотезе  ;
;
б) при конкурирующей гипотезе 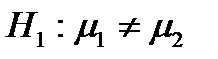 .
.
9.10. По двум независимым выборкам объемом  25 и
25 и 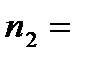 12, извлеченным неформальных генеральных совокупностей, найдены выборочные средние
12, извлеченным неформальных генеральных совокупностей, найдены выборочные средние  1350 и
1350 и  1375. Дисперсии генеральных совокупностей известны -
1375. Дисперсии генеральных совокупностей известны - 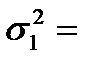 120 и
120 и  100. На уровне значимости 0,01 проверить нулевую гипотезу
100. На уровне значимости 0,01 проверить нулевую гипотезу 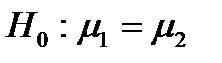 при конкурирующей гипотезе
при конкурирующей гипотезе 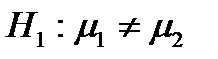 .
.
9.11. Расход сырья на единицу продукции по старой технологии составил:
Расход сырья 
| |||
Число изделий 
|
Расход сырья по новой технологии составил:
Расход сырья 
| ||||
Число изделий 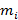
|
Предположив, что расходы сырья в обоих случаях есть нормальные случайные величины с одинаковыми средними квадратическими отклонениями и генеральными средними  и
и  , проверить на уровне значимости 0,1 нулевую гипотезу
, проверить на уровне значимости 0,1 нулевую гипотезу 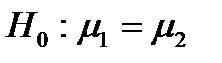 против конкурирующей гипотезы: а)
против конкурирующей гипотезы: а) 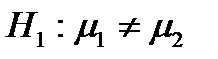 ; б)
; б)  .
.
9.12. Из продукции двух станков-автоматов, выпускающих однотипные изделия, взяты выборки объемом  10 и
10 и 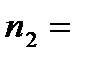 13. По результатам выборок найдены
13. По результатам выборок найдены  82,7 мм,
82,7 мм,  82,3 мм,
82,3 мм,  0,8 и
0,8 и  1,1. В предположении о нормальном законе распределения погрешностей изготовления требуется на уровне значимости
1,1. В предположении о нормальном законе распределения погрешностей изготовления требуется на уровне значимости  0,01 проверить гипотезу
0,01 проверить гипотезу 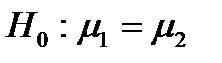 при конкурирующей гипотезе: а)
при конкурирующей гипотезе: а) 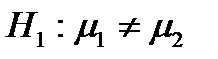 ; б)
; б)  .
.
9.13. Для сравнения точности двух станков-автоматов взяты две выборки объемом  10 и
10 и 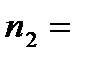 9. По результатам измерения контролируемого размера вычислены выборочные дисперсии
9. По результатам измерения контролируемого размера вычислены выборочные дисперсии  0,95,
0,95,  2,75 и
2,75 и  64,3 мм,
64,3 мм,  64,8 мм. На уровне значимости 0,01 проверить нулевую гипотезу
64,8 мм. На уровне значимости 0,01 проверить нулевую гипотезу  против конкурирующей гипотезы
против конкурирующей гипотезы  .
.
9.14. По результатам двух независимых выборок объемом  9 и
9 и 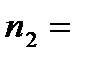 15, извлеченных из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии
15, извлеченных из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии  24,1 и
24,1 и 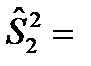 8,6, а также
8,6, а также  46,9 мм и
46,9 мм и  47,2 мм. Проверить на уровне значимости 0,05 нулевую гипотезу о равенстве дисперсий генеральных совокупностей, т.е.
47,2 мм. Проверить на уровне значимости 0,05 нулевую гипотезу о равенстве дисперсий генеральных совокупностей, т.е.  при конкурирующей гипотезе
при конкурирующей гипотезе  .
.
9.15. По четырем независимым выборкам объемом  11,
11, 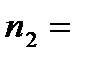 15,
15,  16 и
16 и  20, извлеченным из нормальных генеральных совокупностей, найдены выборочные дисперсии, равные соответственно 3,5; 2,5; 4,0; 5,5. Проверить на уровне значимости 0,02 гипотезу об однородности дисперсий
20, извлеченным из нормальных генеральных совокупностей, найдены выборочные дисперсии, равные соответственно 3,5; 2,5; 4,0; 5,5. Проверить на уровне значимости 0,02 гипотезу об однородности дисперсий  .
.
9.16. Сравнивают точность обработки деталей на четырех станках. Наибольшую точность имеет тот станок, дисперсия контролируемого параметра которого меньше. На первом станке обработано 8 деталей, на втором - 12, на третьем и четвертом по 16 деталей. Исправленные выборочные дисперсии  соответственно равны: 0,0051; 0,0038; 0,0064; 0,0028. Допустив, что ошибки изготовления распределены нормально, на уровне значимости 0,025 проверить гипотезу о том, что все станки имеют одинаковую точность.
соответственно равны: 0,0051; 0,0038; 0,0064; 0,0028. Допустив, что ошибки изготовления распределены нормально, на уровне значимости 0,025 проверить гипотезу о том, что все станки имеют одинаковую точность.
9.17. Три фасовочных автомата настроены на взвешивание одного и того же веса. С целью проверки точностных характеристик автоматов из их продукции взяты выборки объемом  14;
14; 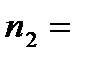 16;
16;  20. Контрольные взвешивания на эталонных весах показали, что величина отклонения веса продукции от заданной величины составила (в граммах).
20. Контрольные взвешивания на эталонных весах показали, что величина отклонения веса продукции от заданной величины составила (в граммах).
| На первом автомате | ||||
Отклонение 
| ||||
Частота 
| ||||
| На втором автомате | ||||
Отклонение 
| ||||
Частота 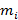
| ||||
| На третьем автомате | ||||
Отклонение 
| ||||
Частота 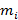
|
Требуется:
а) проверить на уровне значимости 0,1 гипотезу о равенстве точностных характеристик (дисперсий) фасовочных автоматов;
б) найти оценку генеральной дисперсии.
9.18. Пять станков-автоматов выполняют однотипную технологическую операцию. Из продукции каждого станка для контрольных измерений взято по одной выборке из 11 деталей. По результатам выборочных измерений найдены несмещенные оценки дисперсий  : 0,0121; 0,0256; 0,0196; 0,0336; 0,0161. Допустив, что погрешность изготовления есть нормальная случайная величина, проверить при уровне значимости 0,05 гипотезу о том, что точечные характеристики (дисперсии) станков равны.
: 0,0121; 0,0256; 0,0196; 0,0336; 0,0161. Допустив, что погрешность изготовления есть нормальная случайная величина, проверить при уровне значимости 0,05 гипотезу о том, что точечные характеристики (дисперсии) станков равны.
9.19. С целью анализа влияния 4 режимов закалки на прочность деталей каждым режимом закалки обработано по 10 деталей. Исправленные значения выборочных дисперсий, характеризующие вариацию прочности деталей  , равны: 0,26; 0,36; 0,89; 0,47. Требуется на уровне значимости 0,01 проверить гипотезу о равенстве дисперсий, т.е. о независимости вариации прочности деталей от режима закалки.
, равны: 0,26; 0,36; 0,89; 0,47. Требуется на уровне значимости 0,01 проверить гипотезу о равенстве дисперсий, т.е. о независимости вариации прочности деталей от режима закалки.
9.20. Из продукции 4 станков проконтролировано соответственно  150,
150, 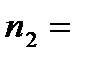 50,
50,  100 и
100 и  175 изделий, из которых оказались дефектными
175 изделий, из которых оказались дефектными 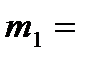 20;
20;  8;
8;  15 и
15 и  30 изделий. На уровне значимости 0,01 и 0,05 проверить гипотезу о том, что вероятности появления дефектного изделия на всех станках равны, т.е.
30 изделий. На уровне значимости 0,01 и 0,05 проверить гипотезу о том, что вероятности появления дефектного изделия на всех станках равны, т.е.  .
.
9.21. Во время экзаменов курсантам были предложены задачи из семи разделов изучаемого курса. Результаты экзамена приведены в таблице.
| Номер раздела курса | |||||||
| Число предложенных для решения задач | |||||||
| Доля решенных задач | 0,855 | 0,509 | 0,522 | 0,484 | 0,860 | 0,412 | 0,420 |
Требуется на уровне значимости 0,1 проверить гипотезу о том, что вероятность решения курсантами задачи не зависит от того, к какому разделу она относится, т.е. 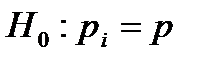 для всех
для всех  .
.
9.22. В механическом цехе завода фланцы крышек обрабатывают на 7 агрегатных станках. Результаты контроля за качеством крышек приведены в таблице.
| Номер станка | |||||||
Число проконтролированных крышек 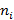
| |||||||
Доля дефектных изделий 
| 0,018 | 0,012 | 0,002 | 0,003 | 0,015 | 0,084 | 0,005 |
Необходимо на уровне значимости 0,001 проверить гипотезу о том, что качество продукции не зависит оттого, на каком станке она изготовлена, т.е. 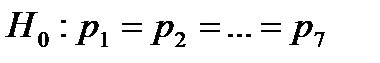 .
.
9.23. Контрольную работу выполнили курсанты шести групп первого курса. Результаты контрольной работы приведены в таблице.
| Шифр группы | ||||||
Число предложенных для решения задач 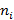
| ||||||
Число правильно решенных задач 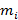
|
Требуется на уровне значимости 0,025 проверить нулевую гипотезу  о том, что не имеется различий в усвоении темы курсантами различных групп потока.
о том, что не имеется различий в усвоении темы курсантами различных групп потока.
9.24. Поставщик ламп накаливания утверждает, что средний срок службы равен 3000 ч. Для выборки из 30 ламп средний срок службы равен 2845 ч при среднем квадратическом отклонении 685 ч. Требуется:
а) проверить справедливость утверждения поставщика при уровне значимости 0,05;
б) при  2900 ч вычислить мощность критерия.
2900 ч вычислить мощность критерия.
9.25. По данным руководителя предприятия он получает заказы от 30% предполагаемых клиентов. Можно ли считать точным его утверждение при уровне значимости 0,1, если предприятие получил заказы от 25 из 100 случайно отобранных потенциальных клиентов.
9.26. Согласно рекламе, применение предполагаемых удобрений повышает урожайность пшеницы не менее, чем на 5 ц/га. Удобрения вносили в почву на 26 га, в результате чего был получен урожай на 4 ц/га выше, чем на контрольном поле, при среднем квадратическом отклонении 2 ц/га. Проверить справедливость утверждения рекламы при уровне значимости 0,01 или 0,05.
9.27. Удобрения двух марок вносили в почву соответственно на 15 и 14 га. На этих полях средняя урожайность пшеницы составила 33,2 и 32,3 ц/га при средних квадратических отклонениях 3 и 4 ц/га. Можно ли при уровне значимости 0,05 отдать предпочтение одной из марок удобрений по их влиянию на урожайность?
9.28. Продюсер телевизионной передачи утверждает, что она привлекла не менее трети телезрителей. Из 168 опрошенных телезрителей каждый четвертый смотрел передачу. Требуется:
а) на 5%-ном уровне значимости проверить справедливость утверждения продюсера;
б) при  0,01 сравнить по популярности эту передачу с другой, которая одновременно с первой шла по одной из программ, но которую смотрело 50 телезрителей из опрошенных.
0,01 сравнить по популярности эту передачу с другой, которая одновременно с первой шла по одной из программ, но которую смотрело 50 телезрителей из опрошенных.
9.29. Средний срок службы 15 подвергнутых испытанию батареек первой фирмы оказался равным 121 ч при среднем квадратическом отклонении 2 ч. По данным испытаний 10 батареек второй фирмы средний срок службы равен 118 ч. при  3 ч. Требуется сравнить качество батареек этих фирм по сроку службы на 5%-ном уровне значимости.
3 ч. Требуется сравнить качество батареек этих фирм по сроку службы на 5%-ном уровне значимости.
9.30. Средний дневной объем продаж для 15 торговых точек одного района составляет 3,6 млн. руб. при среднем квадратическом отклонении 0,6 млн. руб., а 10 торговых точек другого района характеризуется соответственно значениями 3,4 млн. руб. и 0,5 млн. руб. Требуется:
а) сравнить объемы продаж в этих районах на 5%-ном уровне значимости;
б) проверить значимо ли превышение объема продаж в первом районе по сравнению со вторым при  0,1;
0,1;
в) определить в чем различие вопросов а) и б).
9.31. В таблице указано число телезрителей (мужчин и женщин), проявивших положительное, безразличное и отрицательное отношение к рекламной телевизионной передаче.
| Отношение к рекламе | Пол | |
| Мужчины | Женщины | |
| Положительное | ||
| Безразличное | ||
| Отрицательное |
Требуется при уровне значимости 0,01 сравнить телезрителей по их отношению к рекламе с учетом пола.
9.32. В целях изучения изменений в потребительском спросе автомобильная фирма провела опрос вошедших в случайную выборку 50 мужчин и 50 женщин, которые в предыдущем году купили автомобили этой фирмы. В таблице приведены ответы опрошенных относительно установки наиболее важных дополнительных устройств, Обеспечивающих повышение безопасности.
| Покупатели | Дополнительные устройства | |||
| Дисковые тормоза | Складывающееся рулевое колесо | Автоматические дверные замки | Сигнал превышения скорости | |
| Мужчины | ||||
| Женщины |
Проверить при  0,05 имеются ли существенные расхождения во взглядах мужчин и женщин - владельцев автомобилей на дополнительные устройства.
0,05 имеются ли существенные расхождения во взглядах мужчин и женщин - владельцев автомобилей на дополнительные устройства.
9.33. Фирма, выпускающая прибор, провела маркетинговое исследование, опросив 100 покупателей. Полученные данные о месте покупки изделия и источнике сведений о нем приведены в таблице:
| Источник сведений | Место покупки | ||
| Универмаг | Магазин с низкими ценами | Специализированный магазин | |
| Друзья | |||
| Газеты | |||
| Журналы |
Руководство фирмы предполагает, что сбыт прибора одинаков через магазины всех трех типов. Проверьте это предположение на 5%-ном уровне значимости.
9.34. В рекламе фирмы утверждается, что картофель, выращенный по голландской технологии, дает урожайность не ниже 43 ц/га. По этой технологии картофель вырастили на площади 23 га, получив при этом урожай в среднем 42 ц/га при среднем квадратическом отклонении 1,5 ц/га. Необходимо проверить справедливость утверждения рекламы при уровне значимости 0,05.
9.35. Из продукции трех швейных цехов проконтролировано соответственно 125, 40 и 78 изделий, из которых оказались дефектными соответственно 10, 4 и 7 швейных изделий. Требуется на 5%-ном уровне значимости сравнить вероятности появления дефектного изделия в этих цехах.
9.36. Требуется сравнить при  0,05 производительность труда в строительных организациях, имеющих организационно-правовые формы в виде акционерного общества закрытого типа и товарищества с ограниченной ответственностью. Анализ показал, что на 25 предприятиях первого типа средняя производительность труда составила 6,8 млн. руб. на одного работника при
0,05 производительность труда в строительных организациях, имеющих организационно-правовые формы в виде акционерного общества закрытого типа и товарищества с ограниченной ответственностью. Анализ показал, что на 25 предприятиях первого типа средняя производительность труда составила 6,8 млн. руб. на одного работника при  0,6 млн. руб., а на 13 предприятиях второго типа 6,2 млн. руб. при
0,6 млн. руб., а на 13 предприятиях второго типа 6,2 млн. руб. при  0,8 млн. руб.
0,8 млн. руб.
9.37. Независимые эксперты утверждают, что не менее 1/3 безработных не обращаются в службу занятости, а находят работу самостоятельно с помощью рекламы. Из 208 опрошенных безработных каждый четвертый действительно не обращался в службу занятости. Требуется при 2%-ном уровне значимости:
а) проверить справедливость утверждения экспертов;
б) сравнить долю безработных, не обращающихся в службу занятости, и долю безработных, нашедших работу на основании рекламы, если число последних среди опрошенных равно 40.
9.38. По данным рекламы использование новой БИС (большой интегральной схемы) позволяет повысить быстродействие компьютера на 16 тыс.оп/с при  1 тыс.оп./с. Проверить на 1%-ном уровне значимости добросовестность рекламы.
1 тыс.оп./с. Проверить на 1%-ном уровне значимости добросовестность рекламы.
9.39. Утверждается, что применение рекламируемого препарата пищевой добавки, разрушающей жировой слой, позволяет снизить вес за 1 месяц его применения в среднем на 7 кг. В результате обследования 27 человек, употребляющих данный препарат, установлено, что они похудели в среднем на 6 кг при  1,5 кг. Требуется проверить при
1,5 кг. Требуется проверить при  0,05 добросовестность рекламы.
0,05 добросовестность рекламы.
9.40. Сторонники строительства крупной ГЭС утверждают, что более половины населения области поддерживают данное строительство. Из 345 опрошенных жителей 42$ высказались за данный проект, а 25% - за строительство малых ГЭС. Требуется при 5%~ном уровне значимости:
а) проверить справедливость утверждения сторонников крупной ГЭС;
б) сравнить количество сторонников крупной и малых ГЭС.
9.41. При проверке дальномера произведено 200 измерений базы, равной 3000 м.отклонения результатов измерений от истинного значения измеряемой величины представлены в таблице.
| № разряда | |||||
| Граница интервала | -20…-15 | -15…-10 | -10…-5 | -5…0 | 0…5 |
| mi | |||||
| № разряда | |||||
| Граница интервала | 5…10 | 10…15 | 15…20 | 20…25 | 25…30 |
| mi |
Оценить с помощью критерия χ2 гипотенузу о согласии выборочного распределения с законом нормального распределения при уровне значимости  =0,05.
=0,05.
9.42. Произведено 500 измерений ошибок наводки при стрельбе по движущим целям. Результаты измерений в делениях угломера представлены статистическим рядом.
| Границы интервала | -4…-3 | -3…-2 | -2…-1 | -1…0 |
| mj | ||||
| Рj | 0,012 | 0,050 | 0,144 | 0,266 |
| Границы интервала | 0…1 | 1…2 | 2…3 | 3…4 |
| mj | ||||
| Рj | 0,240 | 0,176 | 0,092 | 0,020 |
Проверить гипотезу с нормальном распределении ошибок наводки, используя критерий χ2.
9.43. С целью исследования закона распределения ошибок измерений дальности дальномером ДС-20 произведено 400 измерений дальности. Результаты измерений представлены в таблице
| Границы интервала | 20…30 | 30…40 | 40…50 | 50…60 |
| mj | ||||
| Рj | 0,052 | 0,180 | 0.165 | 0,095 |
| Границы интервала | 60…70 | 70…80 | 80…90 | 90…100 |
| mj | ||||
| Рj | 0,128 | 0,140 | 0,160 | 0,080 |
Используя критерий χ2,проверить гипотенузу о равномерном распределении ошибок измерения дальности дальномером ДС-2.
9.44. Результаты измерений массы 1000 снарядов калибра 203,2мм представлены в таблице.

| 98,0 | 98,5 | 99,0 | 99,5 | 100,0 |
| mj | |||||
| Рj | 0,021 | 0,047 | 0,087 | 0,158 | 0,181 |

| 100,5 | 101,0 | 101,5 | 102,0 | 102,5 |
| mj | |||||
| Рj | 0,201 | 0,142 | 0,097 | 0,021 | 0,025 |
Пользуясь критериями согласия Колмогорова, проверить согласие полученных результатов с предположением о нормальном распределении массы снарядов. Уровень значимости  принять равным 0,05.
принять равным 0,05.
9.45. В таблице представлены результаты проверки датчика случайных чисел.
| Интервалы | 0…0,1 | 0,1…0,2 | 0,2…0,3 | 0,3…0,4 | 0,4…0,5 |
| mj | |||||
| Интервалы | 0,5…0,6 | 0,6…0,7 | 0,7…0,8 | 0,8…0,9 | 0,9…0,10 |
| mj |
Проверить с помощью критерия согласия Колмогорова гипотезу о равномерном распределении случайной величины X-числа выдаваемого датчиком случайных чисел.
9.46. Величины отклонений точек падения 250 снарядов от центра рассеивания приведены в таблице.
| Границы интервала | 0…3 | 3…6 | 6…9 | 9…12 | 12…15 | 15…18 | 18…21 | 21…24 |
| mj | 0,5 | 1,5 | 17,5 | 28,5 | ||||
| Границы интервала | 24…27 | 27…30 | 30…33 | 33…38 | 38…39 | 39…42 | 42…45 | 45…48 |
| mj | 30,5 | 27,0 | 7,5 | 1,0 | 1,0 |
Используя критерии согласия χ2 и Колмогорова, установить, согласуется ли опытный материал с законом нормального распределения, за параметры которого принять оценки математического ожидания и среднего квадратического отклонения.
9.47. При измерен дальности дальномером в ДС-1 получены результаты: 1965, 1930, 2090, 1945 м. Оценить, не является ли результат 2090 анормальным?
9.48. При определении начальной скорости снаряда с помощью 5 артиллерийских баллистических станций получены результаты: 284,6; 287,2; 283,4; 286,4; 294,8 м/с. Определить, следует ли включать в обработку результат 294 м/с?
9.49. Производился замер длины зарядной каморы орудия прибором ПЗК. Получены результаты: 291,6; 292,4; 291,2; 293,8. Следует ли учитывать результат 293,8?
9.50. Стреляющая минометная батарея противника засекалась радиолокационной станцией. Получены следующие дальности 6168; 6150; 6190; 6160; 6270 м. Следует ли включать в обработку результат 6270 м?
9.51. Стандартная масса таблетки – 0,5 мг. Возникло подозрение, что она больше. Была проверена партия из 121 таблетки с целью проверки гипотезы при уровне значимости a=0,01, если известно, что σх=0,11 мг. Подтвердилось ли подозрение?
9.52. По выборке объема n=9 при известном σх= и уровне значимости a=0,05 проверить гипотезу Но: mx= 15 при альтернативе Н1: rx>15 (mx=17).
9.53. По выборке объема n=16 при известном σх=5 и уровне значимости a=0,05 проверить гипотезу Но: mx= 20 при альтернативе Н1:  Найти
Найти  .
.
9.54. Двумя методами проведены измерения одной и той же величины. При этом получены следующие результаты: I – 9,6; 10,0; 9,8; 10,2; 10,6. II – 10,4; 9,7; 10,0; 10,3. Можно ли считать, что оба метода обеспечивают одинаковую точность при уровне значимости a=0,01?
9.55. По двум независимым выборкам из нормальных совокупностей, объемы которых n1=9; n2=6, найдены 
 . Проверить нулевую гипотезу Но:
. Проверить нулевую гипотезу Но:  при альтернативе Н1:
при альтернативе Н1: 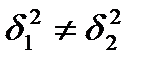 .
.
9.56. На двух стендах получены данные по оценке предела прочности на разрыв. Можно ли считать, что оба стенда одинаково точно позволяют определить предел прочности на разрыв?
| Стенд 1 | 1,324 | 1,322 | 1,327 | 1,342 | 1,301 | 1,309 | 1,174 | 1,319 | 1,392 | 1,396 |
| Стенд 2 | 1,358 | 1,318 | 1,318 | 1,321 | 1,414 | 1,398 | 1,375 | 1,347 | 1,366 | 1,408 |
9.57. Проверяется отсутствие разладки работы станка по величине контролируемого изделия. Взяли 15 проб по 20 изделий в каждой, после чего вычислялись несмещенные оценки дисперсий, которые представлены в таблице:
| 0,082 | 0,109 | 0,112 |
| 0,094 | 0,121 | 0,109 |
| 0,162 | 0,094 | 0,110 |
| 0,143 | 0,156 | 0,156 |
| 0,121 | 0,110 | 0,164 |
Можно ли при уровне значимости a считать, что разладка не произошла?
9.58. Каждая из трех лаборатории произвела анализ 10 проб сплава для определения процентного содержания углерода, причем несмещенные оценки дисперсий оказались равными 0,045; 0,062; 0,093. Проверить при уровне значимости a=0,01 гипотезу об однородности дисперсий.
9.59. Проверка скорости полимеризации проводится на нескольких образцах. Предполагаемая скорость полимеризации составляет 24 % в час. В восьми опытах были получены следующие результаты: 23,6; 22,6; 24,8; 26,4; 24,3; 23,9; 25,0% в час. Есть ли основания для того, чтобы считать полученные результаты не совместны с предполагаемым значением средней скорости?
9.60. Исследовались образцы, у которых обработка поверхности проводилась двумя разными методами. Требуется решить при уровне значимости a = 0,05, могут ли представленные ниже данные принадлежать одной нормальной совокупности?
| Первый способ | ||||||||||
| Второй способ |
9.61. По выборке n = 50 найдено  = 20,1мм – средний размер диаметра валика, а по второй выборке n2 = 50 средний размер диаметра
= 20,1мм – средний размер диаметра валика, а по второй выборке n2 = 50 средний размер диаметра 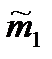 =19,8мм. Точность в первой выборке оценивалась дисперсией
=19,8мм. Точность в первой выборке оценивалась дисперсией 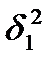 = 1,750мм2,а во второй выборке
= 1,750мм2,а во второй выборке  = 1,375. Проверить при уровне значимости a = 0,05 гипотезу Ḥ0: m1 = m2 при альтернативе Ḥ1: m 1≠ m2.
= 1,375. Проверить при уровне значимости a = 0,05 гипотезу Ḥ0: m1 = m2 при альтернативе Ḥ1: m 1≠ m2.
9.62. Для разработки нормативов проанализируем данные потребления электроэнергии по 8 объектам в условных единицах: 5,22; 5,23; 5,24; 5,26; 5,29; 6,30; 6,43. Два последних наблюдения кажутся аномальными. Проверить с помощью критерия при уровне значимости a = 0,01. Так ли это на самом деле?
9.63. Измеряется сопротивление проволоки. При исследовании 8 образцов были получены следующие результаты: 0,129; 0,132; 0,136; 0.139; 0,132; 0,137; 0,125; 0,136. Если основания для того, чтобы исключить из выборки какое - либо значение?
9.64. При уровне значимости a = 0,05проверить гипотезу о согласии эмпирического распределения с показательным законом.
| (xi1 xi+1) | 0-1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 |
| mi |
9.65. В библиотеке случайно отобрано 200 выборок по 5 книг. Регистрировалось число поврежденных книг. В итоге получено эмпирическое распределение числа xṫ поврежденных книг в одной