Основные понятия дискриминантного анализа. Задачи, решаемые с помощью дискриминантного анализа.
Дискриминантный анализ применяется для решения 2 задач – 1) описания различия между классами и 2) классификации объектов, не входивших в первоначальную обучающую выборку.
Для решения 1й задачи строится множество дискриминантных функций, которые позволяют с максимальной эффективностью «разделить» классы. Для того, чтобы выделить p классов, требуется не более p-1 канонической дискриминантной функции.
Для решения 2й задачи – рассчитываются расстояния от каждого нового объекта до центра тяжести кластеров. Могут учитываться априорные вероятности принадлежности к кластерам и цена ошибок классификации.
Основные идеи вероятностных методов классификации.
Задача Отнесения n-наблюдений Xi, где i=1,2,..,n к одному из p-классов.
Под классом понимается генеральная совокупность, описываемая одномодальной функцией плотности f(x)
(или одномодальным полигоном вероятностей в случае дискретных признаков X).
Идея вероятностных методов классификации:
Наблюдение xi будет относится к тому классу (той генеральной совокупности) в рамках которой оно выглядит более правдоподобно.
Принцип может корректироваться с учетом удельных весов классов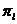 
и особенности «функции потерь» C(l/m), которая определяет стоимость потерь от ошибочного отнесения объекта m-го класса к классу с номером l (l,m=1,2,…,p)
Дискриминантный анализ, функции потерь и вероятности неправильной классификации.
Методы классификации следует выбирать по условию минимизации потерь или вероятности неправильной классификации объектов.
Исследуем связь этих двух характеристик качества метода классификации
Обозначим C(l/m) – потери, связанные с ошибочным отнесением объекта m-го класса к классу l. (при l=m, очевидно C(l/m) =0.
Пусть в процессе классификации таких ошибок было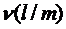 
. Тогда потери, связанные с ошибочным отнесением объектов m-го класса к классу l составляют 
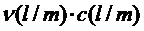по всем l,m=1,2,…,р. Общие потери Сn при такой процедуре классификации составят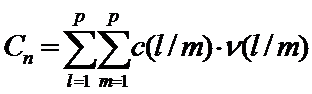 
Тогда удельная характеристика потерь при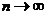 
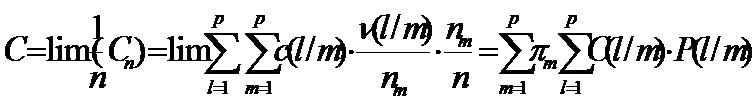
Здесь предел понимается в смысле сходимости по вероятности относительных частот
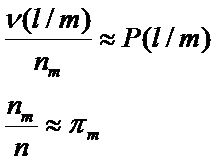где P(l/m) – вероятность отнести объект класса m к классу l
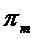- вероятность извлечения объекта класса m из общей совокупности объектов.
Величину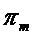 
называют априорной вероятностью (удельным весом) класса m.
Средние потери от неправильной классификации объектов m-го класса равны:
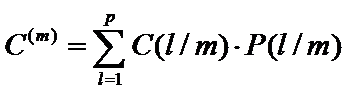
Средние удельные потери от неправильной классификации всех анализируемых объектов составят:
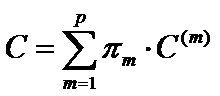
Обычно предполагают, что потери C(l/m) одинаковы для любой пары l и m, то есть
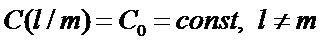
Тогда минимизация средних удельных потерь С будет эквивалентна максимизации вероятности правильной классификации объектов
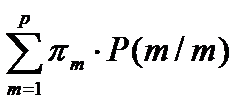
Тогда
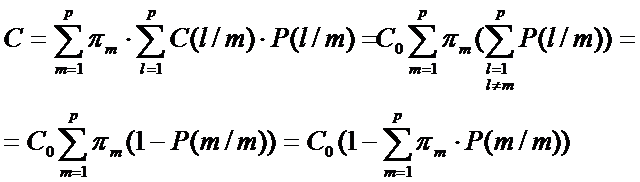
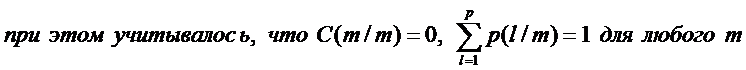
В этом случае при построении процедур классификации часто говорят не о потерях, а о вероятности неправильной классификации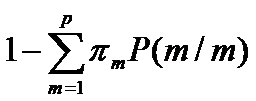 
Построение оптимальных (байесовских) процедур классификации.
Пусть требуется классифицировать n k-мерных наблюдений x1,x2,…,xn при наличии обучающих выборок типа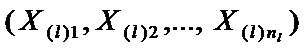 
, где l=1,2,…,p и x(l)i – есть i наблюдение в l-й выборке.
Каждая выборка определяет значения анализируемых признаков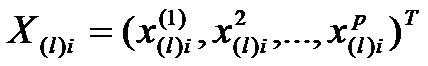 
на nl объектах (где i=1,2,…,nl).
Априорно известно, что все nl наблюдения принадлежат l-му классу и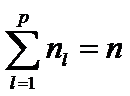 
Классифицируемые n наблюдений в данной задаче интерпретируются как выборка из генеральной совокупности, описываемой смесью р-одномерных генеральных совокупностей с плотностью вероятности
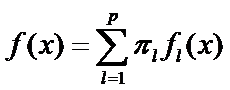где 
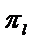- априорная вероятность появления в выборке элемента l – го класса с плотностью 
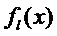или удельный вес элементов l – го класса в общей генеральной совокупности.
Введем понятие решающего правила дискриминантной функции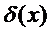 
, которая может принимать только целые положительные значения 1,2,…,р. Причем все наблюдения X, для которых она принимает значение l, будем относить к l-му классу, т.е.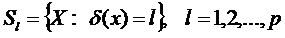 
Очевидно, что S(l) – это k-мерные подобласти в пространстве возможных значений признака X. Функция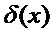 
строится таким образом, чтобы подобласти S1,S2,…,Sp были взаимно не пересекающимися и охватывали все n наблюдений.
Таким образом, решающее правило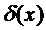 
может быть задано разбиением S= (S1,S2,…,Sp) всего р-мерного пространства, включающего n наблюдений на p - непересекающихся областей.
Решающее правило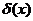 
называется оптимальным байесовским, если оно сопровождается минимальными потерями С среди других процедур классификации. Оптимальная процедура классификации 
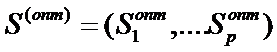определяется следующим образом:
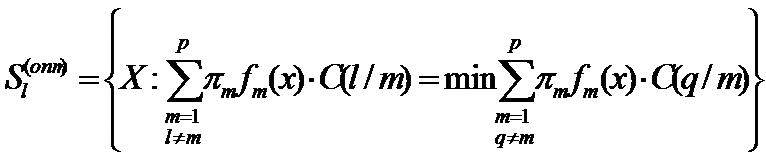Таким образом, наблюдение 
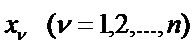будет отнесено к классу 
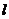тогда, когда средние удельные потери от его отнесения именно к этому классу окажутся минимальными по сравнению с потерями от его отнесения к любому другому классу.
Решающее правило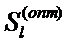 
значительно упростится в случае, когда потери равны, т.е. 
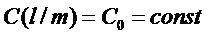.В этом случае наблюдение 
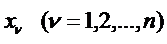будет отнесено к классу l тогда, когда 
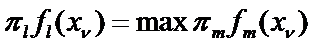То есть максимизируется взвешенная «правдоподобность» наблюдения 
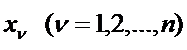в рамках класса, где в к качестве весов выступают априорные вероятности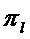 
Чтобы теоретические оптимальные правила можно было бы построить, необходимо иметь оценки априорных вероятностей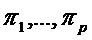 
и плотностей 
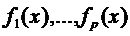. Эти оценки в статистическом варианте решения задачи получаются на основе обучающих выборок. Оценки априорных вероятностей имеют вид 
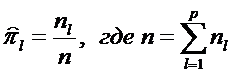- объем суммарной выборки
5. Параметрический дискриминантный анализ в случае нормального распределения внутри классов. Число классов p=2.
Пусть l-й класс описывается k-мерным нормальным законом распределения с вектором математических ожиданий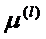 
и ковариационной матрицей 
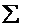(общей для всех p-классов 
).
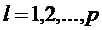Оценки параметров распределения находятся по обучающим выборкам объемом nl:
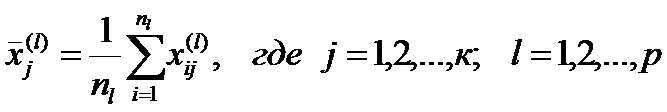, где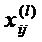 
- значение j–го показателя для i-го наблюдения l–й выборки.
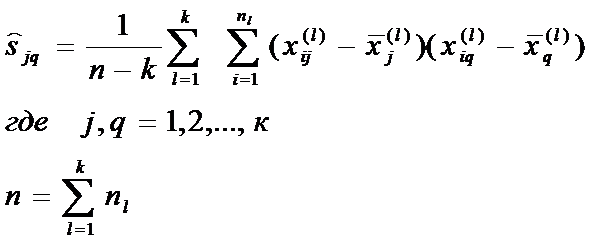
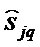- оценка коэффициента ковариации между xj и xq - ми переменными, полученная по суммарной выборке объемом n.
Тогда оценка плотности распределения l-й совокупности имеет вид:
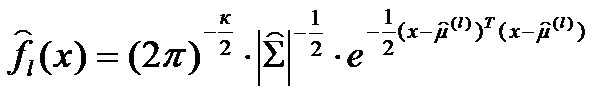
где
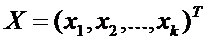- вектор-столбец текущих переменных
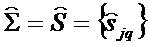- несмещенная оценка ковариационной матрицы
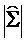- определитель ковариационной матрицы
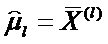- вектор средних значений переменных для l-й обучающей выборки.
Правило классификации:
Наблюдение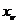 
относится к классу l0 тогда и только тогда
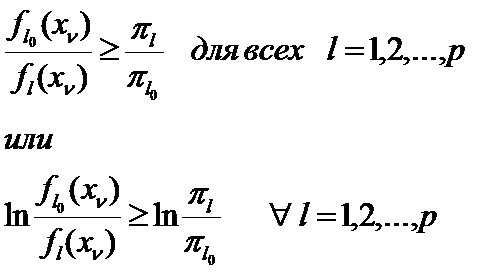
Рассмотрим случай: p=2, X и Y – генеральные совокупности. Выборочное пространство, множество возможных реализаций W случайных величин X и Y можно разделить на две области гиперплоскостью
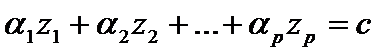,где 
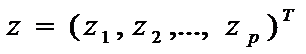- значения показателей наблюдения, подлежащего дискриминации. Левая часть уравнения 
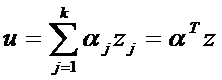называется дискриминантной функцией, позволяющей перейти от к-мерного пространства к одномерному, где 
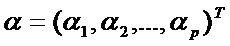- вектор коэффициентов дискриминантной функции.
Таким образом, две области пространства можно задать неравенствами:
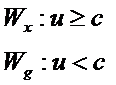
Если имеется элемент выборки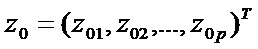 
, то его относим к X, при 
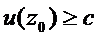и к Y при 
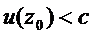Таким образом, задача дискриминации сводится к определению коэффициентов дискриминантной функции 
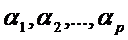и константы с.
Предположим, что известны априорные вероятности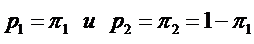 
и наблюдаемый объект принадлежит к первой X или второй Y генеральной совокупности. Также известны ущербы от ошибочной классификации:
С(Y/X) – ошибочного отнесения вектора наблюдения Z0, принадлежащего первой совокупности (X), ко второй (Y), а также C(X/Y) – потери от ошибочного отнесения Z0 к X вместо Y. Предполагается также, что неизвестны параметры генеральной совокупности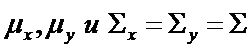 
При таких условиях задача дискриминации решается с помощью, так называемой, обобщенной байесовской процедуры классификации.
Сначала по обучающим выборкам n1 и n2 найдем оценки параметров генеральных совокупностей X и Y, вектора средних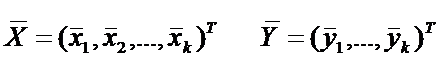 
и оценку ковариационной матрицы 
;
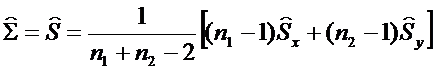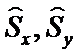- несмещенные оценки ковариационных матриц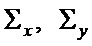 
Тогда вектор оценок коэффициентов дискриминантной функции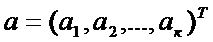 
можно получить по формуле 
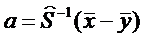. А оценка дискриминантной функции 
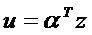равна 
Воспользовавшись оценкой дискриминантной функции получим n1 значение этой функции для первой выборки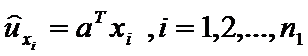 
и среднее значение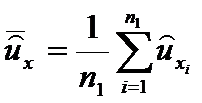 
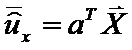
Аналогично найдем для второй выборки из Y
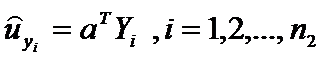и 
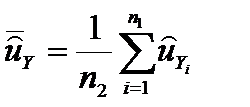
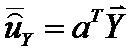
Константа оценивается выражением
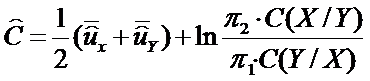если принять, что
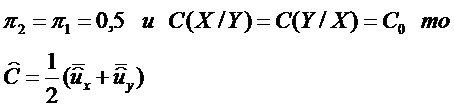
Тогда, если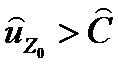 
, то Z0 относится к X, а если 
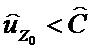, то Z0 относится к Y.
6. Параметрический дискриминантный анализ в случае нормального распределения внутри классов. Число классов p>2.
Пусть l-й класс описывается k-мерным нормальным законом распределения с вектором математических ожиданий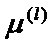 
и ковариационной матрицей 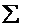(общей для всех p-классов 
).
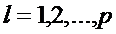Оценки параметров распределения находятся по обучающим выборкам объемом nl:
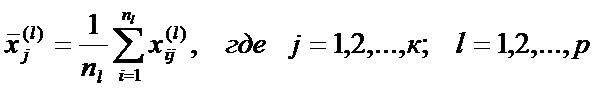, где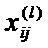 
- значение j–го показателя для i-го наблюдения l–й выборки.
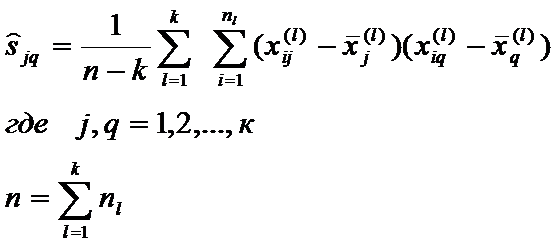
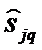- оценка коэффициента ковариации между xj и xq - ми переменными, полученная по суммарной выборке объемом n.
Тогда оценка плотности распределения l-й совокупности имеет вид:
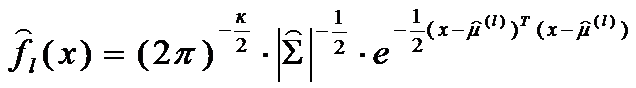
где
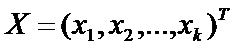- вектор-столбец текущих переменных
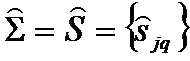- несмещенная оценка ковариационной матрицы
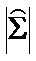- определитель ковариационной матрицы
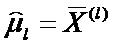- вектор средних значений переменных для l-й обучающей выборки.
Правило классификации:
Наблюдение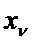 
относится к классу l0 тогда и только тогда
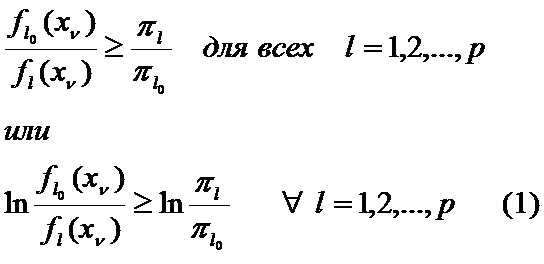
Рассмотри процедуру дискриминации для случая р>2 нормально распределенных генеральных совокупностей Xl с параметрами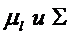 
, где l=1,2,…,p.
Оценку плотности fl(x) совокупности Xl можно представить как:
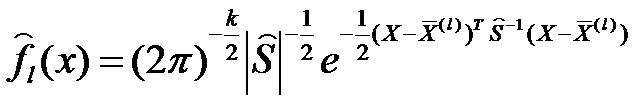
где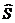 
– несмещенная оценка ковариационной матрицы 
, полученная по р - выборкам
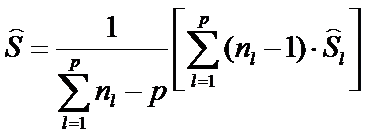
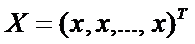- вектор-столбец текущих переменных;
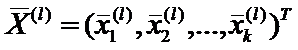- вектор средних значений, полученных по l-ой обучающей выборке
Предположив, что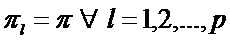 
логарифм отношения правдоподобия (1) можно представить в виде
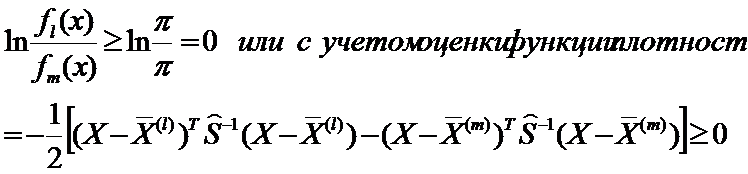
Преобразуем левую часть неравенства, получим:
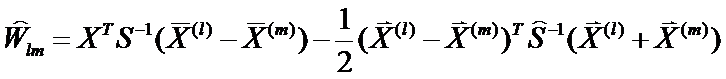
Правило дискриминации: если для всех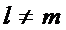 
, где m=1,2,…,k выполняется неравенство 
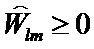, то наблюдение X относится к Xl.
Приведенное правило эквивалентно критерию:
Наблюдение, определяемое вектором X, следует отнести к той совокупности Xl, расстояние Махаланобиса до центра которой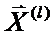 
минимально
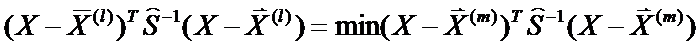а, следовательно, согласно оценки функции плотности апостериорная плотность максимальна.