Призма, у которой боковые ребра перпендикулярны основаниям, а основания – равные квадраты.
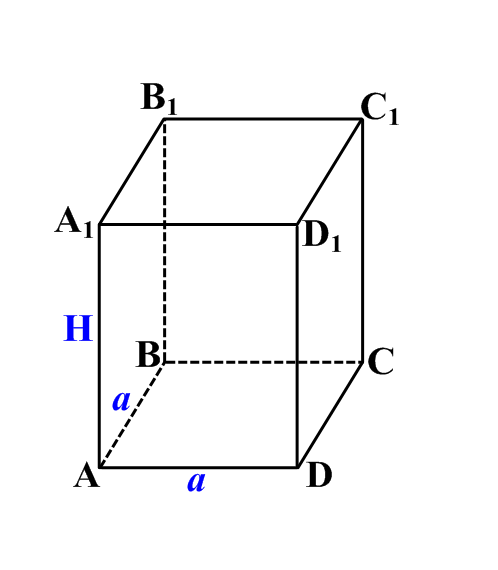
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| V = SоснH | S = 4aH | S = a2 | S = Sбок+2Sосн |
| V = a2H | S = 4 aH + a2 |
1. Боковые грани – равные прямоугольники
2. Сторона основания 
Задачи
1. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 5.
Ответ: 62.
2. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Ответ: 10.
3. Найдите боковое ребро правильной четырехугольной призмы, если стороны ее основания равны 3, а площадь поверхности равна 66.
Ответ: 4.
4. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 2. Найдите площадь боковой поверхности призмы.
Ответ: 32.
5. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Ответ: 3.
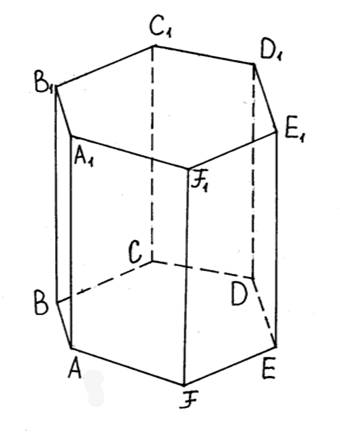
Прямая призма (шестиугольная правильная)
Призма, у которой боковые ребра перпендикулярны основаниям, а основания – равные квадраты.
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| V=SоснH | S = 6aH | 
| S= Sбок+2Sосн |
| 
| 
|
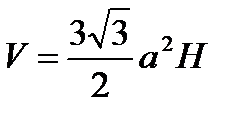
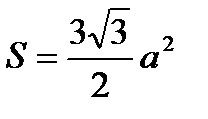
1. Боковые грани – равные прямоугольники
2. Сторона основания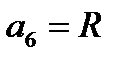 
Задачи
1. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны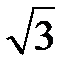 
.
Ответ: 4,5.
2. Найдите площадь боковой поверхности правильной шестиугольной призмы, стороны основания которой равны 3, а высота равна 6.
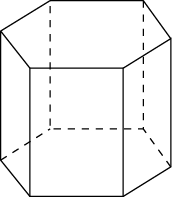
Ответ: 108.
3. Найдите объем правильной шестиугольной призмы, все ребра которой равны √3.
Ответ: 13.5
4. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
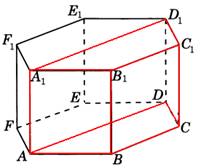
Ответ: 6
Прямая призма (произвольная n -угольная)
Призма, у которой боковые ребра перпендикулярны основаниям, а основания – равные n-угольники.
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| V = SоснH | Если основанием является правильный многоугольник, то S = n aH |
| S = Sбок+2Sосн |
Если основанием является правильный многоугольник, то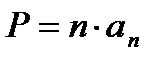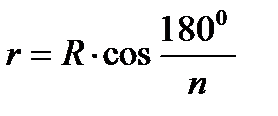  
|
1. Если основанием является правильный многоугольник, то боковые грани – равные прямоугольники.
2. Сторона основания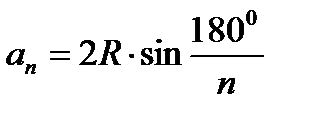 
.
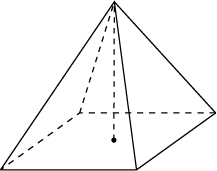
Пирамида
Пирамида –многогранник, составленный из n-угольника A1A2...AnA1 и n треугольников (A1A2P, A1A3P и т.д.).
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| 
|
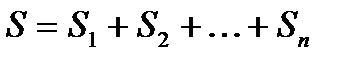
| S = Sбок + Sосн |
| Если основанием является правильный многоугольник, то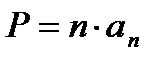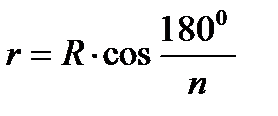
|
1. Сечение, параллельное основанию пирамиды, представляет собой многоугольник, подобный основанию. Площади сечения и основания относятся как квадраты их расстояний до вершины пирамиды.
2. Пирамида называется правильной, если её основание – правильный многоугольник, а вершина проецируется в центр основания.
3. Все боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
4. Высота боковой грани правильной пирамиды называется апофемой.
5. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Задачи
1. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
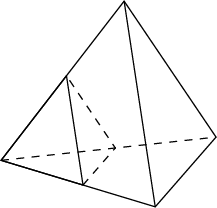Ответ: 8.
2. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды.
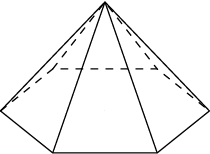Ответ: 360.
5. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.
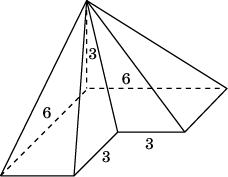Ответ: 27.
6. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна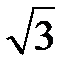 
.
Ответ: 0,25.
7. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
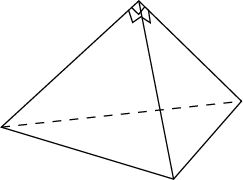Ответ: 4,5.
8. Диагональ основания правильной четырехугольной пирамиды равна 8. Боковое ребро равно 5. Найдите объем пирамиды.
Ответ: 32.
9. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро пирамиды.
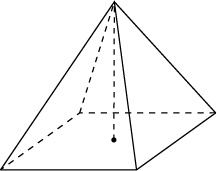Ответ: 13.
10. Стороны основания правильной четырехугольной пирамиды равны 6, боковые ребра равны 5. Найдите площадь поверхности пирамиды.
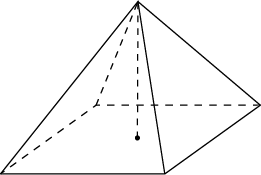Ответ: 84.
11. Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
Ответ: 7.
12. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
Ответ: 4.
13. Объем правильной четырехугольной пирамиды равен 12. Найдите объем пирамиды, отсекаемой от нее плоскостью, проходящей через диагональ основания и середину противоположного бокового ребра.
Ответ: 3.
14. Во сколько раз уменьшится объем октаэдра, если все его ребра уменьшить в два раза?
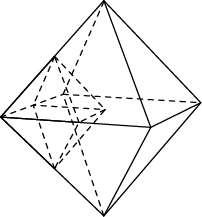Ответ: 8.
15. Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1: 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
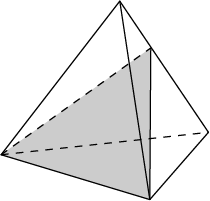Ответ: 10.
16. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен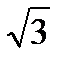 
.
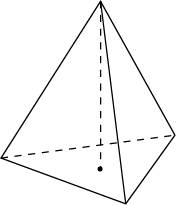Ответ: 3.
17. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Ответ: 256.
18. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Ответ: 3.
Цилиндр
Цилиндр - тело, ограниченное цилиндрической поверхностью и двумя кругами с границами.
| H |
| R |
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| 
| 
| 
|
| 
| 
|
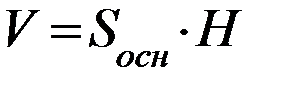
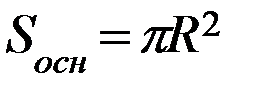
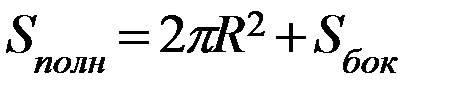
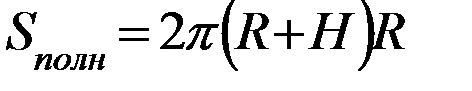
1. Образующие цилиндра - отрезки образующих, заключенные между основаниями.
2. Высота цилиндра - длина образующей.
3. Осевое сечение – прямоугольник, две стороны которого образующие, а две другие - диаметры оснований цилиндра.
4. Круговое сечение – сечение, секущая плоскость которого перпендикулярна к оси цилиндра.
5. Развертка боковой поверхности цилиндра - прямоугольник, представляющий собой два края разреза боковой поверхности цилиндра по образующей.
6. Площадь боковой поверхности цилиндра - площадь ее развертки.
7. Площадь полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
8. Около цилиндра всегда можно описать шар. Его центр лежит на середине высоты.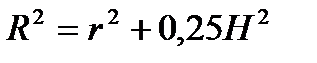 
, где R – радиус шара, r – радиус основания цилиндра, H – высота цилиндра.
9. В цилиндр можно вписать шар, если диаметр основания цилиндра равен его высоте,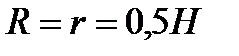 
.
Задачи
1. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?
Ответ: 3.
2. Найдите объем цилиндра, площадь основания которого равна 1, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
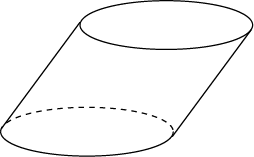Ответ: 3.
3. Цилиндр и конус имеют общие основание и высоту. Найдите объем цилиндра, если объем конуса равен 50.
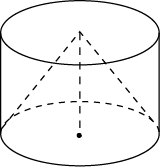Ответ: 150.
4. Воду, находящуюся в цилиндрическом сосуде на уровне 12 см, перелили в цилиндрический сосуд, в два раза большего диаметра. На какой высоте будет находиться уровень воды во втором сосуде?
Ответ: 3.
5. Площадь осевого сечения цилиндра равна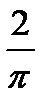 
. Найдите площадь боковой поверхности цилиндра.
Ответ: 2.
6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 2. Найдите площадь боковой поверхности призмы.
Ответ: 32.
7. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Ответ: 2.
8. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
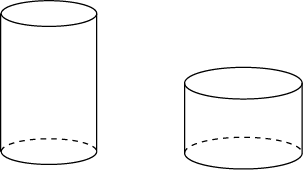Ответ: 1,125.
9. В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого?
Ответ: 2.
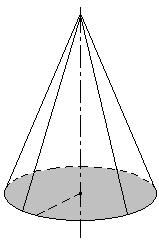
Конус
Конус - тело, ограниченное конической поверхностью и кругом.
 
|
| ось конуса |
| Р |
| вершина |
| образующие |
| боковая поверхность |
| r |
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| 
|
| 
|
| 
|
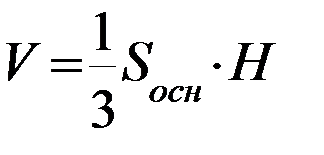
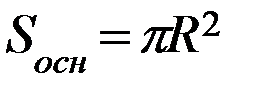
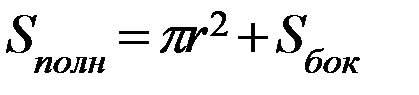
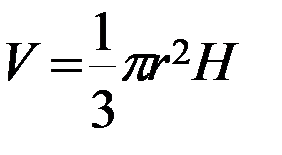
1. Площадь боковой поверхности конуса – площадь ее развертки.
2. Связь между углом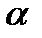 
развертки и углом 
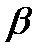при вершине осевого сечения 
.
1. Цилиндр и конус имеют общие основание и высоту. Найдите объем цилиндра, если объем конуса равен 50.
Ответ: 150.
2. Найдите объем конуса, площадь основания которого равна 2, а образующая равна 6 и наклонена к плоскости основания под углом 30о.
Ответ: 2.
3. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.
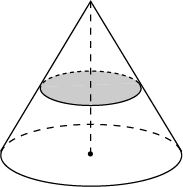Ответ: 1,5.
4. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
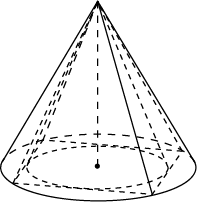Ответ: 2.
5. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на 
.
Ответ: 128.
6. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 48.
Ответ: 16.
7. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на .
Ответ: 9.
8. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на .
Ответ: 16.
9. Конус получается при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 6. Найдите его объем, деленный на .
Ответ: 72.
Сфера и шар
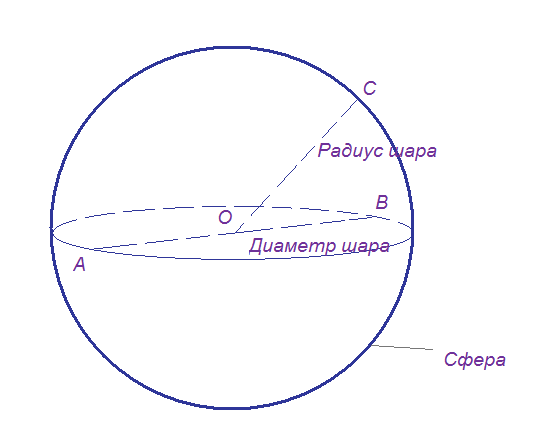
Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Шар – тело, ограниченное сферой.
| Объем шара | Площадь поверхности сферы |
| 
|
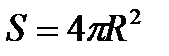
1. Сечение сферы плоскостью есть окружность, если расстояние от центра сферы до плоскости меньше радиуса сферы.
2. Сечение шара плоскостью есть круг.
3. Касательная плоскость к сфере – плоскость, имеющая со сферой только одну общую точку.
4. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
5. Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
6. Многогранник называется описанным около сферы, если сфера касается всех его граней.
7. Отрезки касательных к сфере, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.
8. Сфера вписана в цилиндрическую поверхность, если она касается всех ее образующих.
9. Сфера вписана в коническую поверхность, если она касается всех ее образующих.
Задачи
1. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Ответ: 10.
2. Площадь большого круга шара равна 1. Найдите площадь поверхности шара.
Ответ: 4.
3. Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в два раза?
Ответ: 4.
4. Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен сумме их объемов.
Ответ: 6.
5. Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите площадь его поверхности.
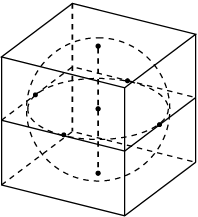Ответ: 96.
6. Куб вписан в шар радиуса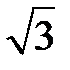 
. Найдите площадь поверхности куба.
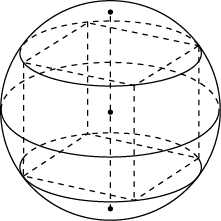Ответ: 24.
7. Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите его объем.
Ответ: 64.
8. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
Ответ: 3.
9. Площадь поверхности прямоугольного параллелепипеда, описанного около сферы, равна 96. Найдите радиус сферы.
Ответ: 2.
10. Около шара описан цилиндр, площадь боковой поверхности которого равна 9. Найдите площадь поверхности шара.
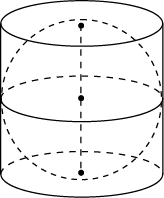Ответ: 9.
11. Во сколько раз площадь поверхности шара, описанного около куба, больше площади поверхности шара, вписанного в этот же куб?
Ответ: 3.
12. Куб вписан в шар радиуса 
. Найдите объем куба.
Ответ: 8.
Составные многогранники
Задачи
1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите расстояние между вершинами A и C2.
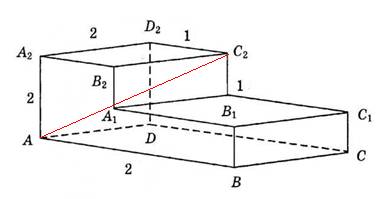Ответ: 3.
2. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
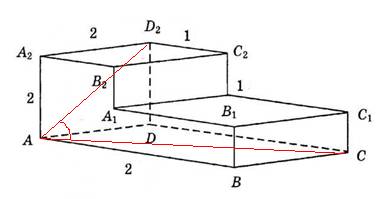Ответ: 60.
3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
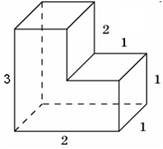Ответ: 18.
4. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 132
5. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
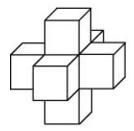Ответ: 30
6. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
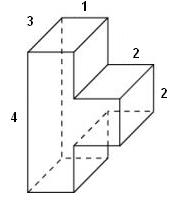Ответ:8
7.Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ: 78
8. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла ABB3.
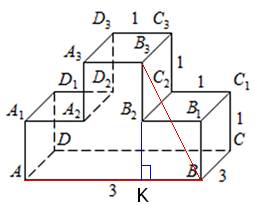Ответ: 2
10. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C3D3B3.
Ответ: 3
11. Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.
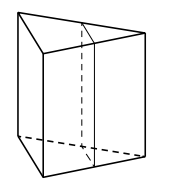Ответ: 74.
12. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами B2 и D3.
Ответ: 11.