Практическое занятие Основы теории графов
Задача 1. а) Для заданного неориентированного графа построить матрицы смежностей и матрицы инцидентностей.
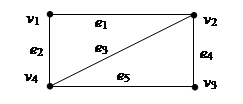
Б) Для заданного ориентированного графа построить матрицы смежностей и матрицы инцидентностей.
. 
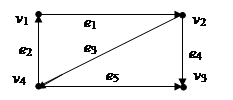
Решение. 1) Строим матрицу смежности вершин, которая будет размерности 4´4. Строим матрицу смежности ребер, которая будет размерности 5´5.
, 
.
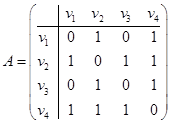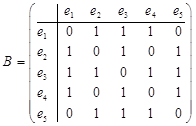Строим матрицу инцидентностей, которая будет размерности 4´5.
.
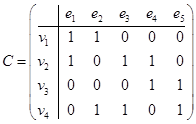2) Строим матрицу смежности вершин, которая будет размерности 4´4. Строим матрицу смежности ребер, которая будет размерности 5´5.
, 
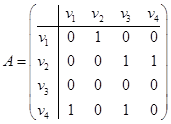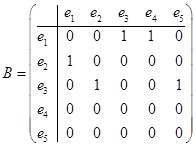
Строим матрицу инцидентностей, которая будет размерности 4´5.
.
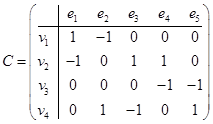В) Построить матрицы смежности и инцидентности для орграфа
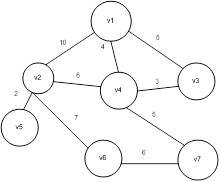
Задача 2. Задать матрицей взвешенный граф, представленный диаграммой
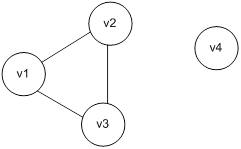
Задача 3 Дан неориентированный граф. Построить его подграф:
А) содержащий вершины 
.
Б)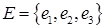 
В) содержащий вершины и ребра
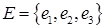
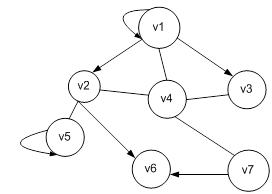
Задача 4 Рассмотрим граф, показанный на рисунке.
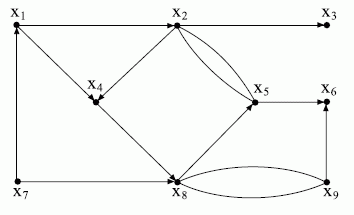
Ориентированный граф
Этот граф определяет следующую систему уравнений:
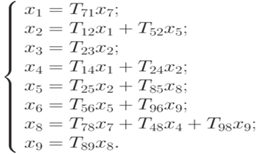
Задача 3а. Структура сети Петри задана четверкой < T, P, I, O >, где T – множество переходов; P – множество позиций; I – входная функция инцидентности; O – выходная функция инцидентности.
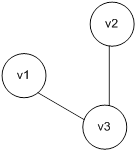
Множество позиций P ={ p 1, p 2}. Множество переходов T ={ t 1, t 2}. Входная функция инцидентности задается комплектами для каждого перехода: I (t 1) = { p 1, p 1} - входные позиции для t 1; I (t 2) = { p 2} - входные позиции для t 2.
Выходная функция инцидентности также задается комплектами для всех переходов сети Петри: O (t 1) = { p 2} - выходные позиции для t 1; O (t 2) = { p 1, p 1, p 1, p 1} – выходные позиции для t2 ..
Надо: построить граф сети Петри.
Данный граф относится к двудольным графам. В нем используются вершины двух типов: позиции и переходы. Позиции связаны только с переходами. Переходы связаны только с позициями. Данный граф имеет следующий вид:
 |
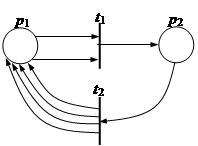Задача 4. Выполнить операции над графами.
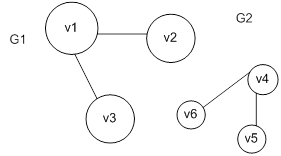
А) объединения
Найти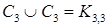 
Б) Пересечения
В) Дополнения
Г) Прямого произведения
Д) Проверить графически справедливость соотношения
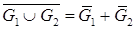
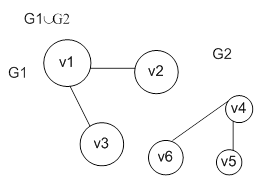
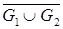
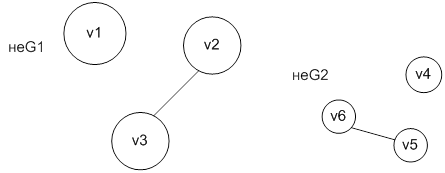
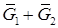
Задача 5 Построить полный двудольный граф K 2,4 и полный граф K 4.
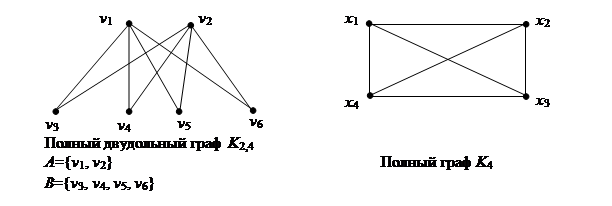
Задача 6. Дан неориентированный граф. Найти расстояние между всеми вершинами графа. Радиус и диаметр графа.
А)
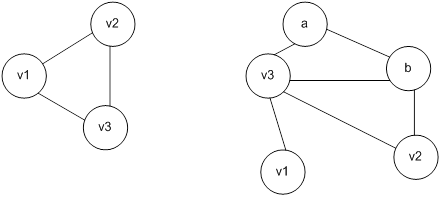
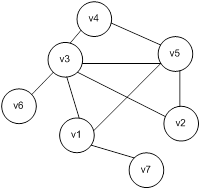
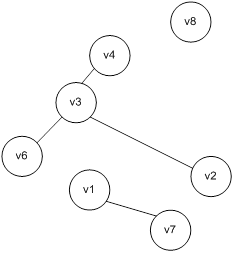
Б) Для графа G, изображенного на рисунке, найти радиус, диаметр и центры.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.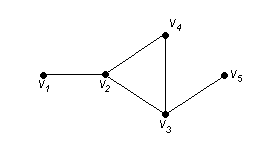 
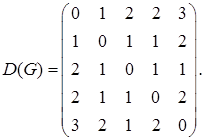
Множество вершин, находящихся на заданном расстоянии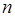 
от вершины 
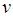, называется ярусом вершины и обозначается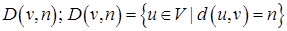 
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: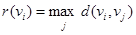 
для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.
Пример Дан неориентированный помеченный граф G 1(V 1; E 1). Построить изоморфные ему графы.
Решение.
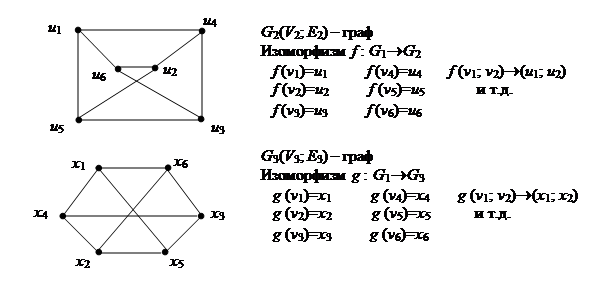
Задача 7. Определить степени вершин данного графа.
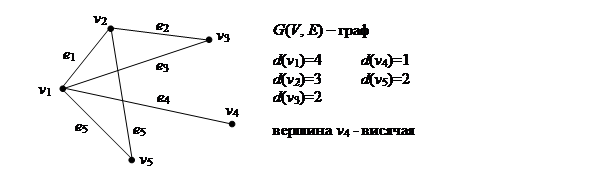
Задача 8. Определить полустепени исхода и захода данного орграфа.
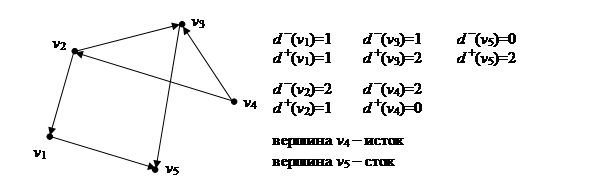
Задача 9. Построить матрицу достижимости для графа
А)
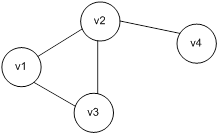
Б)
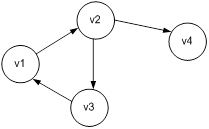
Задача 10. Для неориентированного графа, изображенного на рисунке, найти все маршруты длины 2.
Решение. Составим матрицу смежности вершин P и возведем ее в квадрат. Результат возведения:
.
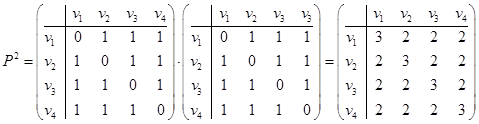Рассмотрим первую строку. Например, элемент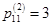 
. Это значит, что существует три маршрута из v 1 в v 1 длиной в два ребра. Действительно, это маршруты 
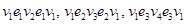. Из v 1 в v 2 существует два маршрута: 
.
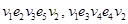Если использовать числовую матрицу смежности вершин, то для нахождения самих маршрутов необходимо работать с графом. Если воспользоваться модифицированной матрицей смежности, в ячейки которой записаны названия ребер, то можно получить не только количество маршрутов, но и сами маршруты.
Действительно, для данного примера имеем
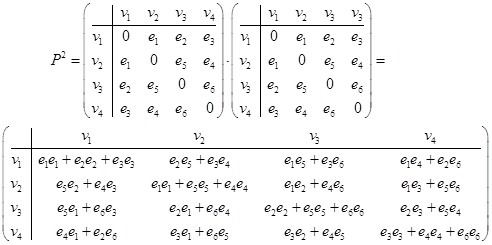
Аналогично обстоит дело с орграфом, хотя у него матрица смежности вершин несимметрическая.
Задача 11. Для орграфа, изображенного на рисунке, найти все маршруты из вершины 1 (2, 3) с тремя дугами.
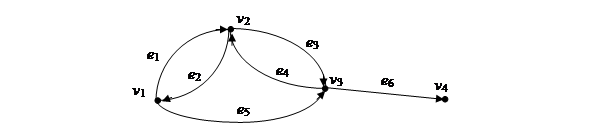
Решение. Матрица смежности P и результаты ее возведения в квадрат и куб имеют следующий вид:
,
.
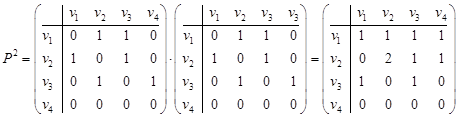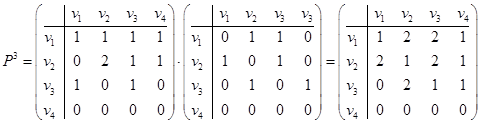Рассмотрим, например, элемент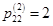 
после возведения матрицы смежности вершин в квадрат. Это значит, из вершины v 2 в вершину v 2 есть два маршрута длиной две дуги. Это маршруты 
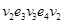и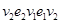 
. После возведения матрицы в куб сохраняется та же картина. Например, 
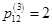. Это значит, что есть два маршрута длиной три дуги из вершины v 1 в вершину v 2. Это маршруты 
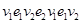и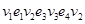 
.
Для получения цепей (маршрутов, в которых каждое ребро встречается один раз) нужно в модифицированной матрице P 3 вычеркнуть те слагаемые, в которых какой-либо сомножитель встречается более одного раза.
Задача 12. Построить остовный граф для графа
А) Остовным деревом называется дерево, содержащее все узлы сети.
Рассмотрим граф с пятью узлами
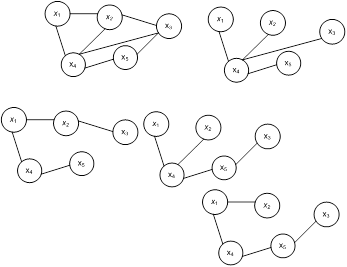
При построении сетей возникает задача построения минимального остовного дерева, т.е задача соединения всех узлов с помощью путей наименьшей длины. Примером такой задачи является задача построения сети дорог.
Рассмотрим процедуру построения минимального остовного дерева. Введем обозначения
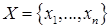- множество узлов сети;
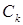- множество узлов сети, соединенных алгоритмом после выполнения 
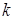-й итерации;
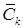- множество узлов сети, не соединенных с узлами множества 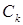после выполнения 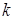-й итерации;
Минимальное остовное дерево сети строят по следующему алгоритму:
1 выбирают произвольный узел сети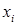 
: 
;
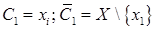2 Выбирают из оставшихся узлов сети узел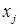 
, ближайший к множеству узлов 
: 
.
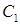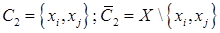3 Выбирают из множества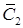 
узел, ближайший к узлам множества 
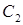и включают его в множество 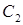и исключают из множества .
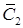За конечное множество шагов будут обработаны все узлы сети и построено минимальное остовное дерево: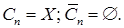 
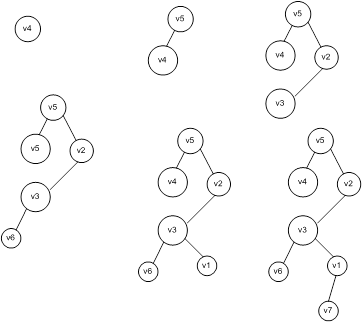
4) Для построения минимального остовного (корневого) дерева рассмотрим взвешенный граф, данный в условии задачи.
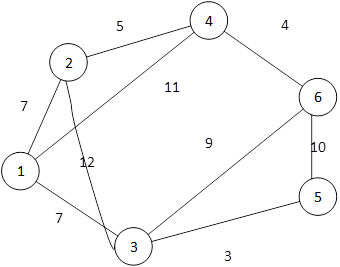
Построим минимальное корневое остовное дерево данного взвешенного графа с помощью алгоритма Прима.
Рассмотрим исходный граф G=<V,E>. Будем строить остов G1=<U,E1>.
| G1 | U | edges | V\U |
| {1} | {(1,2),(1,4),(1,3)} | {2,3,4,5,6} |
| {1,2} | {(1,3),(1,4),(2,3),(2,4)} | {3,4,5,6} |
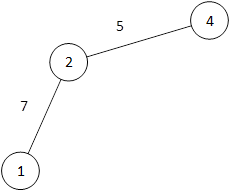
| {1,2,4} | {(1,3),(2,3),(4,6)} | {3,5,6} |
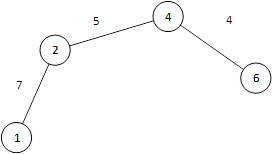
| {1,2,4,6} | {(1,3),(2,3),(6,3),(6,5)} | {5} |
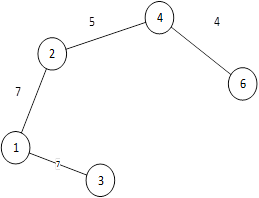
| {1,2,3,4,6} | {(6,5),(3,5)} | {} |
|
Решим задачу с помощью алгоритма Краскала
| G1 | E1 | E\E1 |
| {} | {(1,2),(1,3),(1,4),(2,3),(2,4),(3,6),(3,5),(4,6), (5,6)} | |
| {(3,5)} | {(1,2),(1,3),(1,4),(2,3),(2,4),(3,6),(4,6), (5,6)} |
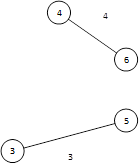
| {(3,5),(4,6)} | {(1,2),(1,3),(1,4),(2,3),(2,4),(3,6), (5,6)} |
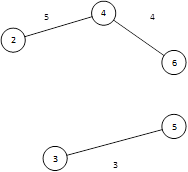
| {(2,4),(3,5),(4,6)} | {(1,2),(1,3),(1,4),(2,3),(3,6), (5,6)} |
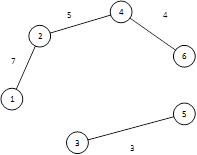
| {(1,2),(2,4),(3,5),(4,6)} | {(1,3),(1,4),(2,3),(3,6), (5,6)} |
|
| {(1,2),(1,3),(2,4),(3,5),(4,6)} |
Алгоритм Дейкстры
Найти минимальное расстояние от истока вершины 1 до вершины 6.
Пометим вершину 1 и на ее основе будем формировать множество вершин, уже посещенных. Пока вершина еще не посещена, будем считать, что от истока до нее расстояние равно. ∞.
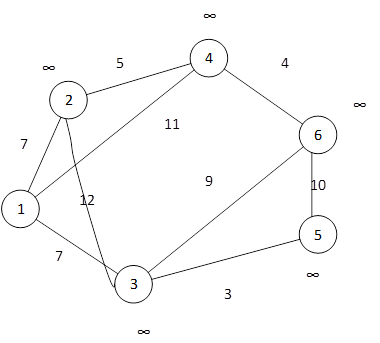
Найдем ближайшую вершину. Сравним расстояние до вершины с выбранным расстоянием. Например вершину 2. Получим расстояние до нее равным 7. Включим данную вершину в множество посещенных вершин. Получим {1,2}.
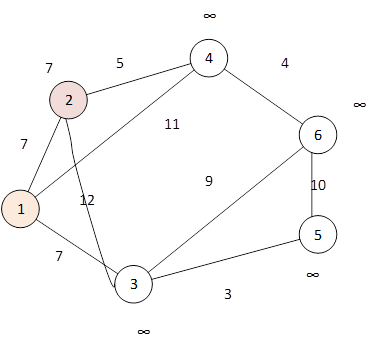
На каждом новом шаге алгоритма оцениваем ближайшие вершины, еще не посещенные. Такой вершиной является вершина 3. Расстояние до нее равно 7. Добавим данную вершину в список уже посещенных вершин.
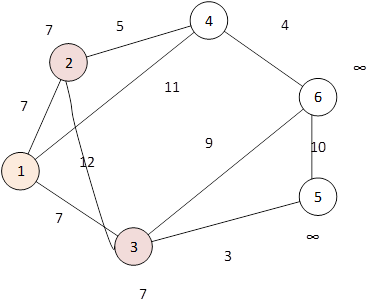
Следующей вершиной из посещенных является вершина 5. Расстояние до нее равно 10.
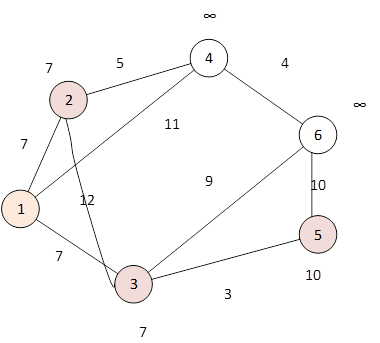
Список посещенных вершин имеет вид {1,2,3,5}.
Следующей вершиной, ближайшей к уже посещенным является вершина 4. Минимальное расстояние до нее min{11,7+5}=11. Включаем ее в множество уже посещенных вершин. Получим список {1,2,3,4,5}.
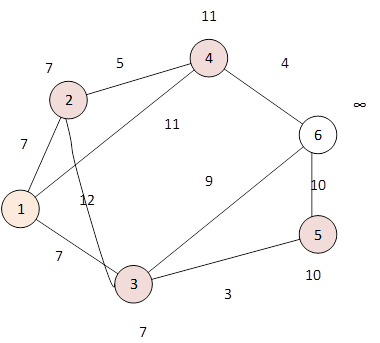
Последняя из непосещенных вершин вершина 6. Расстояние до нее min{∞,11+4,10+10}=15.
Найти цикломатическое число графа.
Пример. Найти компоненты связности для графа
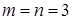
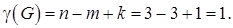
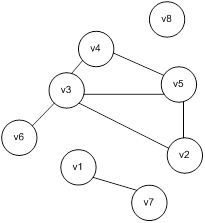
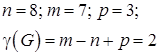
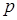- число связных компонент.
Иногда вводят понятие ранга графа
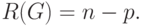
В этом случае цикломатическое число
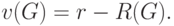
Цикломатическое число графа указывает то наименьшее число рёбер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.
Цикломатическое число всегда неотрицательно.
Основное свойство цикломатического числа формулируется в виде теоремы:
Цикломатическое число мультиграфа равно максимальному числу независимых циклов.
Связность графа
| Номер вершины | Степень вершины |
Для компонент связности
Найти реберную и вершинную связность графа.
Остовный граф
А)
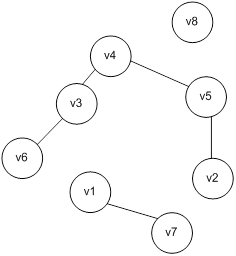
Реберной связностью называется минимальное число ребер, удаление которых приводит к несвязному графу.
Вершинной связностью называется минимальное число вершин, удаление которых приводит к несвязному или тривиальному графу.
Реберная связность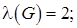 
(нужно удалить два ребра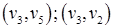 
Вершинная связность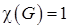 
. (нужно удалить одну вершину 
.)
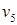Реберная связность обозначается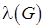 
. Вершинная, 
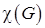. Данные характеристики рассматриваются для компонент связности. Соотношение Уитни:
,
Где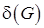 
- минимальная степень вершины.
Построить все остовные графы для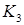 
. 
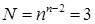
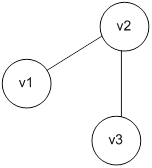
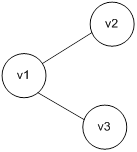
Пример найти эйлеров и гамильтонов циклы для графа.
где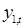 
- расходы на конечное потребление данного года;
- валовые инвестиции в текущем году;
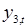- расходы на зарплату в текущем году;
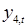- валовый доход в текущем году;
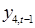- валовый доход предыдущего года;
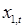- государственные расходы текущего года.
В данной системы использована одна лагированная (предопределенная) переменная 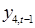с величиной лага, равной единице.
Матрица Кирхгофа — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях)
Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
· Определитель матрицы Кирхгофа равен нулю:
· Матрица Кирхгофа простого графа симметрична:
· Все алгебраические дополнения симметричной матрицы Кирхгофа равны между собой — постоянная матрицы Кирхгофа. Для простого графа значение данной постоянной совпадает с числом всех возможных остовов графа
