Билет №1
1. Объясните, какая фигура называется многоугольником. Что такое вершины, стороны, диагонали и периметр многоугольника?
2. Сформулируйте свойства параллелограмма. Докажите, что в параллелограмме противоположные стороны равны и противоположные углы равны.
Билет №2
1. Какой многоугольник называется выпуклым? Объясните, какие углы называются углами выпуклого многоугольника.
2. Сформулируйте признаки параллелограмма и докажите один из них (по выбору).
Билет №3
1. Выведите формулу для вычисления суммы углов выпуклого n-угольника.
2. Какой четырехугольник называется квадратом? Сформулируйте основные свойства квадрата.
Билет №4
1. Начертите четырехугольник и покажите его диагонали, противоположные стороны и противоположные вершины.
2. Сформулируйте и докажите признак прямоугольника.
Билет №5
1. Чему равна сумма углов выпуклого многоугольника?
2. Сформулируйте свойства прямоугольника и докажите его “особое” свойство.
Билет №6
1. Дайте определение параллелограмма. Является ли параллелограмм выпуклым многоугольником?
2. Какой четырехугольник называется ромбом? Докажите, что диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Билет №7
1. Какой четырехугольник называется трапецией? Как называются стороны трапеции?
2. Сформулируйте свойства параллелограмма и докажите, что диагонали параллелограмма точкой пересечения делятся пополам.
Билет №8
1. Какая трапеция называется равнобедренной? прямоугольной?
2. Какой четырехугольник называется прямоугольником? Докажите, что диагонали прямоугольника равны.
Билет №9
1. Какой четырехугольник называется квадратом? Сформулируйте основные свойства квадрата.
|
|
2. Докажите, что в параллелограмме противоположные стороны равны и противоположные углы равны.
Билет №10
1. Какой четырехугольник называется ромбом? Докажите, что диагонали ромба взаимно перпендикулярны и делят его углы пополам.
2. Чему равна сумма углов выпуклого четырехугольника.
Билет №11
1. Дайте определение параллелограмма. Является ли параллелограмм выпуклым многоугольником?
2. Докажите, что если в параллелограмме диагонали равны, то параллелограмм является прямоугольником.
Билет №12
1. Какой многоугольник называется выпуклым? Объясните, какие углы называются углами выпуклого многоугольника.
2. Докажите, что диагонали параллелограмма точкой пересечения делятся пополам.
Билет №13
1. Какой четырехугольник называется трапецией? Как называются стороны трапеции?
2. Сформулируйте признаки параллелограмма и докажите один и з них (по выбору).
Практическая часть зачета
I вариант
Уровень А:
1. В параллелограмме АВСD найдите:
а) стороны, если ВС на 8 см больше стороны АВ, а периметр равен 64 см;
б) углы, если угол А равен 380.
2. В прямоугольной трапеции один угол 1100, найдите остальные углы.
3. Найдите одну из диагоналей ромба, если один из его углов 600, а периметр равен 16 см.
Уровень В:
1. Дано: АВСD – прямоугольник, 
АВD = 480. Найдите СОD, САD.
2. Периметр параллелограмма 46 см. Найдите стороны параллелограмма, если сумма трех его сторон равна 42 см.
3. Из вершины тупого угла ромба проведен перпендикуляр к его стороне, делящий эту сторону пополам. Найдите углы ромба.
|
|
Уровень С:
1. Дано: ABCD – параллелограмм, AD = 11 см, CD = 4 см. Периметр треугольника BOC равен 26 см. Найдите периметр треугольника АОВ, если точка О – точка пересечения диагоналей параллелограмма.
2. ABCD – прямоугольник (Рисунок4), BE ^ АС, АВ = 12 см, АЕ: ЕС = 1: 3. Найти диагонали прямоугольника.
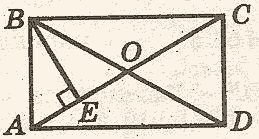
Рисунок 4.
3. В прямоугольной трапеции диагональ перпендикулярна к боковой стороне, острый угол трапеции равен 450. Найдите отношение оснований.
II вариант
Уровень А:
1. Один из углов параллелограмма в три раза больше другого его угла. Найдите все углы параллелограмма.
2. Докажите, что ромб, у которого угол между диагональю и стороной равен 450, является квадратом.
3. В прямоугольнике ABCD диагонали пересекаются в точке О. Е – середина стороны АВ, ВАС = 500. Чему равен ЕОD?
Уровень В:
1. ABCD – параллелограмм, ВЕ – биссектриса АВС; периметр ABCD равен 48 см, АЕ больше ED на 3 см. Найти стороны параллелограмма.
2. ABCD – прямоугольник; АОВ = 360. Найти: CAD, BDC, если точка О – точка пересечения диагоналей прямоугольника.
3. Сторона ромба в два раза больше перпендикуляра, проведенного к ней из вершины тупого угла. Найдите углы ромба.
Уровень С:
1. Дано: ABCD – параллелограмм, точка О – точка пересечения диагоналей параллелограмма, периметр треугольника АОВ равен 21 см, периметр треугольника BOC 24 см, CD = 6 см. Найти периметр параллелограмма ABCD.
2. Дано: ABCD – прямоугольник (Рисунок5), СЕ 
BD, CD = 10 см, DЕ: ОС = 1: 2. Найти диагонали прямоугольника.
Рисунок 5.
3. В равнобедренной трапеции диагональ составляет с боковой стороной угол в 1200. Боковая сторона равна меньшему основанию. Найти углы трапеции.