Если система сверхидентифицирована, то применяется ДМНК. ДМНК заключается в следующем:
1) Составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК.
2) Выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют ДМНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели.
3) Обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.
Пример. Применим ДМНК к простейшей сверхидентифицируемой модели
Слайд 27
,
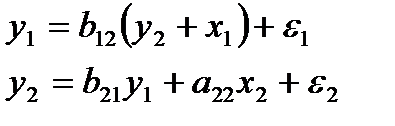которая может быть получена из предыдущей идентифицируемой модели
,
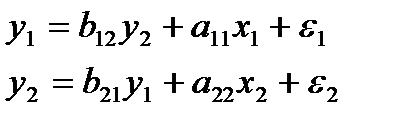если наложить ограничения на ее параметры
.
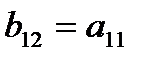В результате первое уравнение стало сверхидентифицируемым:
H=1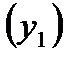 
, D=1 
D+1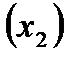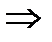>H,т.к. 1+1>1.
Второе уравнение не изменилось и является точно идентифицируемым:
H=1 
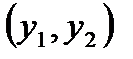, D=1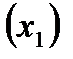 
D+1=H, т.к. 1+1=2.
На первом шаге найдем приведенную форму модели
Слайд 28
.
Используя те же исходные данные, что и в предыдущем примере, получим ту же систему приведенных уравнений:
Слайд 29
.
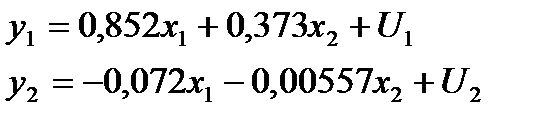На основе второго уравнения данной системы можно найти теоретические значения для эндогенной переменной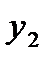 
, т.е. 
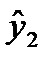. С этой целью в уравнение
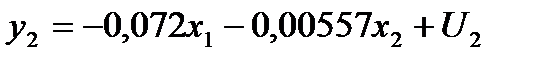
подставим значения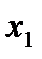 
и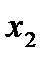 
(в нашем случае это отклонения от средних уровней). Оценки для эндогенной переменной 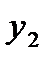занесем в графу 3 вспомогательной табл.3.
Слайд 30
Таблица 3
| 
| 
| 
| 
| 
| 
|
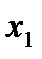
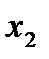
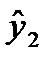
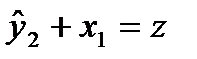
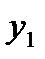
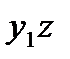
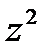
| -1,4 | -0,4 | 0,103 | -1,297 | -2 | 2,594 | 1,682 |
| -0,4 | -2,4 | 0,042 | -0,358 | -1 | 0,358 | 0,128 |
| 0,6 | -1,4 | -0,035 | 0,565 | 0,319 | ||
| -0,4 | 1,6 | 0,020 | -0,380 | -0,380 | 0,144 | |
| 1,6 | 2,6 | -0,130 | 1,470 | 2,940 | 2,161 | |
| ∑0 | 5,512 | 4,434 |
После того, как найдены оценки эндогенной переменной 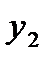, обратимся к сверхидентифицируемому уравнению
.
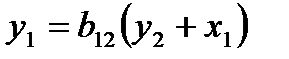Заменяя фактические значения 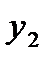их оценками 
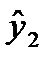, найдем значения новой переменной 
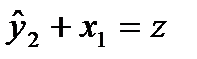и заполним столбец 4 табл.3. Далее применим МНК к уравнению
Слайд 31
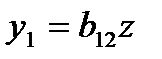, т.е. 
.
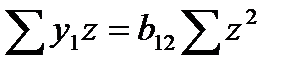Откуда
.
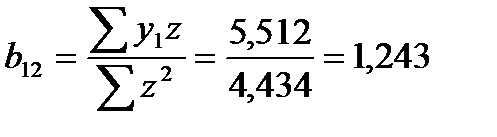Таким образом, сверхидентифицируемое структурное уравнение составит
Слайд 32
.
Ввиду того, что второе уравнение нашей системы не изменилось, то его структурная форма, найденная из системы приведенных уравнений, та же:
.
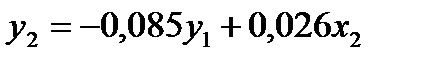В целом рассматриваемая система одновременных уравнений составит
Слайд 33
.
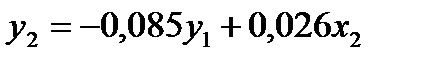Тема 5 Моделирование одномерных временных рядов, автокорреляция в остатках – ЛЕКЦИЯ ВИЗУАЛИЗАЦИЯ
1. Основные элементы временного ряда.
2. Автокорреляция уровней временного ряда.
3. Моделирование тенденции временного ряда.
4. Моделирование сезонных и циклических колебаний.
5. Методы исключения тенденции.
6. Автокорреляция в остатках.
1. Основные элементы временного ряда.
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени (также называют динамический ряд или ряд динамики). Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
- факторы, формирующие тенденции ряда (T);
- факторы, формирующие циклические колебания ряда (S);
- факторы случайные (E).
Большинство временных рядов экономических показателей имеет тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. В совокупности они формируют его возрастающую или убывающую тенденцию. На рис.1 показан гипотетический временной ряд, содержащий возрастающую тенденцию (тренд).
Слайд 1
| y |
| t |
| y |
| t |
| Рис.1 |
| Рис.2 |
Также изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания носят сезонный характер. Например, перевозки пассажиров в летний период возрастают. На рис.2 представлен гипотетический временной ряд, содержащий только сезонную компоненту. Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой случайной компоненты (рис.3).
Слайд 2
| y |
| t |
| Рис.3 |
Очевидно, что реальные данные не следуют целиком и полностью из каких-либо описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент.
Модель, в которой временной ряд представлен как сумма перечисленных компонент, называют аддитивной моделью временного ряда.
Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда.
Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных компонент, с целью использования полученной информации для прогнозирования будущих значений ряда.
2. Автокорреляция уровней временного ряда.
При наличии во временном ряде тенденций и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Рассмотрим расчет коэффициентов автокорреляции уровней для временного ряда расходов на конечное потребление.
Пример. Пусть имеются следующие условные данные о средних расходах на конечное потребление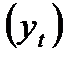 
в денежных единицах за 8 лет (см. табл.1).
Слайд 3
Таблица 1
Расчет коэффициента автокорреляции первого порядка
для временного ряда расходов на конечное потребление, д.е.
| t |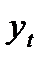 
| 
| 
| 
| 
| 
| 
|
| - | - | - | - | - | - | ||
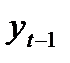
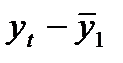
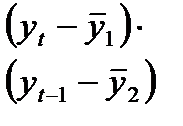
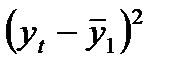
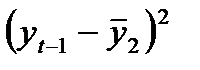
| -3,29 | -3 | 9,87 | 10,8241 | ||||
| -3,29 | -2 | 6,58 | 10,8241 | ||||
| -1,29 | -2 | 2,58 | 1,6641 | ||||
| -0,29 | 0,0841 | ||||||
| 0,71 | 0,71 | 0,5041 | |||||
| 2,71 | 5,42 | 7,3441 | |||||
| 4,71 | 18,84 | 22,1841 | |||||
| ∑ | -0,03* | 44,0 | 53,4287 |
* - сумма не равна нулю ввиду наличия ошибок округления.
Разумно предположить, что расходы на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет.
Определим коэффициент корреляции между рядам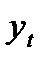и 
и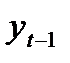 
и измерим тесноту связи между расходами на конечное потребление текущего и предыдущих годов. Добавим в табл.1 временной ряд 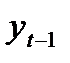(графа 3).
Одна из рабочих формул для расчета коэффициента корреляции имеет вид
Слайд 4
.
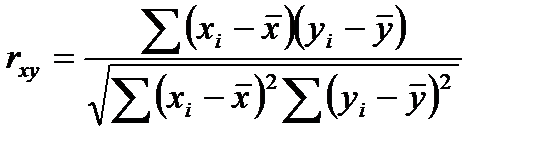В качестве переменной x рассмотрим ряд 
; в качестве переменной y – ряд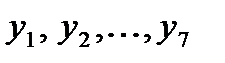 
. Тогда
Слайд 5
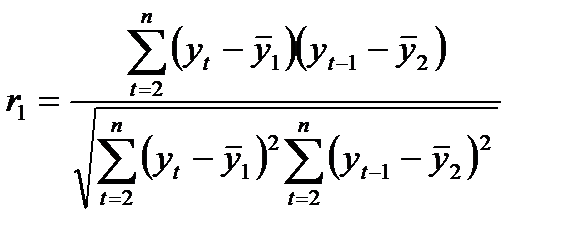, (1)
где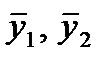 
- коэффициенты автокорреляции уровней ряда первого порядка, т.к. они измеряют взаимосвязь между соседними уровнями ряда t и t- 1, т.е. при лаге 1.
Слайд 6
, 
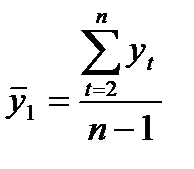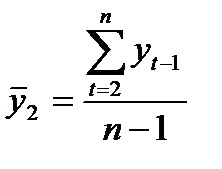. (2)
.
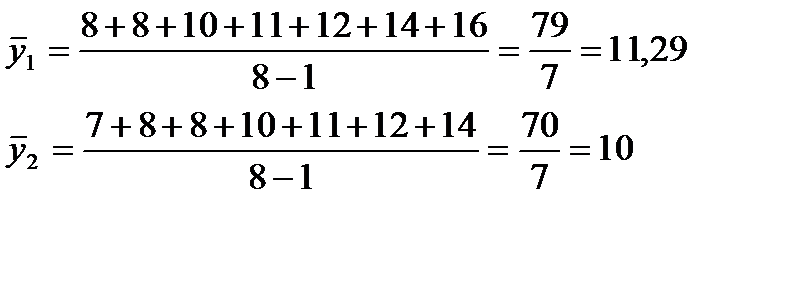Заполняем графы 4-8 табл.1.
Используя (1), рассчитаем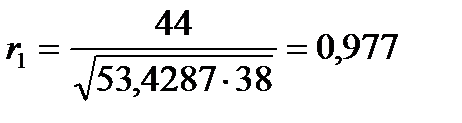 
.
Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующего годов и, следовательно, о наличии во временном ряде расходов на конечное потребление сильной линейной тенденции.
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровням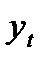и и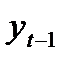 
и определяется по формуле
Слайд 7
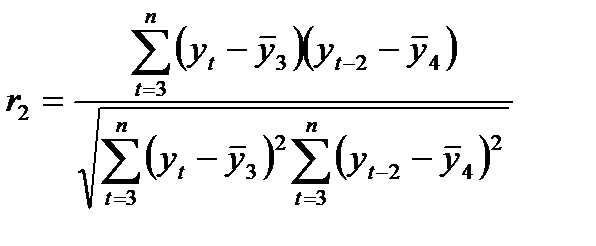, (3)
где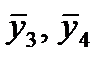 
- коэффициенты автокорреляции уровней ряда второго порядка.
, 
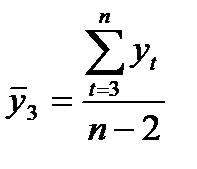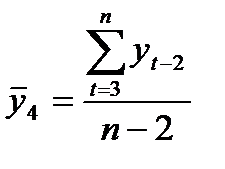. (4)
Для нашего примера получим (графы 1-3, табл.2)
.
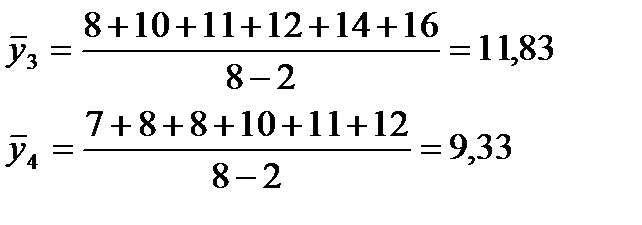Слайд 8
Таблица 2
Расчет коэффициента автокорреляции второго порядка для временного ряда расходов на конечное потребление
| t |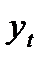
| 
| 
| 
| 
| 
| 
|
| - | - | - | - | - | - | ||
| - | - | - | - | - | - | ||
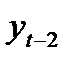
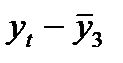
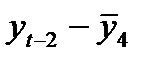
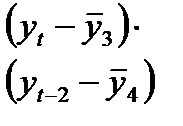
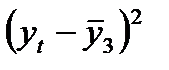
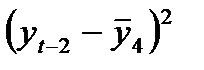
| -3,83 | -2,33 | 8,9239 | 14,6689 | 5,4289 | |||
| -1,83 | -1,33 | 2,4339 | 3,3489 | 1,7689 | |||
| -0,83 | -1,33 | 1,1039 | 0,6889 | 1,7689 | |||
| 0,17 | 0,67 | 0,1139 | 0,0289 | 0,4489 | |||
| 2,17 | 1,67 | 3,6239 | 4,7089 | 2,7889 | |||
| 4,17 | 2,67 | 11,1339 | 17,3889 | 7,1289 | |||
| ∑ | 0,02* | 0,02* | 27,3334 | 40,8334 | 19,3334 |
* - сумма не равна нулю ввиду наличия ошибок округления.
Используя формулу (3), получаем
Слайд 9
.
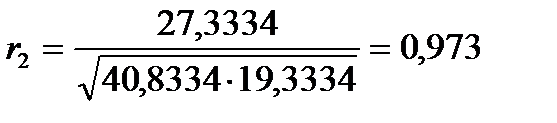Полученные результаты еще раз подтверждают вывод о том, что ряд расходов на конечное потребление содержит линейную тенденцию.
Два важных свойства коэффициента автокорреляции:
1. Он строится по аналогии с линейным коэффициентом корреляции и, таким образом, характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной тенденции.
2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, аграфик зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
3. Моделирование тенденции временного ряда.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяют следующие функции:
Слайд 10
- линейная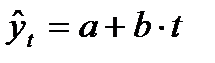 
;
- гипербола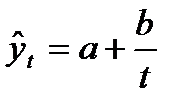 
;
- экспонента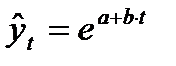 
;
- степенная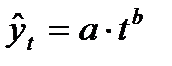 
;
- парабола второго и более высоких порядков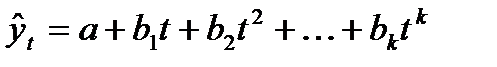 
.
Параметры трендов определяются обычным методом наименьших квадратов, в качестве независимой переменной выступает время t=1,2,…, n, а в качестве зависимой переменной – фактические уровни временной ряда yt.
Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации R2.
4. Моделирование сезонных и циклических колебаний.
Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания.
Простейший подход – расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Общий вид аддитивной модели
. (5)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компоненты.
Общий вид мультипликативной модели
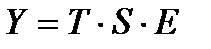. (6)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компоненты. Выбор одной из 2-х моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель.
Построение аддитивной и мультипликативной модели сводится к расчету значений T, S и E для каждого уровня ряда.
Построение модели включает следующие шаги:
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (T+S) в аддитивной или (T·S) в мультипликативной модели.
4. Аналитическое выравнивание уровней (T+E) или (T·E) и расчет значений T с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (T+S) или (T·S).
6. Расчет абсолютных и/или относительных ошибок.
Пример построения аддитивной модели. Пусть имеются условные данные об объемах потребления электроэнергии жителями района за 16 кварталов (см. табл.1).
Слайд 11
Таблица 1.
Потребление электроэнергии жителями района, млн. кВт·ч
| 
| 
| 
|
|
|
|
|
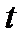
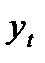
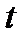
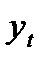
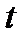
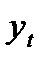
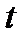
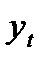
| 6,0 | 7,2 | 8,0 | 9,0 | ||||
| 4,4 | 4,8 | 5,6 | 6,6 | ||||
| 5,0 | 6,0 | 6,4 | 7,0 | ||||
| 9,0 | 10,0 | 11,0 | 10,8 |
Нанесем эти значения на график (см.рис.1).
На графике видно, что временной ряд содержит сезонные колебания периодичностью 4, т.е. можно сделать предположение о возможном существовании в ряде аддитивной модели. Рассчитаем ее компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
а) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим годовые объемы потребления электроэнергии (гр.3 табл.2);
б) разделив полученные суммы на 4, найдем скользящие средние (гр.4 табл.2). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
в) приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр.5 табл.2).
Слайд 12
| Потребление эл/энергии |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 t |
|
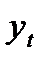
| Рис.1. График потребления электроэнергии за 16 кварталов |
Слайд 13
Таблица 2
Расчет оценок сезонной компоненты в аддитивной модели
| № квартала, t | Потребление электроэнергии, 
| Итого за 4 квартала | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| 6,0 | |||||
| 4,4 | - | - | - | - | |
| 5,0 | 24,4 | 6,10 | - | - | |
| 9,0 | 25,6 | 6,40 | 6,250 | -1,250 | |
| 7,2 | 26,0 | 6,50 | 6,450 | 2,550 | |
| 4,8 | 27,0 | 6,75 | 6,625 | 0,575 | |
| 6,0 | 28,0 | 7,00 | 6,875 | -2,075 | |
| 10,0 | 28,8 | 7,20 | 7,100 | -1,100 | |
| 8,0 | 29,6 | 7,40 | 7,300 | 2,700 | |
| 5,6 | 30,0 | 7,50 | 7,450 | 0,550 | |
| 6,4 | 31,0 | 7,75 | 7,625 | -2,025 | |
| 11,0 | 32,0 | 8,00 | 7,875 | -1,475 | |
| 9,0 | 33,0 | 8,25 | 8,125 | 2,875 | |
| 6,6 | 33,6 | 8,40 | 8,325 | 0,675 | |
| 7,0 | 33,4 | 8,35 | 8,375 | -1,775 | |
| 10,8 |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр.6 табл.2). Используем эти оценки для расчета значений сезонной компоненты S (табл.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si. Здесь предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам равна нулю.
Слайд 14
Таблица 3
Расчет сезонной компоненты в аддитивной модели
| Показатели | Год | № квартала, i | |||
| - | - | -1,250 | 2,550 | ||
| 0,575 | -2,075 | -1,100 | 2,700 | ||
| 0,550 | -2,025 | -1,475 | 2,875 | ||
| 0,675 | -1,775 | - | - | ||
| Итого за i-й квартал (за все годы) | 1,800 | -5,875 | -3,825 | 8,125 | |
Средняя оценка сезонной компоненты для i-го квартала,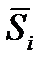 
| 0,600 | -1,958 | -1,275 | 2,708 | |
Скорректированная сезонная компонента,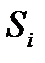 
| 0,581 | -1,977 | -1,294 | 2,690 |
Для данной модели имеем 0,600-1,958-1,275+2,708=0,075 ≠ 0.
Определим корректирующий коэффициент: k =0,075/4=0,01875.
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
,
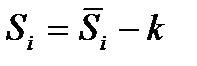где i =1÷4.
(Заполним последнюю строку табл.3.)
Проверим условие равенства нулю суммы значений сезонной компоненты:
0,581-1,977-1,294+2,690=0.
Таким образом, получены следующие значения сезонной компоненты:
Слайд 15
1 квартал S1=0,581;
2 квартал S2=-1,977;
3 квартал S3=-1,294;
4 квартал S4=2,690.
Шаг 3. Элиминируем (исключим) влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T+E=Y-S (гр.4 табл.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Шаг 4. Определим компоненту T (тренд) данной модели. Для этого проведем аналитическое выравнивание ряда (T+E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
Константа a= 5,715416
Коэффициент регрессии b= 0,186421
Стандартная ошибка b mb= 0,015188
R2 =0,91498
Число наблюдений n =16
Число степеней свободы 14.
Таким образом, имеем следующий линейный тренд:
Слайд 16
.
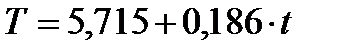Подставляя в это уравнение значения t =1, …16, найдем уровни T для каждого момента времени (гр.5 табл.4).
Слайд 17
Таблица 4
| 
| 
| 
| 
| 
| 
| 
|
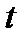
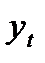
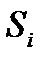
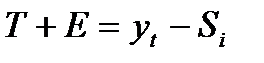
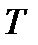
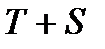
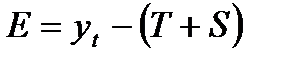
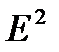
| 6,0 | 0,581 | 5,419 | 5,902 | 6,483 | -0,483 | 0,2333 | |
| 4,4 | -1,977 | 6,377 | 6,088 | 4,111 | 0,289 | 0,0835 | |
| 5,0 | -1,294 | 6,294 | 6,275 | 4,981 | 0,019 | 0,0004 | |
| 9,0 | 2,690 | 6,310 | 6,461 | 9,151 | -0,151 | 0,0228 | |
| 7,2 | 0,581 | 6,619 | 6,648 | 7,229 | -0,029 | 0,0008 | |
| 4,8 | -1,977 | 6,777 | 6,834 | 4,857 | -0,057 | 0,0032 | |
| 6,0 | -1,294 | 7,294 | 7,020 | 5,727 | 0,273 | 0,0745 | |
| 10,0 | 2,690 | 7,310 | 7,207 | 9,896 | 0,104 | 0,0108 | |
| 8,0 | 0,581 | 7,419 | 7,393 | 7,974 | 0,026 | 0,0007 | |
| 5,6 | -1,977 | 7,577 | 7,580 | 5,603 | -0,030 | 0,0009 | |
| 6,4 | -1,294 | 7,694 | 7,766 | 6,472 | -0,072 | 0,0052 | |
| 11,0 | 2,690 | 8,310 | 7,952 | 10,642 | 0,358 | 0,1282 | |
| 9,0 | 0,581 | 8,419 | 8,139 | 8,720 | 0,280 | 0,0784 | |
| 6,6 | -1,977 | 8,577 | 8,325 | 6,348 | 0,252 | 0,0635 | |
| 7,0 | -1,294 | 8,294 | 8,519 | 7,218 | -0,218 | 0,0475 | |
| 10,8 | 2,690 | 8,110 | 8,698 | 11,388 | -0,588 | 0,3457 | |
| ∑=1,10 |
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр.6 табл.4).
Шаг 6. В соответствии с методикой расчет ошибки производится по формуле
.
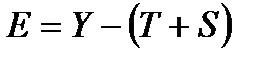Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в гр.7 табл.4.
По аналогии с моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применить сумму квадратов полученных абсолютных ошибок. Для данной задачи ∑=1,10. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня равно 71,59. Эта величина составляет чуть более 1,3%.
(1-1,10/71,59)·100=1,397.
Следовательно, можно сказать, что аддитивная модель объясняет 98,7% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
Слайд 18
.
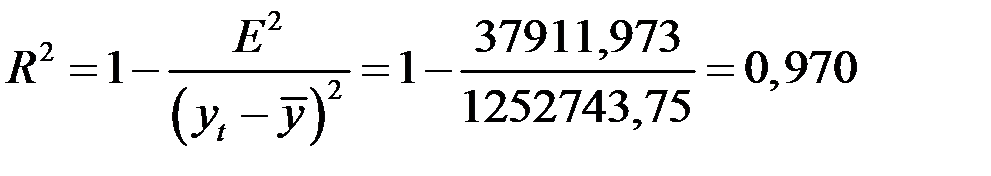Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года.
5. Методы исключения тенденции.
При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.
Метод отклонений от тренда
предполагает вычисление трендовых значений для каждого временного ряда модели, например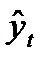 
и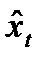 
, и расчет отклонений от трендов: 
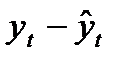и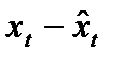 
. Для дальнейшего анализа используют не исходные данные, а отклонения от тренда.
Метод последовательных разностей
заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:
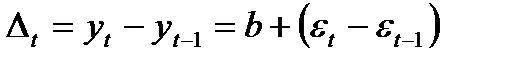; (7)
если параболический тренд – вторыми разностями:
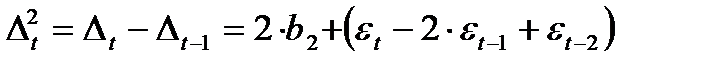. (8)
В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.
Модель, включающая фактор времени, имеет вид
. (9)
Параметры a и b в этой модели определяются обычным МНК.
6. Автокорреляция в остатках.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков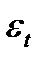 
за текущий и предыдущий моменты времени.
Автокорреляция остатков может быть вызвана несколькими причинами, имеющими разную причину.
Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.
Во-вторых, - формулировка модели. Модель может не включать фактор, оказывающий существенное воздействие на результат, влияние которого отражается в остатках. Очень часто этим фактором является фактор времени t.
Существует два метода определения автокорреляции остатков.
Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции.
Второй метод – использование критерия Дарбина - Уотсона и расчет величины
Слайд 19
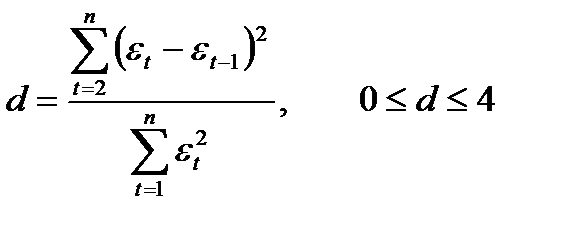. (10)
Таким образом, d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Коэффициент автокорреляции остатков первого порядка определяется по формуле
Слайд 20
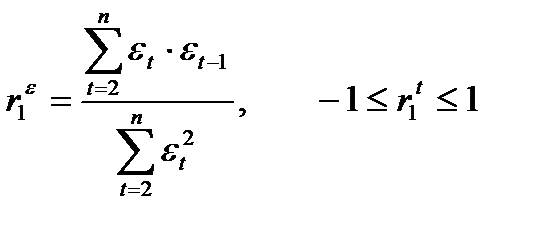, (11)
Критерий Дарбина - Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением
Слайд 21
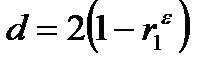. (12)
Таким образом, если в остатках существует полная положительная автокорреляция
и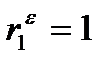 
, то d =0.
Если в остатках полная отрицательная автокорреляция, то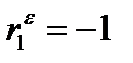 
и, следовательно, d =4.
Если автокорреляция остатков отсутствует, то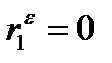 
и, следовательно, d =2.
Если фактическое значение критерия Дарбина – Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют нулевую гипотезу об отсутствии автокорреляции остатков.