ЗАДАНИЕ №1. Линейная алгебра.
Решить заданную систему: а) пользуясь формулами Крамера;
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 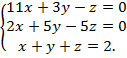
Решение типового примера.
Пусть требуется решить систему уравнений: 
Решение:
а) Метод Крамера. Подсчитаем главный определитель системы, для этого воспользуемся разложением определителя системы по элементам первой строки по формуле:
 =
= 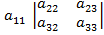 --
--  +
+ 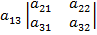
Вычислим главный определитель системы
 =1
=1  +2
+2  +1
+1  =10
=10
Так как  =10, не равен нулю, система имеет единственное решение. Вычислим вспомогательные определители:
=10, не равен нулю, система имеет единственное решение. Вычислим вспомогательные определители:
 =
=  =1 3 2 +
=1 3 2 +  +1
+1  8 -
8 -  3 1 -8
3 1 -8  2 - 1
2 - 1  =
=
6-2-8+3+32-1=30.
Аналогично находим
 =
= 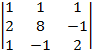 =0
=0  =
= 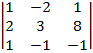 =-20
=-20
Согласно формулам Крамера имеем:
X=  =
=  =3; y=
=3; y=  =0; z=
=0; z=  =-2.
=-2.
Для проверки правильности решения подставим его в каждое уравнение системы

Ответ:  .
.
ЗАДАНИЕ №2. Векторная алгебра.
В задачах 21-40 даны координаты вершин пирамиды АВСД.
Требуется:
1. Записать координаты векторов  ,
,  и
и  , найти их длины;
, найти их длины;
2. Найти угол между векторами  и
и  ;
;
3. Составить уравнение ребра АС;
4. Составить уравнение грани АВС.
21.А  , В
, В 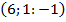 , С
, С  , Д
, Д  .
.
22. А  , В
, В  , С
, С  , Д
, Д  .
.
23.А  , В
, В  , С
, С  , Д
, Д  .
.
24. А 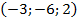 , В
, В  , С
, С 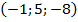 , Д
, Д  .
.
25. А  , В
, В  , С
, С  , Д
, Д  .
.
26. А  , В
, В  , С
, С  , Д
, Д  .
.
27. А  , В
, В  , С
, С  , Д
, Д  .
.
28. А  , В
, В  , С
, С  , Д
, Д  .
.
29. А  , В
, В  , С
, С  , Д
, Д  .
.
30. А  , В
, В 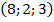 , С
, С 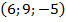 , Д
, Д  .
.
31. А 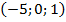 , В
, В  , С
, С  , Д
, Д  .
.
32. А  , В
, В 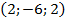 , С
, С  , Д
, Д  .
.
33. А  , В
, В 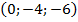 , С
, С  , Д
, Д  .
.
34. А  , В
, В  , С
, С  , Д
, Д  .
.
35. А  , В
, В  , С
, С  , Д
, Д  .
.
36. А  , В
, В  , С
, С  , Д
, Д  .
.
37. А  , В
, В  , С
, С  , Д
, Д 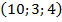 .
.
38. А 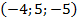 , В
, В  , С
, С  , Д
, Д  .
.
39. 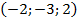 , В
, В  , С
, С 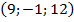 , Д
, Д  .
.
40. А  , В
, В  , С
, С  , Д
, Д  .
.
Решение типового примера.
Пусть А(0;0;1), В(2;3;5), С(6;2;3), D(3;7;2).
1. Известно, что произвольный вектор  , заданный координатами точек
, заданный координатами точек  (
( и
и  имеет координаты, которые определяются по формуле
имеет координаты, которые определяются по формуле  .
.
Следовательно

 ,
, 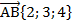
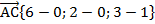 ,
, 
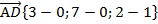 ,
,  .
.
Если  , то длина вектора определяется формулой
, то длина вектора определяется формулой
 =
=  . Тогда
. Тогда
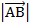 =
=  =
=  ;
;
 =
=  =
=  =2
=2 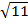 ;
;
 =
= 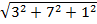 =
= 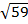 .
.
2. Известна формула  =
= 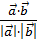 где числитель – скалярное произведение векторов
где числитель – скалярное произведение векторов  =
=  . Тогда
. Тогда
 =
=  =
=  0,7279.
0,7279.
По тригонометрическим таблицам определяем, что  43
43  .
.
3. Уравнение прямой, проходящей через две заданные точки  (x1;y1;z1) и М2
(x1;y1;z1) и М2  , имеет вид:
, имеет вид:
 =
=  =
=  ,
,
Тогда уравнение ребра АС имеет вид
 =
=  =
=  или
или  =
=  или АС:
или АС:  .
.
4. Уравнение плоскости, проходящей через три заданные точки  (x1;y1;z1),
(x1;y1;z1),
М2  ,
,  имеет вид
имеет вид
 =0
=0
Подставим координаты точек А,В,С в заданную формулу и получим
 =0;
=0;
Вычислим определитель третьего порядка
 =0
=0
6x+24y+4  -18
-18  -4y-8x=0;
-4y-8x=0;
-2x+20y-14  =0;
=0;
-2x+20y-14z+14=0;
x-10y+7z-7=0.
ЗАДАНИЕ №3. Интегральное исчисление.
В задачах 61-80 вычислить площадь, ограниченную параболами.
61. а) y=  x2-x+1, y=
x2-x+1, y=  x2+3x+6. б) y=2x2, y=-2x+4.
x2+3x+6. б) y=2x2, y=-2x+4.
62. а) y=  x2+x+6, y=-
x2+x+6, y=-  x2-5x+7. б) y=x2, y=-x+2.
x2-5x+7. б) y=x2, y=-x+2.
63. а) y=  x2-3x+2, y=-
x2-3x+2, y=-  x2-2x+4. б) y=3x2, y=-x+4.
x2-2x+4. б) y=3x2, y=-x+4.
64. а) y=2x2+6x-3, y=-x2+x+5. б) y=  x2, y=-x+3.
x2, y=-x+3.
65. а) y=3x2-5x-1, y=-x2+2x+1 б) y=  x2, y=-3x+12.
x2, y=-3x+12.
66. а) y=x2-3x-1, y=-x2-2x+5. б) y=  x2, y=-3x+12.
x2, y=-3x+12.
67. а) y=2x2-6x+1, y=-x2+x-1, б) y=4x2, y=-2x+2.
68. а) y=  x2-2x+4, y=-
x2-2x+4, y=-  x2-x+2, б) y=
x2-x+2, б) y=  x2, y=-
x2, y=-  x+2.
x+2.
69. а) y=x2-5x-3, y=-3x2+2x-1, б) y=4x2, y=-2x+6.
70. а) y=x2-2x-5, y=-x2-x+1, б) y=x2, y=-x+3.
71. а) y=  x2-2x-5, y=-
x2-2x-5, y=-  x2-x+1, б) y=2x2, y=-3x+14.
x2-x+1, б) y=2x2, y=-3x+14.
72. а) y=  x2+3x-2, y=-
x2+3x-2, y=-  x2-x+3, б) y=
x2-x+3, б) y=  x2, y=-x+6.
x2, y=-x+6.
73. а) y=2x2-6x+3, y=-2x2+x+5, б) y=3x2, y=-2x+5.
74. а) y=x2-3x-4, y=-x2-x+8, б)y=  x2, y=-2x+9.
x2, y=-2x+9.
75. а) y=  x2-3x-1, y=-
x2-3x-1, y=-  x2-x+2, б) y=
x2-x+2, б) y=  x2, y=-2x+6.
x2, y=-2x+6.
76. а) y=2x2+4x-7, y=-x2-x+1, б) y=2x2, y=-x+10.
77. а) y=2x2+3x+1, y=-x2-2x+9, б) y=3x2, y=-3x+6.
78. а) y=2x2-6x-2, y=-x2+x-4, б) y=x2, y=-2x+5.
79. а) y=x2-2x-4, y=-x2-x+2, б) y=  x2, y=-x+3.
x2, y=-x+3.
80. а) y=  x2-3x-2, y=-
x2-3x-2, y=-  x2-7x+3, б) y=3x2, y=-5x+8.
x2-7x+3, б) y=3x2, y=-5x+8.
Решение типового примера.
Вычислить площадь, ограниченную параболами
у=2х2-х-2; у=-х2+х-1;
Решение:
В декартовой системе координат построим заданные параболы.
Найдем точки пересечения графика функции у=2х2-х-2 с осью Ох, решив уравнение 2х2-х-2=0, где а=2,в=-1,с=-2. Вычислим дискриминант
D=в2-4ас. D=  2
2  =17
=17
Х=  , Х1=
, Х1=  Х2=
Х2= 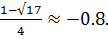
Найдём координаты вершины параболы Х0=  , Х0=
, Х0=  =0.25, У0=2
=0.25, У0=2 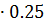 2-0.25-2=-2.4.
2-0.25-2=-2.4.
Найдем точки пересечения графика функции у=-х2+х-1 с осью Ох, решив уравнение -х2+х-1=0. D=12-4  =-3
=-3  0, следовательно точек пересечения параболы с осью Ох нет. Так как а=-1
0, следовательно точек пересечения параболы с осью Ох нет. Так как а=-1  0, ветви параболы направлены вниз.
0, ветви параболы направлены вниз.
Найдем координаты вершины параболы Х0=  =0,5,
=0,5,
У0=-0,252+0,5-1=-0,75.
Строим схематически графики заданных функций.
Найдем абсциссы точек пересечения парабол, решив уравнение
2х2-х-2=-х2+х-1
3х2-2х-1=0
D=4, х1=1, х2=--  .
.
При х=1 у=-1; х=-  у=-1
у=-1  .
.
Вычисление площади осуществляем по формуле
S=  , где
, где  – кривые, ограничивающие фигуру
– кривые, ограничивающие фигуру  .
.
S=  =
=  =
=  =
=  .
.
Ответ: Искомая площадь  квадратных единиц.
квадратных единиц.
| Номер варианта | Задание №1 | Задание №2 | Задание №3 | Задание №4 |
Общие методические указания.
Заочная форма обучения предполагает самостоятельную работу студента над учебным материалом: работа с учебником, разбор и решение типовых задач, выполнение контрольной работы.
Если возникли затруднения при самостоятельном изучении материала, студент может обратиться к преподавателю для получения устной или письменной консультации.
Чтобы получить письменную консультацию, студент должен точно указать характер затруднений, название учебника или задачника, год издания и страницу, где находится вызвавший затруднения вопрос или задача.
Студенты, в соответствии с действующим учебным планом, изучают курс высшей математики в течение одного семестра и выполняют одну контрольную работу.
При выполнении контрольной работы студент должен руководствоваться следующими указаниями:
1.Работа выполняется в отдельной тетради в клетку, на титульном листе которой должны быть ясно написаны фамилия студента, его инициалы, домашний адрес;
2.Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением задачи надо полностью переписать её условие;
3.Ход решения каждой задачи студент должен оформлять аккуратно, в полном соответствии с порядком решения типовой задачи, приведенной в данных методических указаниях;
4.Решение задач геометрического содержания должно сопровождаться чертежами, с указанием осей координат и единиц масштаба. Пояснения к задачам должны соответствовать обозначениям, приведённых на чертежах;
5. На каждой странице тетради необходимо оставлять поля шириной 3-4см для замечаний преподавателя;
6.В случае незачёта по контрольной работе студент обязан в кратчайшие сроки исправить все отмеченные преподавателем ошибки и недочеты и предъявить работу на повторное рецензирование, приложив при этом первоначально выполненную работу;
7.Студент выполняет тот вариант контрольной работы, который совпадает с номером по учебному журналу в соответствии с таблицей