ЗАДАНИЯ НА КОНТРОЛЬНЫЕ РАБОТЫ
Методические указания.
Контрольная работа выполняется в отдельной тетради или на листах формата А4 в соответствии с требованиями данной контрольной работы.. Работа должна иметь титульный лист.
В начале работы указывается номер варианта, который определяется студентом, как остаток от деления на 9 числа из двух последних цифр зачетной книжки. Например, номер зачетки - 98144, тогда 44 делится на 9 и номер варианта - 8. Если остаток от деления равен нулю, то номер варианта принимается равным 10.
После проверки контрольной работы она возвращается студенту с отметкой “зачет”, если же работа не зачтена, она дорабатывается студентом и сдается на повторную проверку. Все исправления и добавления помещаются в той же тетради, что и основная работа, но не в тексте основной работы, а в конце.
Контрольная работа № 1 (часть 1)
Содержание контрольной работы
1. Определить номер варианта контрольной работы и привести полный текст задания.
2. Решить первую и вторую задачу варианта. Комментировать шаги решения. Выделить результат, полученный по данному алгоритму.
3. Во второй задаче варианта рассматривается одноканальная СМО с отказами. В данную СМО поступает пуассоновский поток заявок. Время между моментами поступления двух последовательных заявок распределено закону f(x). Время обслуживания заявок случайное и распределено по закону f1(t). Найти методом Монте-Карло за время Т: а) среднее число обслуженных заявок, б) среднее время обслуживания одной заявки, г) вероятность отказа. Произвести шесть испытаний.
Пример выполнения контрольной работы дан в приложении 2.
Задания для контрольной работы № 1
Вариант 1.
1. Смоделировать восемь возможных значений дискретной случайной величины Х, закон распределения которой задан в виде таблицы:
| Х | ||||
| р | 0.2 | 0.12 | 0.43 | 0.25 |
2. f(x) = 0,1exp(-0,1x), f1(t) = exp(-t), T = 10 мин
Вариант 2.
1. Смоделировать шесть опытов по схеме Бернулли: опыт состоит из четырех испытаний, в каждом из которых вероятность появления события А равна 0.5.
2. f(x) = 0,2exp(-0,2x), f1(t) =1,1 exp(-1,1t), T = 15 мин
Вариант 3.
1. Смоделировать пять опытов по схеме Бернулли: опыт состоит из трех независимых испытаний, в каждом из которых вероятность появления события А равна 0.4.
2. f(x) = 0,2exp(-0,2x), f1(t) = 1,2exp(-1,2t), T = 20 мин
Вариант 4.
1. Найти явную формулу для моделирования непрерывной случайной величины Х, распределенной равномерно в интервале (а, в), зная ее функцию распределения
F(x) = (x-a)/(b-a), а <x< в.
2. f(x) = 0,3exp(-0,3x), f1(t) = 1,4exp(-1,4t), T = 25 мин
Вариант 5.
1. Смоделировать четыре возможных значения непрерывной случайной величины Х, распределенной равномерно в интервале (4, 14).
2. f(x) = 0,4exp(-0,4x), f1(t) = 1,5exp(-1,5t), T = 30 мин
Вариант 6.
1. Найти явную формулу для моделирования непрерывной случайной величины Х, распределенной по показательному закону, заданному функцией распределения F(x) = 1- exp(-ax).
2. f(x) = 0,5 exp(-0,5x), f1(t) = 1,2exp(-1,2t), T = 15 мин
Вариант 7.
1. Найти явную формулу для моделирования непрерывной случайной величины Х, заданной плотностью вероятности f(x) = b/(1+ax)2 в интервале [ 0, 1/(b-а)], вне этого интервала f(x) =0.
2. f(x) = 0,6exp(-0,6x), f1(t) = 1,3exp(-1,3t), T = 20 мин
Вариант 8.
1. Смоделировать пять возможных значений непрерывной случайной величины Х, заданной плотностью вероятности f(x) = 10/(1 + 2x)2 в интервале [ 0. 1/8], вне этого интервала f(x) =0.
2. f(x) = 0,7 exp(-0,7x), f1(t) = 1,4exp(-1,4t), T = 25 мин
Вариант 9.
1. Найти явную формулу для моделирования непрерывной случайной величины Х, заданной плотностью вероятности f(x) = 2 в интервале (0, 0,5), вне этого интервала f(x) =0.
2. f(x) = 0,2exp(-0,2x), f1(t) = 2exp(-2t), T = 10 мин t
Вариант 10.
1. Разыграть пять возможных значений непрерывной случайной величины Х, распределенной по показательному закону, заданному плотностью вероятности F(x) = 0,1 exp(-0,1x) в интервале (0, ~), вне этого интервала f(x) =0.
2. f(x) = 0,8exp(-0,8x), f1(t) =2,5 exp(-2,5t), T = 30 мин
Контрольная работа № 1 (часть 2)
Содержание контрольной работы
1. Определить номер варианта и привести полный текст задания.
2. В первой задаче варианта необходимо определить, потоком Эрланга какого порядка можно заменить рассматриваемый поток, для которого известны математическое ожидание и среднеквадратическое отклонение.
3. Во второй задаче определите тип СМО, нарисуйте граф переходов для данной СМО, проверьте стационарность СМО, рассчитайте требуемые характеристики СМО.
4. В третьей задаче построить граф передач для описанной сети СМО, построить матрицу передач, рассчитать интенсивности потоков для каждой СМО, проверить стационарность сети, и если сеть не стационарна, подобрать необходимое количество каналов в соответствующих СМО и добиться не стационарности сети.
Пример выполнения контрольной работы дан в приложении 2.
Вариант 1
3. mt = 4 мин, d t = 1 мин
4. Интенсивность прихода заявок в одноканальную СМО равна 5, интенсивность обслуживания - 6, Очередь в СМО не ограничена. Найти:
а) вероятность того, что в системе находится ровно три заявки,
б) вероятность занятости системы,
в) вероятность отказа,
г) вероятность того, что есть требования в очереди,
д) среднее время ожидания в очереди.
5. Партии комплектующих деталей поступают в цех сборки в среднем каждую минуту. В этом цеху изделие собирается целиком и отправляется в отдел технического контроля для проверки. При проверке изделий признаются годными только 40%, остальные требуют доработки, Причем часть негодных изделий имеют мелкие недоработки и отправляются в цех наладки, после которого снова попадают в ОТК, а часть негодных изделий имеют серьезные неполадки, допущенные при сборке и отправляются снова в цех сборки. Соотношение этих изделий составляет 5:1 соответственно. На сборку одного изделия затрачивается в среднем 3 мин. На проверку качества - 30 сек. и на наладку - 2 мин.
Вариант 2
1. mt = 5,5 мин, d t = 2 мин
2.Два рабочих обслуживают группу из шести станков. Остановки каждого работающего станка происходят в среднем каждые полчаса. Процесс наладки занимает в среднем 10 мин.
Определить:
а) среднее число занятых рабочих,
б) среднее количество неисправных станков,
в) вероятность того, что все станки исправны,
г) среднее время простоя станка из-за неисправности.
3. Больные приходят в поликлинику в среднем каждые 5 мин. и обращаются в регистратуру за талоном к врачу или за карточкой. Регистратор обслуживает посетителя среднем в течение 3 мин. После регистратуры больной направляется к врачу. Врач осматривает больного и назначает лечение. В 40% случаев больному достаточно одного визита к врачу, а в 50% - врач назначает время повторного посещения больного, в остальных случаях пациент направляется на сдачу анализов, после чего он снова должен прийти к врачу. Все повторные посещения врача проходят без обращения в регистратуру. Врачу выделяется на каждого больного в среднем 12 мин. Анализы производятся в течение одного часа.
Вариант 3
1. mt = 8 мин, d t = 3 мин
2. Одноканальная СМО с отказами представляет собой одну телефонную линию. Заявка-вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов - 0,8 (вызовов в мин.). Средняя продолжительность разговора - 1,5 мин. Определить:
а) относительную пропускную способность,
б) абсолютную пропускную способность,
в) вероятность отказа.
3. В почтовое отделение посетители заходят в среднем через каждые 4 мин. Примерно 60% посетителей направляются в отдел переводов (получить перевод, отправить заказное письмо, оформить подписку), а остальные приходят для отправления/получения посылки или бандероли и для этого направляются в соответствующий отдел. Среди клиентов, отправляющих посылки, около 20% вынуждены повторно обратиться в этот же отдел (неправильно заполненные бланки и т.д.). После отдела отправки посылок 40% посетителей направляются в отдел переводов. Будем считать, что после отдела переводов все клиенты покидают почтовое отделение. Среднее время обслуживания в отделе переводов -3 мин., в отделе посылок - 6 мин.
Вариант 4
1. mt = 3,5 мин, d t = 1,5 мин
2. Автозаправочная станция содержит три заправочные колонки. Поток машин, прибывающих для заправки, имеет интенсивность 2 маш./мин. Процесс заправки продолжается в среднем 1 мин.
а) среднее число машин, ожидающих заправки,
б) среднее число машин на станции,
в) среднее время ожидания машин в очереди,
г) среднее время пребывания на станции.
3. В аэропорт заходят пассажиры в среднем каждые 40 сек. Половина из них имеет на руках билеты и сразу же направляется на регистрацию, другая половина не имеет билетов и поэтому сначала обращается в кассу аэропорта. Кассир обслуживает каждого клиента в среднем 2 мин., причем билеты приобретают только 80% человек, остальные получают отказ из-за отсутствия мест и после этого покидают аэропорт. Пассажиры, купившие билет, направляются на регистрацию. Регистрация билетов производится в среднем в течение одной минуты. После регистрации, ожидая посадки в самолет, часть пассажиров (около 30%) направляется в буфет, остальные просто находятся в зале ожидания. Буфетчица обслуживает клиентов в среднем 3 мин.
Вариант 5
1. mt = 4 мин, d t = 1 мин1,2
2. Рабочий обслуживает группу из трех станков. Каждый станок останавливается в среднем в среднем 2 раза в час. Процесс наладки занимает в среднем 8 мин.
Определить:
а) вероятность занятости рабочего,
б) его абсолютную пропускную способность,
в) среднее количество неисправных станков,
г) среднее время простаивания станка.
3. В предварительных железнодорожных кассах работают кассы и справочная служба. Посетители заходят в кассы примерно каждые 5 мин., причем 60% посетителей направляется сразу в кассу, а остальные - в справочную службу. Справочная обслуживает каждого клиента в среднем 3 мин. В зависимости от полученной справки (есть или нет места на нужные поезда и т.д.) посетители либо направляются в кассу (около 70%), либо уходят. На работу с клиентом кассир затрачивает в среднем 7 мин. При этом 60% посетителей приобретают билеты и уходят, половина оставшихся направляется кассиром в справочную службу, а вторая половина вынуждена прийти в кассу в следующий раз, когда будет получена информация или бронь.
Вариант 6
1. mt = 10 сек, d t = 3 сек
2. На автозаправочной станции находится две заправочные колонки. Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно, поток машин, прибывающих для заправки, имеет интенсивность 2 маш./мин. Время обслуживания одной машины составляет в среднем 1 мин. Найти:
а) вероятность отказа
б) среднее число занятых колонок,
в) среднее число машин в очереди,
г) абсолютную пропускную способность станции.
3. После первичной термообработки в печи детали поступают в цех доводки, в котором проходят два этапа обработки и технический контроль. Время обработки детали на первом этапе составляет 7 сек., на втором - 8 сек. При выходе из цеха детали проверяются контролером ОТК. Около 80% деталей пропускается контролером, а 20% направляется повторную обработку в цех, причем половина из них отправляется на первый этап обработки, половина - на второй (в зависимости от степени брака). Время между поступлениями деталей в цех равно в среднем 10 сек., время технического контроля - 5 сек.
Вариант 7
1. mt = 7 мин, d t = 1 мин
2. На авторемонтной станции работают трое рабочих. Интенсивность поступления машин на ремонт составляет две машины в день. Среднее врямя ремонта одной машины - 1 день. Если кто-то из рабочих свободен, то он помогает товарищам.
Определить:
а) вероятность того, что на ремонте находится только одна машина,
б) среднее число машин, находящихся в ремонте,
в) вероятность того, что каждый рабочий ремонтирует отдельную машину.
3. В магазине находится два отдела и касса, общая для двух отделов. Покупатели заходят в магазин в среднем каждые 2,5 мин. Половина из них направляется в первый отдел, вторая половина - во второй. После первого отдела около 60% покупателей направляется сразу в кассу и после этого покидает магазин, остальные направляются во второй отдел. После второго отдела около 40% покупателей направляются в кассу и покидают магазин, остальные заходят еще и в первый отдел. Среднее время обслуживания в первом отделе - 4 мин., во втором - 3,5 мин., кассир обслуживает покупателей в среднем за 2 мин.
Вариант 8
1. mt = 4 мин, d t = 1 мин
2. На железнодорожную сортировочную горку прибывают составы с интенсивностью 2 состава в час. Среднее время, в течении которого горка обрабатывает состав, равна 0,4 часа. Составы, пришедшие в момент, когда горка занята, становятся в очередь. Найти:
а) среднее число составов, ожидающих в очереди,
б) среднее время ожидания состава,
в) среднее время нахождения состава на станции
г) вероятность того, что сортировочная станция будет простаивать в ожидании очередного состава.
3. На станции обслуживания выполняются следующие услуги: заправка бензина, мойка машин, мелкий ремонт, Примерно 60% машин, прибывающих на станцию, направляются на заправку бензина, половина оставшихся - на мойку, остальные нуждаются в мелком ремонте. После мойки все машины уезжают, эта операция занимает около 15 мин. После мелкого ремонта половина машин уезжает, а половина направляется на заправку бензина. После заправки бензина половина машин также уезжает, а вторая половина направляется на мойку. Машины прибывают на станцию в среднем каждые 30 мин, заправка бензина длится 5 мин.
Вариант 9
1. mt = 4 мин, d t = 1 мин
2. Интенсивность прихода заявок в двухканальную СМО с отказами равна 4, интенсивность обслуживания - 3.
Найти:
а) вероятность того, что в системе нет ни одной заявки,
б) среднее время обслуживания,
в) среднее количество заявок в системе,
г) среднее время пребывания в системе.
3. В оптике, где посетитель может заказать или купить очки, работает врач-окулист, Посетители, которые приходят в среднем каждые 5 мин., могут либо сразу обратиться в отдел заказов на очки, либо пройти к врачу за рецептом (40% посетителей).Врач затрачивает на каждого посетителя в среднем 5 мин., причем в продаже могут оказаться подходящие для клиента очки, тогда он их покупает и покидает оптику, 80% клиентов вынуждены заказывать индивидуальное изготовление очков. На выполнение заказа в мастерской оптики требуется в среднем около одного часа, после чего клиент может получить свои очки через отдел заказов.
Вариант 10
1. mt = 6 мин, d t = 2,5 мин
2. На авторемонтной станции работают трое рабочих. Интенсивность поступления машин на ремонт составляет 5 машин в день. Среднее врямя ремонта одной машины - 2 дня. Если кто-то из рабочих свободен, то он помогает товарищам. Если на станции есть уже 3 машины, то очередная машина получает отказ.
Определить:
а) вероятность отказа,
б) вероятность того, что каждый рабочий ремонтирует отдельную машину.
в) абсолютную пропускную способность станции,
г) вероятность того, что все рабочие свободны.
3. В аптеке есть два отдела: отдел готовых лекарств и рецептурный отдел. Посетители приходят в аптеку в среднем через каждые 2,5 мин. Половина посетителей направляется в отдел готовых лекарств, после чего покидает аптеку. Вторая половина посетителей обращается в рецептурный отдел. В 50% случаев клиент сразу же получает готовое лекарство по рецепту, в остальных случаях готового лекарства нет, и клиент должен зайти еще раз за изготовленным лекарством. После рецептурного отдела 20% посетителей заходит еще и в отдел готовых изделий, остальные покидают аптеку. Время обслуживания в отделе готовых лекарств 2 мин, в рецептурном отделе - 5 мин.
Контрольная работа № 2
Содержание контрольной работы
1. Определить номер варианта и привести полный текст задания.
2. Перейти от позиционной к нормальной форме игры. При этом определяются множества чистых стратегий игроков, а затем строится платежная матрица. Решить игру любым известным методом.
Пример выполнения контрольной работы дан в приложении 2.
Вариант 1
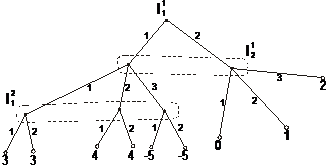
Вариант 2
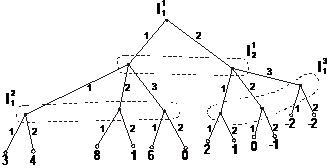
Вариант 3
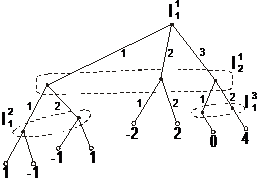
Вариант 4
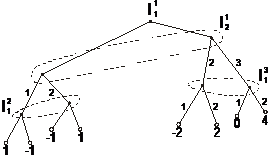
Вариант 5

Вариант 6

Вариант 7
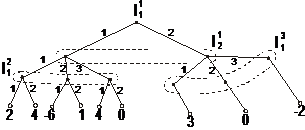
Вариант 8
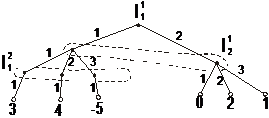
Вариант 9

Вариант 10
