Методические указания
Тема 1. Проверка соответствия выборки нормальному закону
1 Постановка задачи
Дана случайная выборка объема n =100:
| 104.6 | 95.2 | 82.0 | 107.7 | 116.8 | 80.0 | 100.8 | 124.6 | 99.4 | 101.4 |
| 100.6 | 86.3 | 88.2 | 103.8 | 98.5 | 111.8 | 83.4 | 94.7 | 113.6 | 74.7 |
| 114.3 | 86.9 | 106.6 | 94.9 | 105.9 | 88.6 | 96.6 | 93.7 | 90.8 | 96.5 |
| 110.2 | 100.0 | 95.6 | 102.9 | 91.1 | 103.6 | 94.8 | 112.8 | 100.1 | 95.3 |
| 113.9 | 113.9 | 86.1 | 110.3 | 88.4 | 97.7 | 70.1 | 100.5 | 90.9 | 94.5 |
| 109.1 | 82.2 | 101.9 | 86.7 | 97.4 | 102.1 | 87.2 | 94.71 | 112.4 | 94.9 |
| 111.8 | 99.0 | 101.6 | 97.2 | 96.5 | 102.7 | 98.6 | 100.0 | 86.2 | 89.4 |
| 85.0 | 86.6 | 122.7 | 101.8 | 118.3 | 106.1 | 91.3 | 98.4 | 90.4 | 95.1 |
| 93.1 | 110.4 | 100.4 | 86.5 | 105.4 | 96.9 | 101.9 | 83.8 | 107.3 | 107.5 |
| 113.7 | 102.8 | 88.7 | 112.5 | 79.4 | 79.1 | 98.1 | 103.8 | 107.2 | 102.3 |
2 Теоретическая часть
Под случайной выборкой объема n понимают совокупность случайных величин 
, не зависимых между собой. Случайная выборка есть математическая модель проводимых в одинаковых условиях независимых измерений.
Упорядоченной статистической совокупностью будем называть случайную выборку величины в которой расположены в порядке возрастания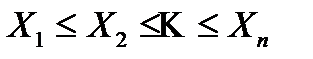 
.
Размах выборки есть величина r=Xn-X1, где Xn - max, X1 - min элементы выборки.
Группированным статистическим рядом называется интервалы с соответствующими им частотами на которые разбивается упорядоченная выборка, причем ширина интервала находится как:
тогда частота попадания в отрезок 
находим по формуле:
, где Vi - число величин попавших в отрезок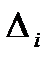 
, причем 
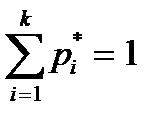. Поделив каждую частоту на 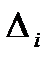получим высоту для построения гистограммы.
Построив гистограмму мы получили аналог кривой распределения по которой можем выдвинуть гипотезу о законе распределения. Выровнять статистическое распределение с помощью закона о котором выдвинули гипотезу, для этого нужно статист. среднее m x* и статистическую дисперсию D x*.
Которые находим как
Естественной оценкой для мат. ожидания является среднее арифметическое значение:
.
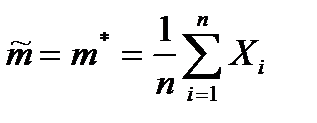Посмотрим, является ли эта оценка не смещенной, для этого найдем ее математическое ожидание:
,
то есть оценка 
для m является несмещенной.
Найдем дисперсию этой оценки:
Эффективность или неэффективность оценки зависит от вида закона распределения случайной величины X. Если распределение нормально, то оценка 
для мат. ожидания m является и эффективной.
Перейдем к оценке для дисперсии D. На первый взгляд наиболее естественной представляется статистическая дисперсия D *, то есть среднее арифметическое квадратов отклонений значений Xi от среднего:
.
Проверим состоятельность этой оценки, выразив ее через среднее арифметическое квадратов наблюдений:
.
, где правая часть есть среднее арифметическое значений случайной величины X2 сходится по вероятности к ее мат. ожиданию: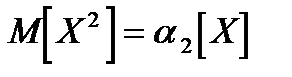 
. Вторая часть сходится по вероятности к 
; вся величина сходится по вероятности к 
. Значит, оценка состоятельна.
Проверим ее на несмещенность, подставив в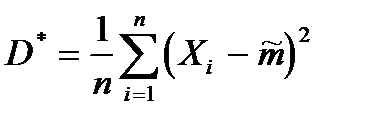 
вместо 
его выражение и произведем действия:
.
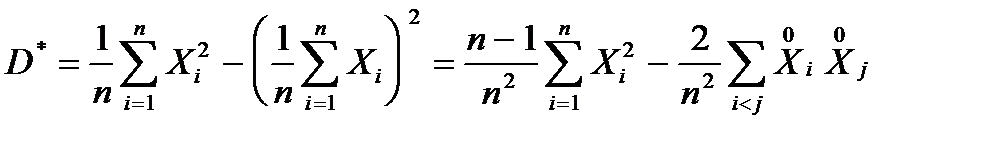Так как D* не зависит от выбора начала координат то отцентрируем все случайные величины . Тогда
.
Найдем мат. ожидание величины D*:
.
Но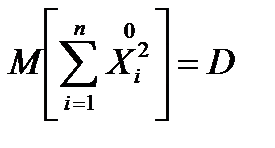 
, 
, и получаем:
.
Отсюда видно, что величина D* не является несмещенной оценкой для дисперсии D; ее мат. ожидание не равно D, а несколько меньше. Пользуясь оценкой D* вместо D, будет проходить систематическая ошибка в меньшую сторону, чтобы ее ликвидировать введем поправку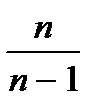 
тогда мы получим несмещенную оценку для дисперсии:
При больших n поправочный коэффициент 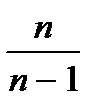становится близким к единицы, и его применение теряет смысл. Поэтому в качестве приближенных значении (оценок) этих характеристик нужно взять:
,
.
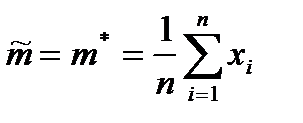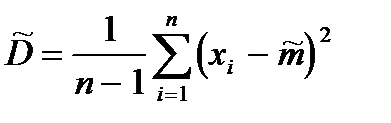3 Практическая часть
Упорядоченная выборка 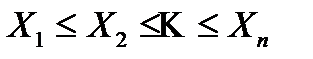где n=100 количество замеров:
| 70.1 | 74.7 | 79.1 | 79.4 | 80.0 | 82.0 | 82.2 | 83.4 | 83.8 | 85.0 |
| 86.1 | 86.2 | 86.3 | 86.5 | 86.6 | 86.7 | 86.9 | 87.2 | 88.2 | 88.4 |
| 88.6 | 88.7 | 89.4 | 90.4 | 90.8 | 90.9 | 91.1 | 91.3 | 93.1 | 93.7 |
| 94.5 | 94.7 | 94.7 | 94.8 | 94.9 | 94.9 | 95.1 | 95.2 | 95.3 | 95.6 |
| 96.5 | 96.5 | 96.6 | 96.9 | 97.2 | 97.4 | 97.7 | 98.1 | 98.4 | 98.8 |
| 98.6 | 99.0 | 99.4 | 100.0 | 100.0 | 100.1 | 100.4 | 100.5 | 100.6 | 100.8 |
| 101.4 | 101.6 | 101.8 | 101.9 | 101.9 | 102.1 | 102.3 | 102.7 | 102.8 | 102.9 |
| 103.6 | 103.8 | 103.8 | 104.6 | 105.4 | 105.9 | 106.1 | 106.6 | 107.2 | 107.3 |
| 107.5 | 107.7 | 109.1 | 110.2 | 110.3 | 110.4 | 111.8 | 111.8 | 112.4 | 112.5 |
| 112.8 | 113.0 | 113.6 | 113.9 | 113.9 | 114.3 | 116.8 | 118.3 | 122.7 | 124.6 |
Размах выборки r=Xn-X1 =124.6-70.1= 54.5
На основе выше изложенной теории для исследования статистики составляем табл. 1.
Табл. 1
| Интервалы | Число попаданий в интервал | Частота попаданий в интервал 
| Высоты интервалов для гистограммы |
| 1. 70.10 - 75.55 2. 75.55 - 81.00 3. 81.00 - 86.45 4. 86.45 - 91.90 5. 91.90 - 97.35 6. 97.35 - 102.80 7. 102.80 - 108.25 8. 108.25 - 113.70 9. 113.70 - 119.15 10. 119.15 - 124.60 | 23.5 13.5 | 0.020 0.030 0.080 0.150 0.170 0.235 0.135 0.110 0.050 0.020 | 0.0036697 0.0055045 0.0146788 0.0275229 0.0311926 0.0431192 0.0247706 0.0201834 0.0091743 0.0036697 |
| Сумма 1.000 |
По построенной гистограмме (рис. 3.1) можно предположить, что данное распределение подчиняется нормальному закону. Для подтверждения выдвинутой гипотезы проведем оценку неизвестных параметров, для мат. ожидания
,
для оценки дисперсии
.
Полагая в выражении нормальной плотности
, где 
и пользуясь, либо приложением 4 в учебнике Вентцель Е.С., Овчаров Л.А.” Прикладные задачи теории вероятностей.”, либо как в нашем случае воспользоваться системой MathCad, получим значения на границах разрядов табл. 2:
Табл. 2
| x | f(x) |
| 1. 70.10 2. 75.55 3. 81.00 4. 86.45 5. 91.90 6. 97.35 7. 102.80 8. 108.25 9. 113.70 10.119.15 11.124.60 | 0.0010445 0.0036354 0.0097032 0.0198601 0.0311717 0.0375190 0.0346300 0.0245113 0.0133043 0.0055377 0.0017676 |
и построим выравнивающую ее нормальную кривую рис. 1
Рассчитаем вероятность (табл.3) попадания с. в. Х в k -й интервал по формуле
Табл. 3.3
| 
|
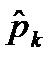
| 1. 70.10 - 75.55 2. 75.55 - 81.00 3. 81.00 - 86.45 4. 86.45 - 91.90 5. 91.90 - 97.35 6. 97.35 - 102.80 7. 102.80 - 108.25 8. 108.25 - 113.70 9. 113.70 - 119.15 10. 119.15 - 124.60 | 0.0115694 0.0344280 0.0790016 0.1398089 0.1908301 0.2009057 0.1631453 0.1021833 0.0493603 0.0183874 |
Для проверки правдоподобия гипотезы воспользуемся критерием согласия 
для этого возьмем данные из табл. 3.1 и 3.3 и подставим в формулу:
Рис. 1
Определяем число степеней свободы (10-1- l)=7, где l - число независимых условий (количество параметров подлежащих оценки в нашем случаи их l= 2, это mx, Dx - для нормального распределения). По приложению 3 в учебнике Вентцель Е.С., Овчаров Л.А. ”Теория вероятностей и ее инженерные приложения.”находим при r=7, p=0.95 
=2.17 для уровня значимости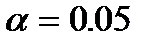 
и видим, что 
, но даже меньше.
Это свидетельствует о том, что выдвинутая нами гипотеза о нормальности распределения не противоречит опытным данным.
Задание 1.
Вариант номеp - 1
4.959 5.119 5.622 4.475 6.843 4.280 3.883 5.431 4.585 6.190
4.760 4.197 4.816 6.727 3.646 3.195 4.752 5.916 4.639 6.113
5.439 4.174 6.797 4.161 6.005 5.566 4.382 4.320 5.910 5.049
3.115 3.586 6.198 5.724 4.422 6.228 5.743 4.089 2.689 4.034
4.501 3.284 7.507 5.561 5.761 5.346 3.923 5.386 5.394 3.454
4.694 4.355 4.102 6.184 5.532 2.834 4.670 5.754 4.356 4.958
4.215 5.279 6.543 3.882 5.436 5.017 6.177 5.030 3.864 5.620
6.297 4.346 4.111 4.386 3.153 4.544 5.122 5.508 3.448 4.357
4.424 5.321 5.593 4.787 6.377 4.557 5.959 4.356 4.420 5.591
5.120 5.356 6.328 5.693 4.109 6.098 5.455 5.278 3.666 4.162
Вычисления проводить с точностью до 0.001
Вариант номеp - 2
-24.920 -25.960 -22.840 -22.920 -24.400 -22.880 -23.400 -24.480 -25.880 -24.960
-22.120 -22.080 -22.640 -23.840 -24.560 -23.760 -22.920 -25.840 -22.240 -22.560
-25.920 -22.920 -25.800 -22.680 -22.280 -24.280 -22.680 -24.800 -25.120 -25.920
-23.600 -22.280 -25.120 -25.520 -24.720 -24.320 -23.080 -25.720 -23.560 -23.760
-22.320 -23.760 -25.800 -23.200 -24.440 -23.960 -22.840 -23.560 -25.520 -24.840
-23.600 -22.520 -25.440 -24.120 -22.040 -25.080 -25.840 -23.080 -25.920 -23.440
-23.440 -22.960 -22.840 -23.040 -24.080 -25.560 -22.160 -25.040 -22.120 -24.720
-23.560 -24.880 -24.960 -22.480 -24.680 -22.920 -24.600 -22.400 -24.240 -24.600
-22.960 -24.720 -23.800 -24.520 -22.080 -25.200 -25.680 -25.520 -24.000 -24.000
-24.840 -25.320 -22.360 -25.400 -22.080 -23.800 -22.840 -23.800 -22.360 -25.560
Вычисления проводить с точностью до 0.001
Вариант номеp - 3
-1.290 -2.294 1.089 -2.463 -3.126 -1.096 -3.107 -2.094 -2.849 -3.446
-4.270 -5.458 -4.559 -6.230 -4.781 -8.380 0.271 -4.026 -6.024 -4.005
-5.466 -3.355 -7.638 -0.040 -9.753 -3.928 -6.763 -6.013 -3.703 -0.897
-3.296 -5.514 -4.807 -2.106 -5.137 -0.452 -11.185 -9.342 -3.439 -1.303
-3.837 0.420 -7.860 -2.357 -5.891 -8.239 -0.811 -7.973 -3.854 -5.429
-5.707 -1.824 -0.862 -6.201 -5.218 -3.152 -6.931 -3.797 -3.517 -6.012
0.796 -4.901 -4.531 -2.528 -2.203 -1.889 -5.191 -6.141 -6.081 -8.077
-3.681 -5.856 -7.868 -8.974 -1.692 -1.496 -4.724 -6.528 -3.664 -5.949
-2.187 -0.381 -7.046 -2.422 -7.424 -5.116 -4.536 -6.685 -1.481 -4.505
-1.341 -0.328 -1.534 -1.764 -2.417 -8.005 -3.137 -0.800 0.272 -6.686
Вычисления проводить с точностью до 0.001
Вариант номеp - 4
-3.085 -0.905 -2.935 -0.461 -2.927 -1.810 -3.489 -2.523 -1.788 -0.908
-1.411 -0.062 -1.791 -1.676 -2.392 -4.591 -1.632 -1.102 -3.570 -1.011
0.669 -1.436 -0.286 -2.360 -0.983 -2.940 -3.826 -0.560 -1.506 -1.637
-1.178 -1.173 -4.394 -2.062 -1.779 -1.145 -2.465 -2.012 -1.265 -1.560
-3.609 -1.296 -1.219 -3.390 -2.542 -1.483 -0.927 -1.241 -2.555 -1.656
-2.121 -2.107 -2.261 -1.159 -2.734 -2.120 -2.350 -2.347 -2.649 -3.297
-2.333 -1.336 -0.445 -3.292 -2.297 -1.757 -2.153 -0.145 -3.655 -1.498
-3.003 -2.036 -3.890 -0.464 -3.173 -2.027 -0.312 -2.317 -3.542 0.179
-1.806 -1.233 -1.435 -2.505 -2.578 -2.651 -1.380 -1.303 -2.912 -3.018
-1.852 -3.327 -1.913 -1.546 -2.025 -2.325 -2.263 -2.958 -2.525 -0.432
Вычисления проводить с точностью до 0.001
Вариант номеp - 5
13.763 3.015 2.203 3.015 7.349 2.300 5.138 0.660 1.475 0.286
1.220 8.198 8.428 18.615 3.576 3.460 2.700 5.590 10.925 17.680
15.451 8.198 4.444 2.108 4.993 2.700 2.014 1.304 0.895 11.266
2.203 6.241 4.852 0.508 1.830 0.895 4.713 5.908 6.414 24.546
32.236 0.584 1.389 3.460 4.713 12.004 0.213 0.895 14.282 3.813
7.152 5.908 12.828 4.993 8.428 14.842 2.497 2.803 0.213 8.911
2.203 2.497 3.813 12.404 5.908 6.414 5.908 4.713 32.236 2.108
0.975 3.576 12.828 0.433 8.911 10.599 0.975 6.591 6.073 5.908
6.773 0.584 9.990 0.070 10.599 5.747 4.444 1.138 0.433 1.389
9.990 13.763 0.895 1.220 8.911 5.908 0.975 7.761 13.280 7.976
Вычисления проводить с точностью до 0.001
Вариант номеp - 6
-15.496 -7.211 -9.065 -7.298 -8.144 -7.298 -4.579 -5.821 -7.627 -7.627
-1.049 0.930 -8.616 -6.935 -1.049 -8.071 -11.067 -17.947 0.930 -5.405
-2.310 -6.194 -7.627 -9.364 -7.705 -17.947 -11.067 -10.179 -8.373 -16.141
-5.405 -11.814 0.141 -5.255 -9.926 -9.261 -3.743 -5.549 -5.821 -9.364
-7.211 -6.531 -7.030 -3.971 5.831 -2.310 -8.789 1.947 -5.950 -12.763
-9.261 -11.067 -10.903 -7.856 -12.763 -7.856 -7.705 -13.353 -9.806 -7.856
-9.806 -9.926 -7.929 -6.636 -5.097 -7.384 -13.690 -5.097 -0.504 -11.814
-10.451 -7.705 -6.074 -5.821 -10.595 -7.627 -2.647 -5.950 -21.831 -10.312
-6.194 3.380 -9.469 -3.971 -7.929 -9.065 -8.878 -6.074 -8.295 -2.954
-10.050 -8.970 -16.930 -9.161 1.947 -5.688 -5.821 -5.688 -6.739 -12.501
Вычисления проводить с точностью до 0.001
Вариант номеp - 7
13.583 13.833 17.230 16.527 14.844 18.417 15.869 18.554 16.527 15.527
17.742 16.881 12.362 10.642 15.418 17.557 17.944 17.557 17.156 16.421
16.947 18.417 12.788 15.119 14.986 19.027 17.557 16.087 16.582 14.056
13.711 15.361 15.527 14.613 15.243 16.582 18.858 16.697 22.828 15.182
18.700 16.818 15.053 13.711 14.353 15.823 15.527 18.167 16.131 16.000
13.833 19.887 14.986 16.271 14.443 15.243 14.353 17.647 15.913 18.554
11.829 14.160 19.414 16.043 15.303 11.115 14.353 13.947 20.885 16.224
12.973 15.303 12.113 11.829 14.844 16.947 16.087 24.299 16.473 14.160
21.968 15.182 22.828 15.119 17.307 15.182 20.171 16.582 15.053 15.361
16.818 14.770 16.881 17.840 15.579 17.944 19.887 18.858 15.119 13.142
Вычисления проводить с точностью до 0.001
Вариант номеp - 8
12.263 7.166 -1.657 6.599 13.893 -4.597 -4.597 9.226 20.996 8.705
14.028 12.447 10.107 1.284 12.740 14.774 14.167 13.893 6.285 17.401
19.275 8.320 7.895 2.231 15.887 0.064 12.640 18.055 12.086 9.226
11.360 12.542 7.166 22.716 6.892 21.769 10.723 15.295 28.597 7.166
11.260 11.360 15.483 11.360 18.424 10.606 9.689 11.553 10.107 9.972
5.172 9.059 19.775 12.086 7.895 10.836 12.947 3.658 11.458 -4.597
14.614 11.360 15.887 6.892 11.737 7.666 19.275 8.320 12.354 12.447
9.972 10.946 14.028 10.107 12.354 18.424 12.542 23.936 18.055 14.167
7.166 11.360 11.158 12.740 13.763 12.947 13.277 11.914 3.658 12.447
20.996 11.914 13.164 7.423 13.277 4.225 13.394 11.827 7.895 5.945
Вычисления проводить с точностью до 0.001
Вариант номеp - 9
-7.100 -12.000 -8.400 -6.800 -4.900 -13.200 -9.900 -12.200 -10.900 -11.800
-13.100 -4.100 -6.000 -5.200 -10.400 -4.900 -7.100 -5.100 -9.100 -7.300
-13.700 -11.700 -5.300 -11.200 -10.100 -4.800 -13.100 -12.800 -10.500 -10.400
-9.200 -4.100 -12.200 -7.500 -12.000 -5.700 -10.200 -10.000 -12.900 -6.400
-11.700 -13.100 -12.000 -8.500 -10.600 -13.200 -10.400 -5.400 -4.800 -7.000
-8.200 -6.800 -10.500 -12.500 -4.500 -13.700 -12.900 -13.700 -12.700 -11.100
-11.200 -6.600 -13.300 -7.900 -13.200 -12.200 -12.700 -6.200 -12.100 -10.200
-4.600 -13.600 -4.800 -13.700 -7.600 -7.200 -11.100 -4.200 -10.600 -7.100
-7.700 -10.700 -5.300 -12.500 -9.200 -8.800 -11.400 -4.600 -8.100 -8.200
-8.800 -13.400 -9.200 -8.200 -8.600 -7.700 -5.900 -7.000 -10.900 -10.900
Вычисления проводить с точностью до 0.001
Вариант номеp - 10
-45.175 -45.362 -47.737 -43.459 -48.223 -40.964 -48.051 -47.890 -42.804 -41.190
-45.427 -52.144 -45.175 -41.777 -46.640 -49.552 -43.150 -46.445 -39.439 -43.039
-44.764 -43.825 -50.183 -45.362 -45.929 -45.852 -48.810 -47.454 -45.057 -45.057
-48.810 -41.595 -42.110 -50.997 -49.036 -41.777 -43.825 -42.263 -46.640 -40.964
-43.991 -41.190 -46.743 -42.678 -44.507 -43.039 -43.909 -47.592 -42.263 -44.573
-47.454 -48.223 -43.648 -44.702 -45.852 -44.224 -41.777 -33.935 -44.885 -45.852
-45.057 -45.703 -44.702 -56.065 -47.890 -45.929 -40.717 -56.065 -45.298 -44.638
-47.890 -41.595 -45.631 -42.408 -38.487 -42.804 -48.600 -39.817 -46.009 -42.263
-44.148 -46.961 -44.885 -52.958 -45.631 -43.991 -48.223 -33.935 -56.065 -44.573
-44.638 -46.850 -44.885 -45.852 -51.513 -56.065 -49.283 -49.552 -44.638 -46.009
Вычисления проводить с точностью до 0.001
Тема 2: «Аппроксимация функций. Метод наименьших квадратов».
Справочный материал
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f(x)
| x | 
| 
| … | 
|
| f(x) | 
| 
| … | 
|
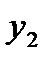
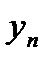
Требуется найти формулу, выражающую данную зависимость аналитически.
Рассмотрим один из наиболее распространенных способов нахождения функции F(x). Предположим, что приближающая функция в точках , ,…, имеет значения 
, 
,…, 
. Воспользовавшись метрикой Евклидова пространства, приходим к требованию, чтобы величина 
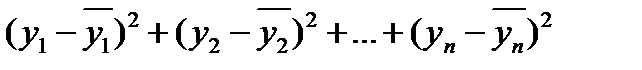была наименьшей.
Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающей функции, зависящей от трех параметров: 
.
Имеем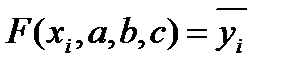 
.
Сумма квадратов разностей соответствующих значений функци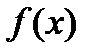й 
и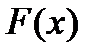 
имеет вид:
. Сумма является функцией 
от трех переменных. Используя необходимое условие экстремума: 
, 
, 
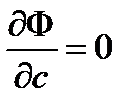получаем систему уравнений
Решив систему относительно параметров a,b,c получаем конкретный вид функции F(x,a,b,c). Изменение количества параметров не приведет к изменению сути самого подхода, а выразится в изменении количества уравнений в системе.
Значения разностей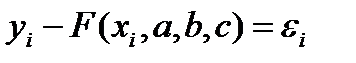 
называют отклонениями измеренных значений,
от вычисленных по формуле. Сумма квадратов отклонений 
в соответствии с принципом наименьших квадратов должна быть наименьшей. Из двух разных приближений одной и той же таблично заданной функции лучшим считается то, для которого 
имеет наименьшее значение.
Нахождение приближающей функции в виде линейной функции.
Ищем приближающую функцию в виде 
Находим частные производные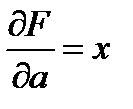 
, 
.
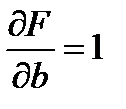Составляем систему вида
Далее имеем: 
Разделим каждое уравнение системы на n, получаем:
Введем обозначения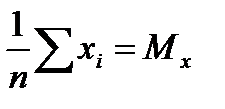 
, 
, 
, 
.
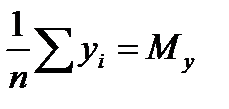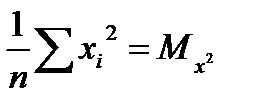Тогда последняя система будет иметь вид:
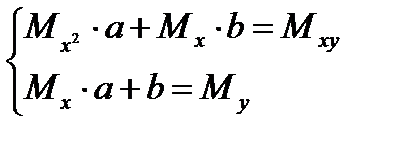или в матричной форме 
Вычислив значения параметров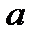 
, 
в соответствии с формулами, получаем конкретные значения и, следовательно, конкретный вид линейной функции.
Нахождение приближающей функции в виде квадратичной функции.
Ищем приближающую функцию в виде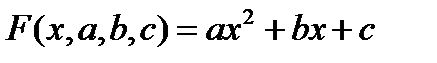 
Находим частные производные 
, 
, 
Составляем систему вида
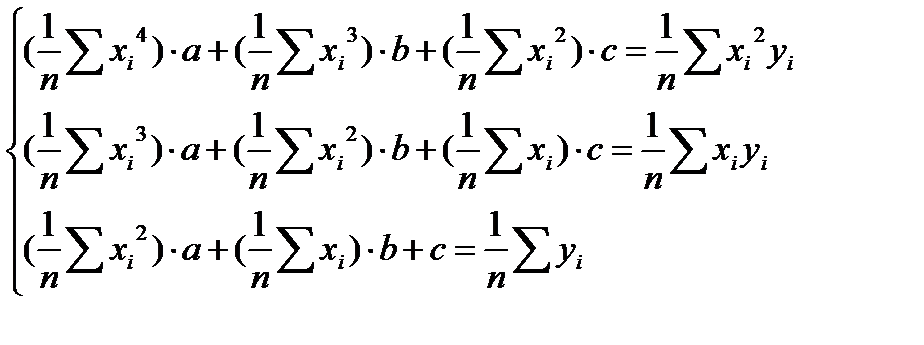
Пример.
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f(x)
| x | 1 | 2 | 3 | 4 |
| f(x) | 2.9 | 5.2 | 6.8 | 9.2 |
а) Требуется найти формулу в виде линейной функции, выражающую данную зависимость аналитически.
Решение.
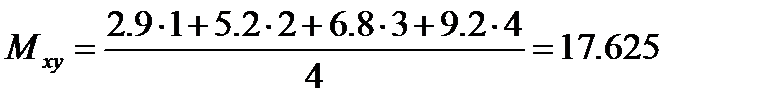
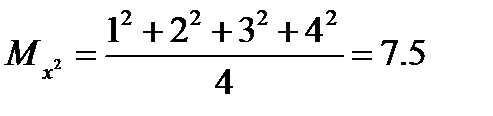
Находим обратную матрицу:
, 
, 
, 
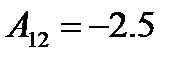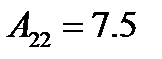
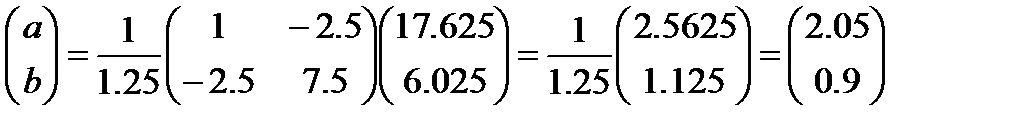. Значит, 
, 
Следовательно, приближающая функция в виде линейной функции имеет вид
Ответ: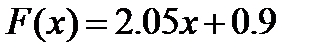 
) Требуется найти формулу в виде квадратичной функции, выражающую данную зависимость аналитически.
Решение.
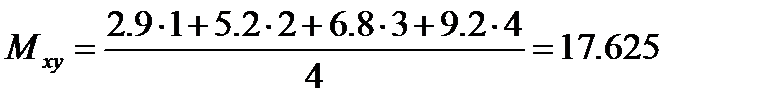
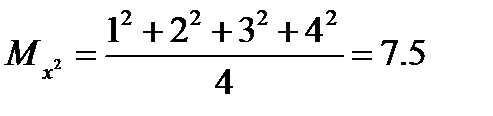
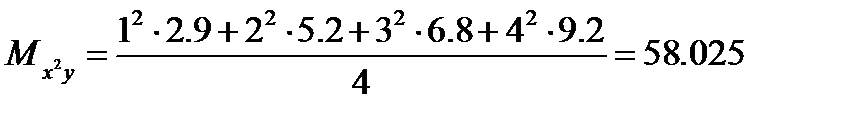
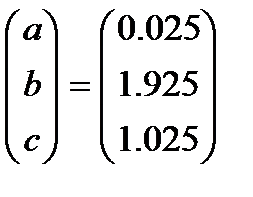
Следовательно, приближающая функция в виде квадратного трехчлена имеет вид 
Ответ:
Определить, какое приближение лучше.
Для этого вычислим сумму квадратов отклонений в первом и во втором случае:
Значения полученных в результате функций поместим в данную таблицу:
| x | 1 | 2 | 3 | 4 |
| f(x) | 2.9 | 5.2 | 6.8 | 9.2 |
|
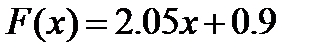
| 2.95 | 5 | 7.05 | 9.1 |
|
| 2.975 | 4.975 | 7.025 | 9.125 |
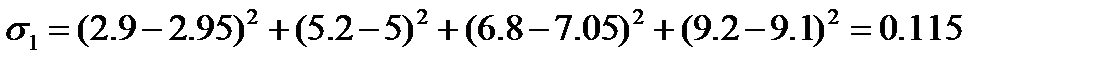
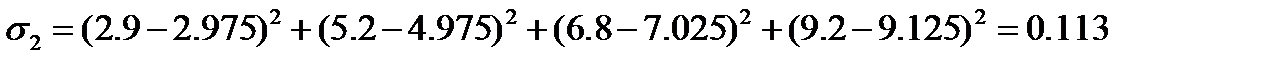
Вывод: для данной функции приближение в виде квадратичной функции лучше.
Задание 2.
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f(x).
а) Требуется найти формулу в виде линейной функции, выражающую данную зависимость аналитически.
б) Требуется найти формулу в виде квадратичной функции, выражающую данную зависимость аналитически.
в) Определить, какое приближение лучше.
| № варианта | Исходные данные | ||||||||
| x | 1.00 | 1.11 | 2.58 | 3.32 | 4.06 | 5.02 | 5.50 | 6.20 | |
| y | 10.01 | 10.15 | 19.07 | 28.47 | 41.15 | 62.50 | 75.25 | 96.32 | |
| x | 0.73 | 1.16 | 1.99 | 2.22 | 4.04 | 5.08 | 5.52 | 6.22 | |
| y | 9.95 | 10.24 | 13.93 | 15.69 | 40.77 | 64.02 | 75.81 | 96.97 | |
| x | 0.05 | 1.64 | 2.28 | 2.80 | 4.10 | 5.10 | 5.54 | 6.24 | |
| y | 11.76 | 11.87 | 16.20 | 21.52 | 41.93 | 64.53 | 76.38 | 97.61 | |
| x | 0.34 | 1.2 | 2.18 | 3.22 | 4.80 | 5.12 | 5.56 | 6.26 | |
| y | 10.65 | 10.32 | 15.36 | 27.01 | 57.12 | 65.04 | 76.94 | 98.26 | |
| x | 0.91 | 1.94 | 2.36 | 3.58 | 4.30 | 5.16 | 5.58 | 6.28 | |
| y | 9.93 | 13.60 | 16.91 | 32.55 | 45.97 | 66.08 | 77.51 | 98.92 | |
| x | 1.20 | 1.57 | 2.80 | 3.32 | 4.68 | 5.18 | 5.60 | 6.30 | |
| y | 10.32 | 11.55 | 21.52 | 28.47 | 54.31 | 66.60 | 78.08 | 99.57 | |
| x | 1.05 | 1.61 | 2.56 | 3.12 | 4.66 | 5.20 | 5.62 | 6.32 | |
| y | 10.06 | 11.73 | 18.86 | 25.60 | 53.85 | 67.12 | 78.65 | 100.23 | |
| x | 1.10 | 1.67 | 2.60 | 3.28 | 4.44 | 5.22 | 5.64 | 6.34 | |
| y | 10.13 | 12.02 | 19.28 | 27.88 | 48.94 | 67.65 | 79.23 | 100.89 | |
| x | 1.35 | 1.97 | 2.16 | 3.42 | 4.34 | 5.28 | 5.66 | 6.36 | |
| y | 10.72 | 13.79 | 15.20 | 29.99 | 46.81 | 68.70 | 79.81 | 101.55 | |
| x | 1.15 | 2.05 | 2.78 | 3.44 | 4.38 | 5.32 | 5.68 | 6.38 | |
| y | 10.22 | 14.36 | 21.29 | 30.30 | 47.65 | 70.31 | 80.39 | 102.21 |