Одним из основных элементов процесса оценки машин является сбор информации, в частности, об их рыночных ценах. Как правило, здесь оценщик сталкивается с таким явлением, когда цены практически идентичных машин, полученные из разных источников, отличаются друг от друга. В этом случае говорят, что собранные оценщиком значения цен являются случайными (или стохастическими) величинами.
На основе собранной информации оценщику в этом случае приходится определять статистические оценки ряда величин, в частности, среднее значение рыночной цены объекта оценки. При малых объемах собранной информации оценщик должен быть уверен в ее качестве. Поэтому уже на стадии предварительной обработки информации он должен провести отсев резко выделяющихся наблюдений в выборке и проверку гипотезы о нормальности распределения. Только после этого возможно применение методов и соотношений, хорошо разработанных для нормального распределения.
Однако на практике оценщик всегда пользуется данными выборки из генеральной совокупности данных. В этом случае некоторые основные свойства случайных величин могут быть описаны более просто по данным выборки с помощью оценок параметров их функций распределения, называемых также статистиками. Подробно о математической статистике можно говорить долго, так достаточно много способов статистической обработки.
Важнейшими из статистических величин, являются: среднее (среднее арифметическое) значение выборки (оценка математического ожидания), которую рассчитывают по формуле 6.
, формула 6
Где xi - значение одного из параметров выборки
Характеристика разброса наблюдаемых величин - дисперсия выборки (оценка дисперсии s2) рассчитывается по формуле 7
, формула 7
Где n - число наблюдеий в генгеральной совокупности
Среднее квадратическое (стандартное) отклонение выборки рассчитывают по формуле 8.
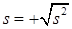. формула 8
Стандартное отклонение s - мера разброса случайной величины вокруг среднего значения, имеющая размерность, совпадающую с размерностью случайной величины, что полезно при определении погрешностей расчетных оценок.
К характеристикам разброса данных относится также коэффициент вариации (ν) выборки. (формула 9)
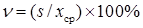, формула 9
Значение n выражает среднее квадратическое отклонение s в процентах от среднего x ср совокупности данных и поэтому может быть использовано для оценки их точности. Выборка является точной если коэффициент вариации менее 33%.
Собрать данные обо всех значениях xi из генеральной совокупности практически невозможно. Поэтому реально оценщик довольствуется выборкой, а методы математической статистики помогают ему по известным свойствам объектов из выборки судить о свойствах всей генеральной совокупности.
Проведем дисперсионный анализ данных, расчитая основные статистические характеристики.
Используя данные генеральной совокупности и выше приведенные формулы для расчёта статистических величин получаем:
Среднее значение составило - 110330 руб.
Среднее квадратическое отклонение составило 10 781 руб.
Коэффициент определяющий точность выборки (коэффициент вариации) составил 10%, что удовлетворяет точности нормального распределения (точность должна быть менее 33%)