Физика – наука экспериментальная. Это значит, что физические законы устанавливают и проверяют через накопление и сравнение экспериментальных данных. Но результаты, которые получают при проведении любого физического эксперимента, всегда содержат некоторые погрешности, так как практически невозможно провести измерения с абсолютной точностью. Возможные погрешности имеют большое значение при сравнении результатов эксперимента с теоретическими формулами, поэтому необходимо научить студентов обрабатывать результаты измерений.
Поэтому целесообразным является проведение фронтальной лабораторной работы по теме «Освоение методов проведения измерений и расчета их погрешностей» для более качественного усвоения студентами знаний по теории погрешностей и умений применять эти знания в практической деятельности. Целью данной работы является ознакомление с методами оценки результатов измерений и расчета погрешностей. В качестве оборудования используется установка для определения удельного сопротивления проволоки (рис. 1), штангенциркуль, микрометр, рулетка. Материалом изучения является следующее: прямые и косвенные измерения, определение погрешностей, приближенные вычисления, измерение линейных величин, простейшие электрические измерения.
Рабочая формула для вычисления удельного сопротивления материала проволоки:
.
Чтобы определить ρ, необходимо измерить электрическое сопротивление R (через силу тока I и напряжение U), длину отрезка l и площадь его сечения S (через диаметр d).
Напряжение U, силу тока I, длину l отрезка проволоки и ее диаметр d мы измеряем соответствующими приборами с определенной точностью. Когда мы говорим, что вольтметр показывает 1 В, мы, конечно, имеем в виду, что измеряемое напряжение лишь приблизительно равно 1 В. Истинное значение напряжения лежит в некотором интервале
|
|
Uизм – ∆U ≤ U ≤ Uизм + ∆U, или U = Ū ± ∆U,
где Uизм – измеренное напряжение; в нашем примере Uизм = 1 В. Значит, результат измерения есть то деление на шкале вольтметра, против или вблизи которого установилась стрелка, ∆U – погрешность измерения напряжения данным вольтметром, она определяется классом точности прибора. Отметим, что ∆U определяется «ценой» деления шкалы вольтметра. Это же относится и к измеряемой силе тока I:
I = Ī ± ∆I.
Диаметр d проволоки можно измерить штангенциркулем или микрометром. Если диаметр проволоки измерить штангенциркулем в разных местах, то, скорее всего, окажется, что результат везде одинаков. Штангенциркуль не «почувствует», что толщина проволоки не одинакова по всей длине. В этом случае точность измерения штангенциркулем и определяет погрешность измерения диаметра. Микрометр – более чувствительный и более точный прибор, чем штангенциркуль. Если измерить диаметр проволоки в различных местах микрометром, то можно получить серию результатов d1, d2, …, dn. В этом случае погрешность определяется уже и характером самой величины d. Тоеть, истинное значение диаметра лежит в интервале
d = 
± ∆ d.
Это же относится и к измеряемой длине проволоки l:
l = 
± ∆ l.
Отсюда приходим к искомому результату
ρ =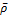 
± ∆ ρ = 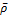(1 ± 
).
где относительная погрешность
Студенты работают по следующему плану:
|
|
1. Определение с помощью штангенциркуля диаметра d проволоки по всей длине в 10 – 12 точках. Определение среднего значения диаметра
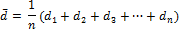
и запись резутата в виде
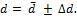
Вычисление погрешности измерений 
и относительной погрешности 
.
2. Повторение измерения диаметра проволоки с помощью микрометра. Определение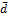 
и . Результаты измерений заносятся в специальную таблицу. Вычисление 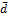и по формулам
,
и сравнение полученных результатов.
3. Определение экспериментально зависимости сопротивления R проволоки от ее длины l. Измерения рекомендуется проводить для десяти значений длины l от l ≈ 0,3 l 0 до l = l 0, где l 0 – полная длина проволоки.
4. Определение погрешностей ΔU и ΔI по классу точности вольтметра и амперметра.
5. Нанесение экспериментальных точек на координатную плоскость, откладывая по оси Х величину , а по оси Y – соответствующее ей сопротивление 
. Каждую экспериментальную точку следует изображать с указанием погрешностей Δ l и ΔR. При этом необходимо убедится в том, что в пределах точности измерений экспериментальные точки ложатся на прямую.
Презентация