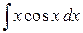ВНИМАНИЕ. Две пары и две темы. Читаем, небольшой конспект с формулами и самостоятельную работу
Тема: Метод подстановки в неопределенном интеграле
Метод подстановки в неопределенный интеграл
Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно свести к одному или нескольким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (замены переменной).
Заметим, что все способы интегрирования имеют целью свести данный интеграл к табличному с помощью тех или иных искусственных приемов.
Способ подстановки заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, на который всегда можно умножить и разделить подынтегральное выражение).
Например, в интеграле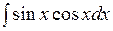 
удобно произвести замену 
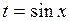, так как оставшаяся часть подынтегрального выражения равна 
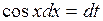. Тогда перепишем данный интеграл в виде 
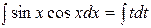. Полученный интеграл является табличным; он находится по формуле 1: 
.
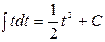Далее, производя обратную замену 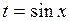, получим ответ: 
.
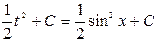Решение этого примера можно кратко оформить так:
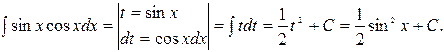
Напомним, что если при интегрировании одной и той же функции разными способами получили различные результаты, то необходимо показать, что они отличаются на постоянную величину.
Так, рассмотренный выше пример можно решить иначе, если применить формулу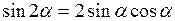 
.
Тогда получим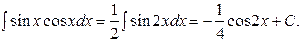 
Результат по виду отличается от найденного ранее; однако, преобразуя первый результат, имеем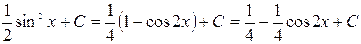 
.
Отсюда видно, что разность функций равна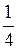 
, т.е. постоянному числу.
Естественно, возникает вопрос: как правильно выбрать подстановку? Это достигается практикой в интегрировании. Все же можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.
Правило интегрирования способом подстановки состоит в следующем:
1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
4. Производят замену под интегралом.
5. Находят полученный интеграл.
6. В результате производят обратную замену, то есть переходят к старой переменной. Результат полезно проверить дифференцированием.
Рассмотрите примеры и вычислите по образцу.
Образец
= 
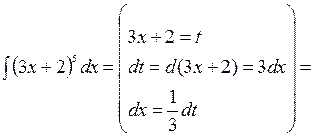
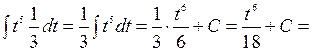
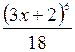
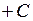
Вычислить: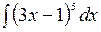 
Образец
= 
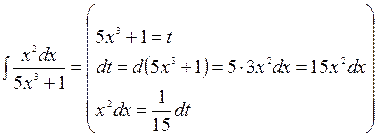
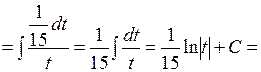
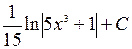
Вычислить: 
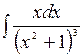
Образец
= 
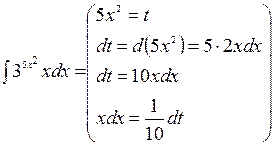
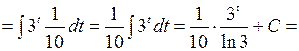
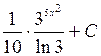
Вычислить: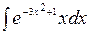 
Образец
=
= 
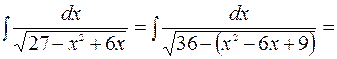
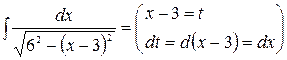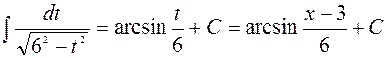
Вычислить: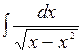 
 |
Образец
= 
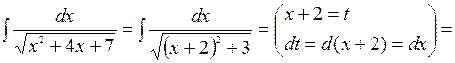
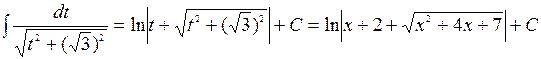
Вычислить: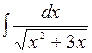 
Образец
= 
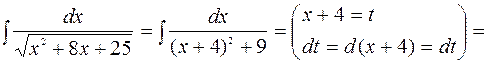
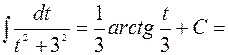
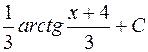
Вычислить: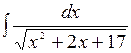 
Интегрирование по частям
Некоторые виды интегралов, вычисляемых по частям
Если производные функци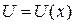й 
и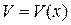 
непрерывны, то справедлива формула:
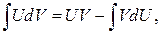(3)
называемая формулой интегрирования по частям.
В качестве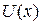 
обычно выбирают функцию, которая упрощается при дифференцировании.
Некоторые стандартные случаи функций, интегрируемых по частям, указаны в таблице 1. Там же дается способ выбора множителе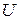й 
и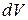 
.
Таблица 1
| Вид интеграла |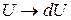 
| 
|
| 
| 
|
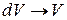
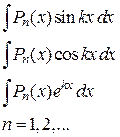
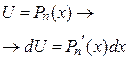
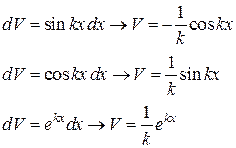
| Вид интеграла |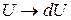
|
|
| 
| 
|
| 
| |
| 
| |
| 
| |
| 
| |
|
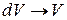
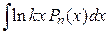
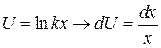
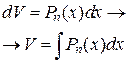
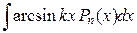
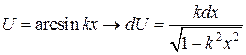
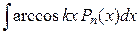
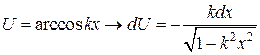
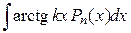
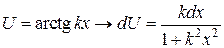
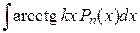
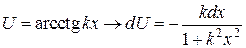
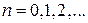
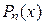— многочлен от 
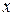степени 
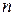, т. е. 
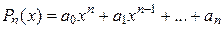, где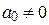 
.
Пример 2. Проинтегрировать по частям.
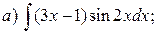
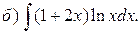
Решение.
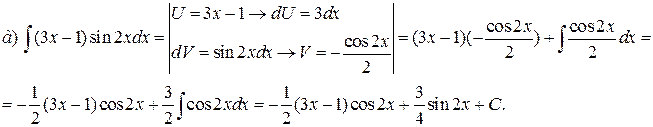
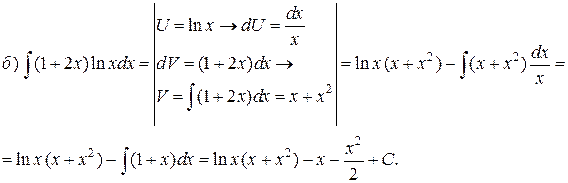
Задание. Найти интеграл интегрированием по частям:
1. 
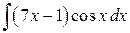
2. 
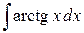
3. 
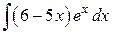
4. 
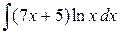
5. 