Геометрические приложения

Лекция 21 Приложения определенного интеграла (2ч)

Содержание лекции: Геометрические и физические приложения определенного интеграла: вычисление площадей плоских фигур, объемов тел вращения, длины дуги, массы прямолинейного стержня, работы силы.

 

Геометрические приложения

 

а) Площадь фигуры

Как уже отмечалось в лекции 19, численно равен площади криволинейной трапеции, ограниченной кривой у = f (x), прямыми х = а, х = b и отрезком [ a, b ] оси ОХ. При этом если f (x) £ 0 на [ a, b ], то интеграл следует взять со знаком минус.

Если же на заданном отрезке функция у = f (x) меняет знак, то для вычисления площади фигуры, заключенной между графиком этой функции и осью ОХ, следует разбить отрезок на части, на каждой из которых функция сохраняет знак, и найти площадь каждой части фигуры. Искомая площадь в этом случае есть алгебраическая сумма интегралов по этим отрезкам, причем интегралы, соответствующие отрицательным значения функции, взяты в этой сумме со знаком «минус».

Если фигура ограничена двумя кривыми у = f ₁(x) и у = f ₂(x), f ₁(x)£ f ₂(x), то, как следует из рис.9, ее площадь равна разности площадей криволинейных трапеций а ВС b и а АD b, каждая из которых численно равна интегралу. Значит,

.

 

Заметим, что площадь фигуры, изображенной на рисунке 10,а находятся по такой же формуле: S = (докажите это!). Подумайте, как вычислить площадь фигуры, изображенной на рисунке 10,б?

 

 

Мы вели речь только о криволинейных трапециях, прилежащих к оси ОХ. Но аналогичные формулы справедливы и для фигур, прилежащих к оси ОУ. Например, площадь фигуры, изображенной на рисунке 11, находится по формуле

S = .

Пусть линия y = f (x), ограничивающая криволинейную трапецию, может быть задана параметрическими уравнениями , t Î [a, b], причем j(a)= а, j(b) = b, т.е. у = . Тогда площадьэтой криволинейной трапеции равна

.

б) Длина дуги кривой

Пусть дана кривая у = f (x). Рассмотрим дугу этой кривой, соответствующую изменению х на отрезке [ a, b ]. Найдем длину этой дуги. Для этого разобьем дугу АВ на п частей точками А = М₀,М₁, М_2, ..., М _п = В (рис.14), соответствующими точкам х ₁, х ₂,..., х_п Î [ a, b ].

 

 

 

 

Обозначим D l_i длину дуги , тогда l = . Если длины дуг D l_i достаточно малы, то их можно считать приближенно равными длинам соответствующих отрезков , соединяющих точки М _{i -1, M i} . Эти точки имеют координаты М _{i -1}(х_{i -1, f} (x_{i -1})), M _i (х_i, f (x_i)). Тогда длины отрезков равны соответственно

.

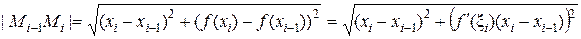Здесь использована формула Лагранжа. Положим х_i – x_{i -1} =D х_i, получим

Тогда l = , откуда

l = .

Таким образом, длина дуги кривой у = f (x), соответствующей изменению х на отрезке [ a, b ], находится по формуле

l = , (1)

Если кривая задана параметрически , t Î[a, b], т.е. y (t) = f (x (t)), то из формулы (1) получим:

l = .

Значит, если кривая задана параметрически , то длина дуги этой кривой, соответствующей изменению t Î[a, b], находится по формуле

в) Объем тела вращения.

Рис.15

Рассмотрим криволинейную трапецию а АВ b, ограниченную линией у = f (x), прямыми х = а, х = b и отрезком [ a, b ] оси ОХ (рис.15). Пусть эта трапеция вращается вокруг оси ОХ, в результате получится тело вращения. Можно доказать, что объем этого тела будет равен

Аналогично можно вывести формулу объема тела, полученного вращением вокруг оси ОУ криволинейной трапеции, ограниченной графиком функции х = j(у), прямыми y = c, y = d и отрезком [ c, d ] оси ОУ (рис.15):