Тождественные преобразования выражений и методика обучения учащихся их выполнению
Исполнитель:
Студентка Стародубова А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент Лебедева М.Т.
Гомель 2007
Содержание
Введение
1 Основные типы преобразований и этапы их изучения. Этапы освоения применения преобразований
2 Особенности организации системы заданий при изучении тождественных преобразований
Заключение
Литература
Введение
Простейшие преобразования выражений и формул, опирающиеся на свойства арифметических операций, производятся в начальной школе и 5 и 6 классах. Формирование умений и навыков выполнения преобразований происходит в курсе алгебры. Это связано как с резким увеличением числа и разнообразия совершаемых преобразований, так и с усложнением деятельности по их обоснованию и выяснению условий применимости, с выделением и изучением обобщенных понятий тождества, тождественного преобразования, равносильного преобразования.
Основные типы преобразований и этапы их изучения. Этапы освоения применения преобразований
1. Начала алгебры
Используется нерасчлененная система преобразований, представленная правилами выполнения действий над одной или обеими частями формулы. Цель – достичь беглости в выполнении заданий на решение простейших уравнений, упрощение формул, задающих функции, в рациональном проведении вычислений с опорой на свойства действий.
Типичные примеры:
Решить уравнения:
а)  ; б)
; б)  ; в)
; в) 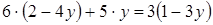 .
.
Тождественное преобразование (а); равносильное и тождественное (б).
2. Формирование навыков применения конкретных видов преобразований
Выводы: формулы сокращенного умножения; преобразования, связанные с возведением в степень; преобразования, связанные с различными классами элементарных функций.
Организация целостной системы преобразований (синтез)
Цель – формирование гибкого и мощного аппарата, пригодного для использования в решении разнообразных учебных заданий. Переход к этому этапу осуществляется при итоговом повторении курса в ходе осмысления уже известного материала усвоенного по частям, по отдельным типам преобразований к ранее изученным видам добавляют преобразования тригонометрических выражений. Все эти преобразования можно назвать “алгебраическими” к “аналитическим” преобразованиям можно отнести те из них, в основе которых лежат правила дифференцирования и интегрирования и преобразования выражений, содержащих предельные переходы. Отличие этого типа – в характере множества, которое пробегают переменные в тождествах (определенные множества функций).
Изучаемые тождества подразделяются на два класса:
I – тождества сокращенного умножения, справедливые в  коммутативном кольце и тождества
коммутативном кольце и тождества
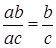 ,
,  ,
,
справедливого в  поле.
поле.
II – тождества, связывающие арифметические операции и основные элементарные функции.
Особенности организации системы заданий при изучении тождественных преобразований
Основной принцип организации  системы заданий – предъявление их от простого к сложному.
системы заданий – предъявление их от простого к сложному.
Цикл упражнений – соединение в последовательности упражнений нескольких аспектов изучения и приемов расположения материала. При изучении тождественных преобразований цикл упражнений связан с изучением одного тождества, вокруг которого группируются другие тождества, находящиеся с ним в естественной связи. В состав цикла наряду с исполнительными входят задания, требующие распознавания применимости рассматриваемого тождества. Изучаемое тождество применяется для проведения вычислений на различных числовых областях. Задания в каждом цикле разбиты на две группы. К первой относятся задания, выполняемые при первоначальном знакомстве с тождеством. Они служат учебным материалом для нескольких идущих подряд уроков, объединенных одной темой.
Вторая группа упражнений связывает изучаемое тождество с различными приложениями. Эта группа не образует композиционного единства – упражнения здесь разбросаны по различным темам.
Описанные структуры цикла относятся к этапу формирования навыков применения конкретных преобразований.
На этапе синтеза циклы изменяются, происходит объединение групп заданий в сторону усложнения и слияния циклов, относящихся к различным тождествам, что способствует повышению роли действий по распознаванию применимости того или иного тождества.
Пример.
Цикл заданий для тождества:
 .
.
I группа заданий:
а) представить в виде произведения:
 .
.
б) Проверить верность равенства:
 .
.
в) Раскрыть скобки в выражении:
 .
.
г) Вычислить:
 .
.
д) Разложить на множители:
 .
.
е) упростить выражение:
 .
.
Ученики только что ознакомились с формулировкой тождества, его записью в виде тождества, доказательством.
Задание а) связано с фиксированием структуры изучаемого тождества, с установлением связи с числовыми множествами (сопоставление знаковых структур тождества и преобразуемого выражения; замещение буквы числом в тождестве). В последнем примере еще предстоит выполнить приведение его к изучаемому виду. В следующих примерах (д и ж) происходит усложнение, вызванное прикладной ролью тождества и усложнением знаковой структуры.
Задания типа б) направлены на формирование навыков замены  на
на  . Аналогична роль задания в).
. Аналогична роль задания в).
Примеры типа г), в которых требуется выбрать одно из направлений преобразования, завершает развитие этой идеи.
Задания I группы ориентированы на усвоение структуры тождества, операции замещения в простейших, принципиально наиболее важных случаях, и представления об обратимости преобразований, осуществляемых тождеством. Очень важное значение имеет также обогащение языковых средств, показывающих различные аспекты тождества. Представление об этих аспектах дают тексты заданий.
II группа заданий.
ж) Используя тождество  при
при  , разложить на множители многочлен
, разложить на множители многочлен  .
.
з) Исключить иррациональность в знаменателе дроби  .
.
и) Доказать что если  - нечетное число, то
- нечетное число, то  делится на 4.
делится на 4.
к) Функция задана аналитическим выражением
 .
.
Избавиться от знака модуля, рассмотрев два случая:  ,
,  .
.
л) Решить уравнение  .
.
Эти задания направлены на возможно более полное использование и учет специфики именно данного тождества, предполагают сформированность навыков использования изучаемого тождества для разности квадратов. Цель – углубить понимание тождества за счет рассмотрения разнообразных приложений его в различных ситуациях, в сочетании с использованием материала, относящегося к другим темам курса математики.







или  .
.
Особенности циклов заданий, связанных с тождествами для элементарных функций:
1) они изучаются на базе функционального материала;
2) появляются позже тождества первой группы и изучаются с использованием уже сформированных навыков проведения тождественных преобразований.
В первую группу заданий цикла должны войти задания на установление связи этих новых числовых областей с исходной областью рациональных чисел.
Пример.
Вычислить:


 ;
;


 ;
;


 .
.


 .
.
Цель таких заданий – освоение особенностей записей, включающих символы новых операций и функций, и в развитии навыков математической речи.
Значительная часть использования тождественных преобразований, связанных с элементарными функциями, приходится на решение иррациональных и транцендетных уравнений. Последовательность шагов:
а) найти функцию φ, для которой данное уравнение f(x)=0 представимо в виде:
F(φ(x))=0;
б) произвести подстановку y=φ(x) и решить уравнение
F(y)=0;
в) решить каждое из уравнений φ(x)=yk, где yk-множество корней уравнения F(y)=0.
При использовании описанного способа зачастую шаг б) выполняется в неявном виде, без введения обозначения для φ(x). Кроме того, ученики зачастую предпочитают из различных путей, ведущих к нахождению ответа, выбирать тот, который быстрее и проще приводит к алгебраическому уравнению.
Пример. Решить уравнение 4x-3*2=0.
1)  ;
;
2)(22)x-3*2x=0 (шаг а)
(2x)2-3*2x=0; 2x (2x -3)=0; 2x-3=0. (шаг б)
Пример. Решить уравнение:
а) 22x-3*2x+2=0;
б) 22x-3*2x-4=0;
в) 22x-3*2x+1=0.
(Предложить для самостоятельного решения.)
Классификация заданий в циклах, относящихся к решению транцендетных уравнений, включающих показательную функцию:
1) уравнения, сводящиеся к уравнениям вида аx=y0 и имеющие простой, общий по форме ответ:
x=logay0;
2) уравнения, сводящиеся к уравнениям вида аx= аk, где k- целое число, или аx=b, где b≤0.
3) уравнения, сводящиеся к уравнениям вида аx=y0, и требующие явного анализа формы, в которой явно записано число y0.
Большую пользу приносят задания, в которых тождественные преобразования используются для построения графиков при упрощении формул, задающих функции.
Пример.
а) Построить график функции y=  ;
;
б) Решить уравнение lgx+lg(x-3)=1
в) на каком множестве формула lg(x-5)+ lg(x+5)= lg(x2-25) является тождеством?
Использование тождественных преобразований в вычислениях.(ж. Математика в школе, №4, 1983, стр.45)
Задача№1. Функция задана формулой y=0,3x2+4,64x-6. Найдите значения функции при x=1,2
y(1,2)=0,3*1,22+4,64*1,2-6=1,2(0,3*1,2+4,64)-6=1,2(0,36+4,64)-6=1,2*5-6=0.
Задача№2. Вычислите длину катета прямоугольного треугольника, если длина его гипотенузы равна 3,6см, а другого катета- 2,16см.

Задача№3. Какова площадь участка прямоугольной формы, имеющего размеры а) 0,64м и 6,25м; б) 99,8м и 2,6м?
а)0,64*6,25=0,82*2,52=(0,8*2,5)2;
б)99,8*2,6=(100-0,2)2,6=100*2,6-0,2*2,6=260-0,52.
Эти примеры позволяют выявить практическое применение тождественных преобразований. Учащегося следует ознакомить с условиями выполнимости преобразования.(см. схемы).
|

 -
-
изображение многочлена, где в круглые контуры вписывается любой многочлен.(схема 1)

 -
-
условие выполнимости преобразования произведения одночлена и приведено выражение, допускающее преобразование в разность квадратов. (схема 2)

 -
-
здесь штриховки означают равные одночлены и приведено выражение допускающее преобразование в разность квадратов.(схема 3)

|
|

 -
-
выражение, допускающее вынесение общего множителя.
Сформировать умения учащихся по выявлению условий можно с помощью следующих примеров:
Какие из следующих выражений могут быть преобразованы вынесением общего множителя за скобки:
1) 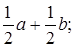
2) 
3) 0,7а2+0,2b2;
4) 
5) 6,3*0,4+3,4*6,3;
6) 2x2+3x2+5y2;
7) 0,21+0,22+0,23.
Большинство вычислений на практике не удовлетворяют условиям выполнимости, поэтому учащимся необходимы навыки приведения их к виду, допускающему вычисления преобразований. В этом случае целесообразны такие задания:
при изучении вынесения общего множителя за скобки:
данное выражение, если это возможно, преобразуйте в выражение, которое изображается схемой 4:
1) 15a+121b;
2) 26m-2,6n;
3) 7xy+14y2;
4) 2а*а2*а2;
5) 2n4+3n6+n9;
6) x3+x2+x;
7) (a+1)2;
8) 15ab2+5a2b;
9) (ac)2+2ac;
10) 12,4*  -1,24*0,7;
-1,24*0,7;
11) 4,9*3,5+1,7*10,5;
12) 10,82-108;
13) 
14) 5*22+7*23-11*24;
15) 2*34-3*24+6;
16) 62+82;
17) 62-82;
18) 3,2/0,7-1,8* 
19) 11*27-8*13.
При формировании понятия «тождественное преобразование» следует помнить, что это означает не только то, что данное и полученное выражение в результате преобразования принимают равные значения при любых значениях входящих в него букв, но и то, что при тождественном преобразовании мы переходим от выражения, определяющего один способ вычисления, к выражению, определяющему другой способ вычисления того же значения.

 схема 5
схема 5
Можно схему 5(правило преобразования произведения одночлена и многочлена) проиллюстрировать на примерах
0,5a(b+c) или 3,8(0,7+  ).
).
Упражнения для изучения вынесения общего множителя за скобки:
Вычислите значение выражения:
а) 4,59*0,25+1,27*0,25+2,3-0,25;
б) a+bc при a=0,96; b=4,8; c=9,8.
в) a(a+c)-c(a+b) при a=1,4; b=2,8; c=5,2.
Проиллюстрируем на примерах формирование умений и навыков в вычислениях и тождественных преобразованиях.(ж. Математика в школе, №5, 1984, стр.30)
1) умения и навыки быстрее усваиваются и дольше сохраняются, если их формирование происходит на сознательной основе (дидактический принцип сознательности).
Пример:
1) Можно сформулировать правило сложения дробей с одинаковыми знаменателями или предварительно на конкретных примерах рассмотреть суть сложения одинаковых долей.
2) При разложении на множители вынесением общего множителя за скобки важно увидеть этот общий множитель и затем применить распределительный закон. При выполнении первых упражнений полезно каждое слагаемое многочлене записать в виде произведения, один из множителей которого- общий для всех слагаемых:
3a3-15a2b+5ab2= a3a2-a15ab+a5b2.
Особенно полезно так поступать, когда за скобки выносится один из одночленов многочлена:

II. Первый этап формирования навыка – овладение умением (упражнения выполняются с подробными объяснениями и записями)

(первым решается вопрос о знаке)
Второй этап – этап автоматизации умения путем исключения некоторых промежуточных операций

III. Прочность навыков достигается решением разнообразных как по содержанию, так и по форме, примеров.