Указания к выполнению задания

Расчет бункера для сыпучих материалов

(расчетно-графическая работа)

Цель работы

Исследование распределения усилий по высоте в стенках бункера для сыпучих материалов, расчет бункера на прочность.

Общие положения, расчетные формулы

Динамические и статические свойства сыпучих материалов существенно отличаются от свойств сплошных сред. Так, давление в жидкости , где – плотность жидкости; g – ускорение силы тяжести; h – высота столба жидкости (расстояние от поверхности жидкости в направлении действия силы тяжести и во всех направлениях одинаково). В сыпучих материалах вес столба материала частично удерживается трением материала о стенки сосуда (бункера) и сцеплением частиц между собой. В неподвижном слое сыпучего материала трение материала о стенки сосуда характеризуется коэффициентом внешнего трения покоя и углом внешнего трения покоя , которые связаны между собой как , а при движении сыпучего материала – коэффициентом внешнего трения движения и углом внешнего трения движения . Аналогично 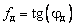. Сцепление частиц между собой в сыпучем материале характеризуется эффективным внутренним коэффициентом трения и внутренним углом трения , при этом . Кроме того, давление сыпучего материала на боковые вертикальные стенки не равно давлению по вертикали :

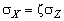, (5.1)

где – коэффициент бокового давления:

. (5.2)

Для цилиндрических и призматических сосудов с вертикальными стенками вертикальное давление неподвижного слоя сыпучего материала

, (5.3)

где z – высота слоя; – насыпная плотность материала; R – гидравлический радиус сосуда. Для цилиндрических сосудов диаметром D 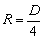, для призматических прямоугольных сосудов с размерами в плане имеем: .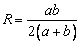

Для конусных частей сосудов, если насыпная плотность мало изменяется от вертикального давления ():

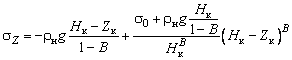, (5.4)

где – полная высота конуса; – координата от верхней точки (основания) конуса; 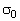– вертикальное давление в верхней точке конуса (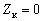) от вышележащих слоев,

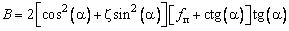, (5.5)

здесь – угол наклона образующей конуса к горизонтали.

Давление сыпучего материала на вертикальные боковые

стенки

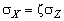, (5.6а)

давление на наклонные стенки:

. (5.6б)

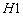Схема бункера приведена на рис. 2, где – диаметр бункера; – высота выше точки подвеса; – высота цилиндрической части; – высота конической части; – текущая координата цилиндрической части; – текущая координата конической части.

Рис. 2. Схема цилиндроконического бункера

Стенки бункера испытывают напряжения: отрывные, действующие вдоль образующей, , и распирающие, действующие по касательной к окружности стенки, , где – отрывные силы, действующие на единицу длины окружности; – распирающие силы, действующие на единицу длины образующей; – толщина стенки бункера. Эквивалентные напряжения в стенке бункера по четвертой теории прочности . Так как отрывные и распирающие силы отличаются от соответствующих напряжений только постоянным множителем, то эффективному напряжению соответствует эффективное усилие

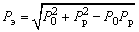. (5.7)

Для конической части бункера отрывные силы:

, (5.8)

где – коэффициент динамичности, зависящий от условий работы; r – радиус конуса на расстоянии : 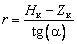, M – масса материала в бункере ниже координаты , если эта координата ниже опоры бункера. Высота конуса . Для конической части бункера: , для цилиндрической части . Насыпная плотность: , где – плотность материала, – его порозность; – влажность материала.

Распирающие силы, действующие на единицу длины образующей

, (5.9)

здесь 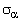– давление на стенку бункера. Для цилиндрической части бункера и 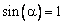, , (см. выражение (5.6)).

Если опора бункера расположена выше рассматриваемого сечения, то силы P0 отрицательны, так как они будут сжимать стенку, а массу материала M следует брать выше рассматриваемого сечения.

Расчетная толщина стенки бункера определяется из условия: 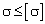, где – напряжение в стенке бункера; – допускаемое напряжение материала стенки. Исполнительная толщина стенки: , где с – поправка на абразивный износ, которую можно принять мм, – поправка на округление – исполнительная толщина стенки округляется в большую сторону до ближайшей стандартной толщины листа.

Задание

1. Построить зависимость изменения вертикального давления , распирающего удельного усилия , отрывного удельного усилия и эффективного усилия по высоте бункера в цилиндрической и конической частях.

2. Определить необходимую толщину стенки цилиндрической и конической частей бункера. Материал стенки – сталь Ст 3, допускаемое напряжение которой МПа.

Указания к выполнению задания

1. Схему бункера с указанием размеров начертить от руки на листе бумаги формата А4 или с помощью персонального компьютера (ПК) в среде AutoCad, «Компас» или др.

2. Толщину стенки определять по максимальному эффективному усилию.

3. В пояснительной записке привести расчетные формулы с пояснениями и графики, выполненные в среде Mathcad.

Контрольные вопросы

1. Справедлив ли закон Паскаля для сыпучих материалов?

2. От чего зависит вертикальная составляющая давления в сыпучих материалах?

3. От чего зависит горизонтальная составляющая давления в сыпучих материалах?

Варианты заданий

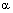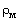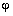Вариант	D, м	H1, м	H2, м	, град	, кг/м3		, град	, град	KD
	2,0				2 800	0,35			1,3
	2,0				2 700	0,4			1,3
	2,5	1,5			2 500	0,45			1,3
	1,5	0,5			2 200	0,35			1,3
	2,0	1,0			2 600	0,45			1,5
	2,5	1,0			2 400	0,40			1,5
	3,5	1,0			2 500	0,50			1,5
	4,0	1,5			2 300	0,30			1,7
	3,5	1,5			2 400	0,35			1,7
	3,0	1,0			2 600	0,40			1,7
	2,5	1,0			2 700	0,50			1,5
	2,0	1,0			2 800	0,55			1,3
	1,5	0,5			2 900	0,45			1,3
	4,0	1,5			2 200	0,40			1,5
	3,0	2,0			2 300	0,35			1,7
	2,0	1,0			2 400	0,30			1,5