Лекция 3
Прямая в 
Векторное уравнение прямой  в пространстве
в пространстве  имеет вид:
имеет вид:
 ,
,  ,
, 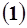

 
 
 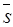 
 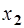
 
| где  произвольный (текущий) вектор прямой
произвольный (текущий) вектор прямой  , ,  базисный
(направляющий) вектор прямой базисный
(направляющий) вектор прямой  . Вектор . Вектор  параллелен прямой параллелен прямой  , ,
 вектор сдвига, его конечная точка вектор сдвига, его конечная точка  принадлежит прямой принадлежит прямой  ; ;  некоторое число. Если
переменная некоторое число. Если
переменная 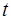 пробегает весь интервал пробегает весь интервал 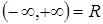 , то точка , то точка  - конец вектора - конец вектора  пробегает всю прямую пробегает всю прямую  . Таким образом, уравнение . Таким образом, уравнение
|
прямой  полностью определяется заданием базисного вектора
полностью определяется заданием базисного вектора 
 и вектора сдвига
и вектора сдвига 
 .
.
Переходя в равенстве 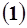 к координатам, получим параметрические уравнения прямой
к координатам, получим параметрические уравнения прямой  :
:
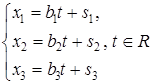

Плоскость в 

 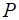
  
 
| При решении задач на составление уравнения плоскости  рекомендуется пользоваться планом:
1) из условия задачи определим координаты какой - нибудь точки рекомендуется пользоваться планом:
1) из условия задачи определим координаты какой - нибудь точки
 , принадлежащей плоскости , принадлежащей плоскости  . .
|
 введем текущую (произвольную) точку
введем текущую (произвольную) точку  плоскости
плоскости  и вычислим текущий вектор
и вычислим текущий вектор  ,
, 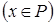 . Далее возможен один из следующих случаев:
. Далее возможен один из следующих случаев:
1 случай: из условия задачи нашли вектор  перпендикулярный плоскости
перпендикулярный плоскости  (
( , такой вектор
, такой вектор  называется нормалью плоскости
называется нормалью плоскости  ). В этом случае векторное уравнение плоскости
). В этом случае векторное уравнение плоскости  будет иметь вид (условие перпендикулярности двух векторов
будет иметь вид (условие перпендикулярности двух векторов 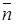 и
и  :
:


переходим в  к координатам, получим
к координатам, получим


- уравнение плоскости  , проходящей через точку
, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
2 случай из условия задачи мы нашли два вектора  и
и 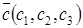 параллельных плоскости
параллельных плоскости  , но не параллельных между собой (такие векторы
, но не параллельных между собой (такие векторы  и
и  называются также базисными векторами плоскости
называются также базисными векторами плоскости  ). В данном случае уравнение плоскости
). В данном случае уравнение плоскости  будет иметь вид (условие линейной зависимости трех векторов
будет иметь вид (условие линейной зависимости трех векторов  ,
,  и
и  ):
):


или в координатной форме:


- уравнение плоскости  , проходящей через точку
, проходящей через точку  параллельно двум базисным векторам
параллельно двум базисным векторам  и
и  .
.
Если раскрыть скобки в уравнении  или определитель в уравнении
или определитель в уравнении  и упростить, то получится общее уравнение плоскости
и упростить, то получится общее уравнение плоскости 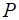 :
:


Геометрический смысл чисел A,B,C состоит в том, что вектор  будет перпендикулярен плоскости.
будет перпендикулярен плоскости.
Взаимное расположение двух плоскостей
Пусть относительно общей декартовой системы координат заданы две плоскости a:  и b:
и b:  .
.
1.  . плоскости a и b пересекаются.
. плоскости a и b пересекаются.
2.  плоскости a и b совпадают.
плоскости a и b совпадают.
3.  Þ aççb.
Þ aççb.
Расстояние от точки до плоскости

Угол между двумя плоскостями

Лекция 4
 Прямая в
Прямая в 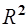 .
.
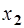 
 


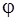
| Уравнения прямой линии в параметрической форме нам уже известны (см. пункт 1, формула (2)). Но в случае, когда прямая лежит в пространстве 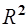 ,есть более удобныеуравнения прямой, которые будем использовать при решении задач. ,есть более удобныеуравнения прямой, которые будем использовать при решении задач.
|
1.Общим уравнением прямой  называется уравнение вида
называется уравнение вида 

Как и в случае плоскости можно показать, что если  то
то  , а если
, а если 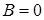 , то
, то  и вектор
и вектор  .
.
2.Уравнение прямой с угловым коэффициентом:
 .
. 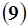
Геометрический смысл числа  состоит в том, что
состоит в том, что  , где
, где  - угол, образованный
- угол, образованный  с положительным направлением
с положительным направлением  .
.
Пусть заданы две прямые
 и
и 
Тогда:

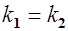
то есть у параллельных прямых угловые коэффициенты равны.


то есть у перпендикулярных прямых угловые коэффициенты обратны по величине и противоположны по знаку(Действительно, так как  и
и 
 , то
, то 

3. Уравнение пучка прямых проходящих, через точку  , записывается в виде:
, записывается в виде:


4. Уравнение прямой, проходящей через две точки  и
и  , имеет вид:
, имеет вид:
 или
или  .
. 
Взаимное расположение прямых
Пусть относительно общей декартовой системы координат заданы две прямые:  и
и  .
.
 Þ
Þ  или
или  или
или  – условие пересечения двух прямых на плоскости.
– условие пересечения двух прямых на плоскости.
 – условие совпадения двух прямых на плоскости.
– условие совпадения двух прямых на плоскости.
 Þ
Þ  или
или  – условие параллельности двух прямых на плоскости.
– условие параллельности двух прямых на плоскости.
