 .
.
Угол между двумя прямыми
 .
.
Лекция 5
Кривые (линии) второго порядка
Линии на плоскости, которые в прямоугольной декартовой системе координат задаются алгебраическими уравнениями второй степени называются линиями второго порядка. Наиболее распространёнными среди линий 2-го порядка являются эллипсы (окружность – частный случай эллипса), гиперболы, параболы.
Эллипсом называют множество точек плоскости, сумма расстояний каждой из которых до двух данных фиксированных точек  и
и  равна длине данного отрезка
равна длине данного отрезка  , причём
, причём  . Точки
. Точки  и
и  называются фокусами эллипса, а расстояние между фокусами – фокальным расстоянием.
называются фокусами эллипса, а расстояние между фокусами – фокальным расстоянием.
Если М – точка данного эллипса, то отрезки 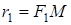 и
и 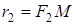 называются фокальнымирадиусами точки М.
называются фокальнымирадиусами точки М.
Обозначают  . По определению
. По определению 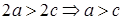 ,
,  , т.е.
, т.е.  .
.
Уравнение  является каноническим уравнением эллипса.
является каноническим уравнением эллипса.
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине его большой оси  .
.
Так как  , то
, то 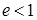 , т.е. эксцентриситет каждого эллипса меньше 1:
, т.е. эксцентриситет каждого эллипса меньше 1:  .
.
Для окружности имеем  , следовательно
, следовательно  .
.
Выражения для фокальных радиусов эллипса:  .
.
Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии, равном 
 от него, называются директрисами эллипса.
от него, называются директрисами эллипса.
Уравнения директрис в выбранной системе координат имеют вид  (левая директриса) и
(левая директриса) и  (правая директриса).
(правая директриса).
Так как 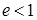 , то
, то  . Следовательно, правая директриса расположена правее правой вершины эллипса. Аналогично, левая директриса расположена левее его левой вершины.
. Следовательно, правая директриса расположена правее правой вершины эллипса. Аналогично, левая директриса расположена левее его левой вершины.
Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний каждой из которых до двух данных фиксированных точек F 1 и F 2 равен длине данного отрезка PQ, причём PQ < F 1 F 2.
Точки F 1 и F 2 называются фокусами гиперболы, а расстояние между ними – фокальным расстоянием, F 1 F 2= 2с. Если М – точка гиперболы, то отрезки F 1 М = r 1 и F 2 М = r 2 называются фокальными радиусами точки М.
F 1 F 2=2 с, PQ =2 a, 2 a <2 c Þ a < c.
По определению гиперболы 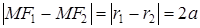 .
.
 - каноническое уравнение гиперболы
- каноническое уравнение гиперболы
Прямые, определяемые уравнениями  , называется асимптотой гиперболы.
, называется асимптотой гиперболы.
Отношение расстояния от центра гиперболы до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и обозначается буквой е:  .
.
Так как для гиперболы 0 < а < с, то е >1, т.е. эксцентриситет гиперболы больше 1.
Выражения для фокальных радиусов гиперболы
 где
где 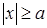 .
.
Две прямые, перпендикулярные действительной оси гиперболы и отстоящие от центра гиперболы на расстоянии  , называются директрисами гиперболы:
, называются директрисами гиперболы:  .
.
Две гиперболы, заданные уравнениями  и
и  в одной и той же прямоугольной декартовой системе координат с одними и теми же значениями полуосей a и b, называются сопряжёнными.
в одной и той же прямоугольной декартовой системе координат с одними и теми же значениями полуосей a и b, называются сопряжёнными.
Парабола
Рассмотрим прямую d и точку F Ï d. Параболой называется множество точек плоскости, расстояния каждой из которых до d и до некоторой фиксированной точки F плоскости одинаковы. Точка F называется фокусом параболы, прямая d – директрисой параболы.
Расстояние от фокуса параболы до её директрисы называется параметром параболы,  . Эксцентриситет параболы принимается равным единице:
. Эксцентриситет параболы принимается равным единице:  .
.
I.  . Рассмотрим параболу со смещённой вершиной:
. Рассмотрим параболу со смещённой вершиной:  . Вершина этой параболы находится в точке
. Вершина этой параболы находится в точке  .
.
II. 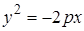 . Эта парабола симметрична параболе
. Эта парабола симметрична параболе  относительно оси
относительно оси  . Все точки этой параболы расположены левее этой оси:
. Все точки этой параболы расположены левее этой оси:  . Теперь переместим вершину этой параболы в точку
. Теперь переместим вершину этой параболы в точку  , получим
, получим  .
.
III.  . Эта парабола имеет своей осью симметрии ось
. Эта парабола имеет своей осью симметрии ось  , параметр обозначили через
, параметр обозначили через  . Ветви её направлены вверх. Переместим вершину этой параболы в точку
. Ветви её направлены вверх. Переместим вершину этой параболы в точку  , получим
, получим  .
.
IV.  . Парабола симметрична относительно оси
. Парабола симметрична относительно оси  , ветви направлены вниз. Переместим вершину этой параболы в точку
, ветви направлены вниз. Переместим вершину этой параболы в точку  , получим
, получим  .
.
Теорема (без доказательства). Пусть в декартовой системе координат задано уравнение второго порядка  . Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:
. Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:

| эллипс | |

| мнимый эллипс | |

| две мнимые пересекающиеся прямые (точка) | |

| гипербола | |

| две пересекающиеся прямые | |

| парабола | |

| две параллельные прямые | |

| две мнимые параллельные прямые | |

| две совпадающие прямые |
Уравнению мнимого эллипса и уравнению пары мнимых параллельных прямых не удовлетворяет ни одна точка действительной плоскости.