4.1. Записать в таблицу 1.1 температуру окружающей среды t ср (измеряется термометром) и среднюю температуру поверхности трубы t ст.
4.2. Рассчитать площадь поверхности трубы по формуле:
.
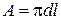4.3. Определить конвективную составляющую теплового потока Q к как разность: Q к = Q полн – Q изл,
где Q изл – поток излучения с поверхности трубы. В соответствии с законом Стефана-Больцмана он определяется по формуле:
,
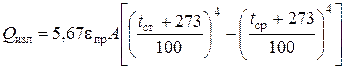где eпр – приведенная степень черноты излучающей поверхности трубы в условиях эксперимента.
4.4. Вычислить коэффициент теплоотдачи, используя формулу (1.1).
4.5. Вычислить критерии Нуссельта по формуле 1.2. Это значение будет являться экспериментальным значением Nuэксп.
4.6. Определить значение числа Грасгофа (1.3).
4.7. Определить значение произведения (Gr×Pr) и, используя выражения (1.6) – для горизонтально расположенной трубы или выражения (1.7) или (1.8) в зависимости от значения (Gr×Pr) – для вертикально расположенной трубы найти теоретическое значение числа Nuтеор. Численное значение критерия Прандтля и теплофизические свойства воздуха выбрать по температуре окружающей среды из приложения 1. Полученные значения занести в таблицу 1.1.
4.8. Определить относительную погрешность измерений
(%).
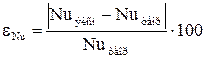5. Контрольные вопросы и дополнительные задания
1. Что называется конвективным теплообменом? Какие различают виды конвекции?
2. Динамический и тепловой пограничные слои и их физический смысл?
3. Что называют коэффициентом теплоотдачи, от каких величин он зависит?
4. Какими числами подобия характеризуется конвективный теплообмен?
5. Опишите механизм возникновения свободного потока воздуха.
6. Изобразите траектории свободного движения воздуха около горячей горизонтальной, вертикальной трубы.
7. Одинаковые ли будут коэффициенты теплоотдачи при одинаковом температурном напоре и противоположных направлениях теплового потока (от поверхности трубы и от воздуха к поверхности).
8. Как изменится численное значение критерия Грасгофа, если диаметр трубы увеличить в два раза? Как это повлияет на коэффициент теплопроводности при прочих одинаковых условиях?
9. Как изменится коэффициент теплоотдачи, если труба будет расположена вертикально, а температурный напор останется прежним?
10. Определить толщину теплового пограничного слоя на цилиндрической поверхности нагретой трубы.
Лабораторная работа № 2
ИССЛЕДОВАНИЕ ТЕПЛОВОГО ИЗЛУЧЕНИЯ ТВЕРДОГО ТЕЛА
Цели работы:
1. Определить степень черноты поверхности твердого тела.
2. Рассчитать длину волны излучения, соответствующую максимуму спектральной излучательности.
Оборудование и материалы: лабораторная установка для изучения теплового излучения
Теоретические сведения
В основу методики определения степени черноты тела положена формула лучистого теплового потока между двумя телами, одно из которых находится в объеме, ограниченном поверхностью другого:
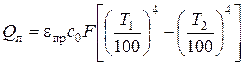, (2.1)
Где с 0 = 5,67 Вт/(м2К4)–коэффициент излучения абсолютно черного тела;
F – площадь поверхности излучения испытуемого тела, м2;
Т 1 – температура поверхности испытуемого тела, К;
Т 2 – температура окружающих тел, которую можно принять равной температуре воздуха в лаборатории, К;
eпр – приведенная степень черноты, которая в условиях эксперимента равна степени черноты испытуемого тела, так как площадь его поверхности много меньше площади поверхности окружающих тел.
В условиях сложного радиационно-конвективного теплообмена лучистый тепловой поток Q л, определяется как разность между полным Q и конвективным Q к тепловыми потоками от испытуемого тела в окружающую среду:
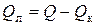, (2.2)
где Q = W в условиях стационарного режима.
Величину конвективного теплового потока можно определить по формуле Ньютона:
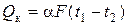, (2.3)
где t 1, t 2 – температуры поверхности тела и окружающей среды,
a – коэффициент теплоотдачи, Вт/(м2К).
Средний коэффициент теплоотдачи рассчитывается с помощью уравнений подобия. Применение теории подобия позволяет обобщить результаты экспериментальных исследований теплоотдачи в виде критериальных уравнений для
конкретного класса явлений. Критериальные уравнения подобия теплоотдачи устанавливают зависимость критерия Нуссельта от определяющих критериев (Pr, Gr). Как правило, эти уравнения представляются в виде степенных функций. В условиях свободной конвекции критериальное уравнение имеет вид:
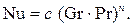(2.4)
Эмпирические коэффициенты c и n, входящие в уравнение (5), определяются путем статистической обработки многочисленных экспериментальных данных.
Для теплоотдачи с поверхности горизонтальной трубы при свободной конвекции в диапазоне величин 5×102 < Gr×Pr < 2×107 эти коэффициенты имеют постоянные значения:
c = 0,5; n = 0,25,
а критериальное уравнение теплоотдачи принимает следующий вид:
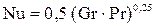. (2.5)
Опыт показывает, что при температурном перепаде ³ 1°С для горизонтальных труб и цилиндров уже выполняется условие 5×102 < Gr×Pr, поэтому режим обтекания воздухом нагретой трубы всегда турбулентный и при расчетах нужно использовать уравнение (2.5).
Для вертикальных труб за характерный геометрический размер принимается высота трубы, а вид критериального уравнения определяется интенсивностью свободного движения:
– ламинарный режим (10 3 < Gr× Pr < 10 9), c = 0,76; n = 0,25;
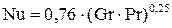; (2.6)
– турбулентный режим (Gr× Pr > 10 9) c = 0,15; n = 0,33;
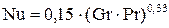(2.7)
Для данной лабораторной установки смена режимов обтекания трубы воздухом, при её вертикальном расположении происходит при мощности нагревателя ~10¸12 Вт, что соответствует температурному перепаду ~15¸20 °С.
Практическое использование эмпирических уравнений подобия заключается в нахождении коэффициентов теплоотдачи по значению Nu, вычисленному из критериального уравнения для данного класса явлений.
Теория конвективного теплообмена позволяет определить коэффициенты теплоотдачи для подобных случаев теплообмена путем обобщения экспериментальных данных. Для этого применяются критериальные числа подобия:
· критерий Нуссельта, характеризующий интенсивность конвективного теплообмена
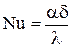, (2.8)
где l – коэффициент теплопроводности окружающей среды, Вт/(м×К);
d – характерный геометрический размер теплоотдающей поверхности, который для горизонтально расположенной трубы принимается равным наружному диаметру (d = d), а для вертикально расположенной ее длине (d = l), м;
· критерий Грасгофа, характеризующий интенсивность и режим свободного движения
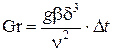, (2.9)
где g – ускорение свободного падения, м/с2;
b – коэффициент объемного расширения, который для газов может быть определен из закона Гей–Люссака в виде
b = 1 /(t cр+273),K -1;
n – кинематическая вязкость окружающей среды, м2/с;
· критерий Прандтля, характеризующий соотношение механических (вязкостных) и тепловых свойства теплоносителя
Pr = n / а, (2.10)
где а – коэффициент температуропроводности окружающей среды, м2/с.
После того, как из выбранного уравнения подобия найден коэффициент теплоотдачи, по формуле (2.3) определяется конвективный тепловой поток, из выражения (2.2) - лучистый поток, и, в конечном итоге, из уравнения (2.1) степень черноты тела.
Лабораторная установка
Теплоотдающей поверхностью в опытах по определению коэффициента теплоотдачи конвективного теплообмена служит поверхность металлической трубы (рис. 2.1).
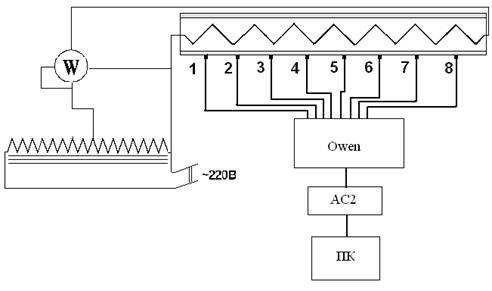
Рис. 2.1. Схема установки
Внутри трубы, установленной на стойках, находится электрический нагреватель, мощность которого регулируется автотрансформатором и измеряется ваттметром. Мощность нагревателя W в условиях стационарного теплового режима равна полному тепловому потоку Q полн с поверхности нагретой трубы в окружающую среду.
Теплотехнические измерения на данной лабораторной установке включают в себя измерения тепловых потоков и температур. Для определения температуры стенки трубы на ее наружной поверхности закреплены измерительные спаи восьми хромель-копелевых термопар. Выходы термопар подключены к прибору ОВЕН УКТ38-Щ4, который осуществляет измерение температуры и через адаптер АС2 передает данные на компьютер.