Ряды Маклорена и Тейлора

Лекция 18.

Степенные ряды. Ряды Тейлора и Маклорена.

Вопросы:

1. Степенные ряды. Теорема Абеля.

2. Понятие радиуса и интервала сходимости степенногоряда.

3. Ряды Тейлора и Маклорена.

4. Разложение в ряд Маклорена элементарных функций.

5. Применение рядов к приближенным вычислениям.

6. Ряды Фурье.

Степенные ряды. Теорема Абеля

Определение 8.13. Степенным рядом называется функциональный ряд

а ₀ +а ₁ х+а ₂ х ² +…+а_nхⁿ+…, (8.17)

или

а ₀ +а ₁(х-х ₀) +а ₂(х-х ₀)² +…+а_n (х-х ₀) ⁿ+…

Членами ряда (8.17) являются степенные функции u_n = а_nхⁿ, где а_n — некоторые постоянные величины, которые называются коэффициентами данного ряда.

Если х =0, то сумма ряда (8.17) равна а ₀, следовательно область сходимости любого степенного ряда является непустым множеством.

Теорема 8 ( Абеля). Если степенной ряд (8.17) сходится при х=х₀≠ 0, то он сходится абсолютно при любых значениях х, для которых имеет место неравенство

ç х ç < ç х ₀ç.

Из этой теоремы следует, что степенные ряды сходятся на интервале (-R,R), где число R> 0 таково, что при ç х ç <R ряд (8.17) сходится, при ç х ç >R — расходится.

Определение 8.14. Число R называют радиусом сходимости степенного ряда (8.17).

Определение 8.15. Интервал (-R;R), внутри которого степенной ряд сходится, а вне его расходится, называется интервалом сходимости степенного ряда.

Замечание. Для степенных рядов интервал сходимости
(х ₀ –R,х ₀ +R).

Применяя признак Даламбера (или радикальный признак) к ряду ç а ₀ç + ç а ₁ х ç +…+ ç а_nхⁿ ç +..., получим формулы для вычисления радиуса сходимостистепенного ряда:

,

(или из радикального признака Коши):

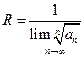.4

Пример 8.11. Найти область сходимости степенного ряда

(8.18)

Решение. Так как , то .

Интервал сходимости х є(- 1, 1), ряд расходится при .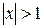

Таким образом, чтобы найти область сходимости и расходимости, надо провести исследование при х =±1, т.е. на концах интервала сходимости.

Подставив х= 1, получим числовой ряд , который по признаку Лейбница сходится. При х= -1 получим — расходящийся гармонический ряд.

Итак, область сходимости ряда — промежуток (-1,1], область расходимости —
(-∞,-1] È (1,+∞).

Свойства степенных рядов

Теорема 8. Сумма степенного ряда s (x) определена и непрерывна для всех х, принадлежащих интервалу сходимости.

Теорема 9. Если степенной ряд а ₀ +а ₁ х+…+а_nхⁿ+…=s (x) сходится в интервале (-R,R), то ряд, полученный почленным дифференцированием членов этого ряда имеет тот же интервал сходимости и

а ₁ + 2 а ₂ х+…+nа_nхⁿ־¹+…=S¢ (x).

Теорема 10. Степенной ряд можно почленно интегрировать в области сходимости.

Пример 8.12. Найти сумму S (x) ряда

Решение. Продифференцируем почленно этот ряд, при этом получим ряд:

.

Следовательно, и +C. Так как S (0)=0, то С =0 и S (x)=ln|1- х|.

Таким образом, ln | 1 -х|= 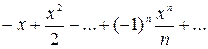при х є(- 1,1).

Подставив, например, , можно найти сумму числового ряда

Ряды Маклорена и Тейлора

В последнем примере показано, что некоторая функция может быть записана в виде степенного ряда. Возможно, ли решить обратную задачу — по заданной функции найти степенной ряд (разложить функцию f (x)в степенной ряд).

Определение 8.16. Если функция f (x)бесконечно дифференцируемав окрестности точки х ₀, то можно записать степенной ряд вида

, (8.19)

который называется рядом Тейлора для функции f (x).

Если х ₀=0, то ряд (8.19) называется рядом Маклорена и имеет вид:

Определение 8.17. Формула называется формулой Маклорена.

Соответственно, формулой Тейлора является формула:

.

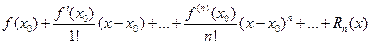Как указано ранее (п. 8.3.1), остаточный член R_n (х) также является рядом, но его можно задать в другом виде:

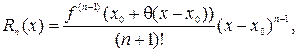
Замечание. Для любой элементарной функции существует х ₀и R, такие, что в интервале (х_о-R,х_о+R) она может быть разложена в ряд Тейлора или, если х ₀=0, в ряд Маклорена.