Приведем ряды Маклорена основных элементарных функций.
I. Показательная функция f (x)= ex.
Рассмотрим f (х) =еx, она определена и бесконечно дифференцируема на всей числовой оси и f(n) (х) =еx. При х 0 = 0 будет f ( n )(0) = 1. Тогда ряд Маклорена для этой функции имеет вид:
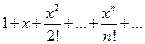
Найдем радиус сходимости этого ряда

Тогда интервал сходимости (- ∞,∞). Можно доказать, что 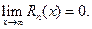 Значит,
Значит,
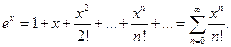
II. Тригонометрические функции 
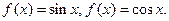
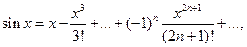 R=∞,
R=∞,
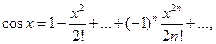 R=∞.
R=∞.
Ряд для cos x легко можно получить, продифференцировав предшествующий ряд функции sin x.
III. 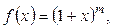 где m — любое действительное число.
где m — любое действительное число.
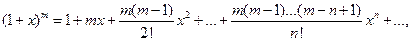 R =1.
R =1.
Этот ряд называется биноминальным.
IV. Логарифмическая функция 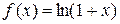 .
.
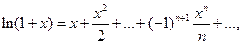 R =1.
R =1.
V. f (х) = arctg x.
Непосредственное применение формулы Маклорена к f (х) = arctg x приводит к громоздким вычислениям производных, поэтому используем теорему 2.
(arctg x)'= 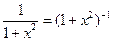 .
.
Разложение в ряд Маклорена функции (1 +х 2)-1 можно найти, используя биноминальный ряд:
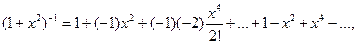 R =1.
R =1.
Интегрируя, находим ряд
 R= 1.
R= 1.
При х= ±1, получаем знакочередующиеся числовые ряды:
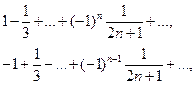
сходимость которых следует из теоремы Лейбница. Итак,
 при хє [-1,1].
при хє [-1,1].
Применение рядов к приближенным вычислениям
В приближенных вычислениях степенные ряды играют исключительно большую роль. Например, с помощью их составлены таблицы тригонометрических функций, таблицы логарифмов, которые применяются в различных областях знаний.
Пример 8.13. Разложить в ряд Маклорена функцию f (х) =  .
.
Решение.
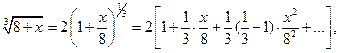 интервал сходимости
интервал сходимости 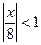 , т.е. ç х ç<8.
, т.е. ç х ç<8.
Пример 8.14. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение. Подставив вместо х в ряд функции ех выражение –х 2, найдем ряд для е-х ²:
 R=
R= 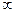 .
.
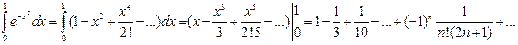
Для полученного знакочередующегося ряда выполнения условия теоремы Лейбница, его остаток | Rn (x)|< an +1. Таким образом, нужно найти an +1<Δ, где Δ=0,001:
a 0=1, a 1 =  , a 2 =
, a 2 = 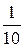 , a 3 =
, a 3 = 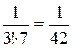 , a 4 =-
, a 4 =-  , a 4 =
, a 4 =  .
.
Значит,
 1–0,3333+0,1000–0,0238+0,0046=0,7475»0,747.
1–0,3333+0,1000–0,0238+0,0046=0,7475»0,747.
Ряды Фурье
Рассмотрим тригонометрический ряд
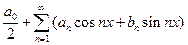 (8.20)
(8.20)
Пусть задана периодическая функция f(х)=f(х+2p), тогда полагаем
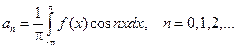 (8.21)
(8.21)
 (8.22)
(8.22)
Формулы (8.21; 8.22) называются формулами Фурье.
Определение 8.18. Тригонометрический ряд, коэффициенты аn и bn которого найдены по формулам Фурье называется рядом Фурье для функции f (х).
Символически это записывается так
 ~
~  .
.
В общем случае поставить знак = в место ~ нельзя, поскольку ряд (8.20) может расходиться или сходиться, но его сумма не совпадет с f (х).
Теорема 1. Если f (х)кусочно-непрерывная и ограниченная на (-p,p) функция, имеющая кусочно-непрерывную производную f' (х), то ее ряд Фурье сходится. Его сумма S (x) =f (x) в точках непрерывности функции f (x). В точках разрыва 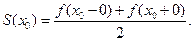
Теорема 2. Ряд Фурье (8.20) интегрируемой на интервале (-p,p) функции f (x) можно интегрировать в этом интервале.
Широкое применение ряда Фурье имеют при анализе сезонных или других периодических изменений во временных рядах.
Пример 8.15. Пусть f (x) =х, где хє (- p,p).

Тогда ряд Фурье
 . (8.23)
. (8.23)

 График f (x): y
График f (x): y
 p
p



-p 0 p x
 -p
-p
 График S (x): y
График S (x): y

 p
p
 | |||||
 | |||||
 | |||||



 x
x
 -3p -p 0 p 3p
-3p -p 0 p 3p
 -p
-p
Как и степенные ряды, ряды Фурье можно использовать для вычисления сумм числовых рядов.
Например, подставим в ряд (8.23) 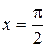 .
.
Тогда  ,отсюда
,отсюда  .
.
С помощью переменной можно преобразовывать выражение коэффициентов Фурье для функций с любым периодом Т= 2 l на интервале [ a–l,a+l ].
ЛИТЕРАТУРА
Для содержательных модулей
1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.