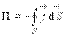В квантовой механике моменту импульса ставится в соответствие оператор: 
Оператор квадрата момента импульса дается формулой: 
Чтобы найти собственные значения операторов момента, перейдём к сферической системе координат:
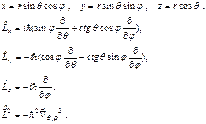
 - оператор Лапласа для сферы (угловая часть оператора Лапласа),
- оператор Лапласа для сферы (угловая часть оператора Лапласа), 
Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта, характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.
Некоторые квантовые числа связаны с движением в пространстве и характеризуют вид волновой функции частицы. Это, например, радиальное (главное) ( ),орбитальное (
),орбитальное ( ), магнитное (
), магнитное ( ) и спиновое квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента, его проекция на заданную ось и спин частицы, соответственно.
) и спиновое квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента, его проекция на заданную ось и спин частицы, соответственно.
Оператор гамильтона
Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, компоненты которого являются частными производными по координатам.  ,
,
Этот оператор приобретает смысл в сочетании со скалярной или векторной функцией, к которой он применяется.
Если скалярно умножить вектор  на функцию
на функцию  , то получится вектор
, то получится вектор 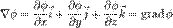
Если вектор  скалярно умножить на вектор
скалярно умножить на вектор  , получится скаляр
, получится скаляр  то есть дивергенция вектора
то есть дивергенция вектора 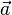 .
.
Стационарное уравнение Шрёдингера
Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда  не является функцией времени, можно записать в виде:
не является функцией времени, можно записать в виде: 
где функция 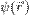 должна удовлетворять уравнению:
должна удовлетворять уравнению: 
Уравнение непрерывности
Дифференциальная форма общего уравнения непрерывности  где ∇ — дивергенция, t — время, j — плотность потока, σ — добавление q на единицу объёма в единицу времени. Члены, которые добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками» соответственно. Если q — сохраняющаяся величина, которая не может быть создана или уничтожена (например, энергия), тогда σ = 0, и уравнение непрерывности принимает вид:
где ∇ — дивергенция, t — время, j — плотность потока, σ — добавление q на единицу объёма в единицу времени. Члены, которые добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками» соответственно. Если q — сохраняющаяся величина, которая не может быть создана или уничтожена (например, энергия), тогда σ = 0, и уравнение непрерывности принимает вид: 
Уравнение Шредингера учитывает свойства симметрии пространства и времени. Поэтому из основного уравнения квантовой механики могут быть получены такие общие законы, как закон сохранения массы, закон сохранения заряда и другие законы сохранения.
Чтобы показать это, выделим в пространстве некоторый объем  , ограниченный замкнутой поверхностью
, ограниченный замкнутой поверхностью  . В квантовом состоянии с заданной волновой функцией
. В квантовом состоянии с заданной волновой функцией  вероятность нахождения частицы в рассматриваемом объеме определяется как
вероятность нахождения частицы в рассматриваемом объеме определяется как 
.
Если эта вероятность изменяется со временем, то следует предположить наличие потока вероятности П через поверхность  , который и приводит к изменению вероятности
, который и приводит к изменению вероятности  :
:  Считая поток вероятности П распределенным по всей поверхности
Считая поток вероятности П распределенным по всей поверхности  , введем вектор плотности потока вероятности
, введем вектор плотности потока вероятности 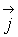 , определив его интегральным соотношением
, определив его интегральным соотношением