В задачах 1 – 10 найти решение системы уравнений при помощи определителей по формулам Крамера и методом Гаусса.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
В заданиях 11-20 найти указанные пределы:
11. а) 
; б) 
.
12. а) 
; б) 
.
13. а) 
; б) 
.
14. а) 
; б) 
.
15. а) 
; б) 
.
16. а) 
; б) 
.
17. а) 
; б) 
.
18. а) 
; б) 
.
19. а) 
; б) 
.
20. а) 
; б) 
.
В заданиях 21 – 30 требуется исследовать данные функции и построить их графики. Исследование функции предусматривает нахождение области определения, точек экстремума, интервалов возрастания и убывания, а также точек перегиба и интервалов выпуклости и вогнутости графиков функции.
21. у = х 3 – 9 х 2 + 15 х - 3. 2 2. у =(х 2 + 1)(х + 2).
23. у = 1 + 3 х 2 – х 3. 2 4. у = х 3 + 6 х 2 + 9 х.
25. у = х 3 – 12 х + 1. 2 6. у = 8 х 2 – 5 х - х 3.
27. у = х 2 (х - 1) 2 8. у = х 2 (4 – х).
29. у = х 3 + 3 х 2 - 3. 3 0. у = - х (х – 1)2.
В задачах 31-40 найти частные производные функции двух независимых переменных х и у:
31. а) z = x 2– 3 x y + 5 y 2 – 7 x 2 y 2 + 13; б) 
.
32. а) z = x 5– 5 x 4 y 3 + 2y 5 – x 2 y 2 + 3; б) 
.
33. а) z = x 4– 3x y 3 - 2 x 2 y 2+ 5 y 4 –23; б) 
.
34. а) z = x 3– 2 x y 2 + x 3 y 2+ 7 y 3 – 0,4; б) 
.
35. а) z = x 2– 4 x 2 y 2 +8 x 3 y + 11 y 4 – 0,14; б) 
.
36. а) z = x 3– 9 x y 2 +3 x 4 y 2+ 
y 3 – 0,64; б) 
.
37. а) z = x 4– 3x 3 y 3 - 2 x y 2+ 
y 4 –2,5; б) 
.
38. а) z = x 4–5 x 3 y + 4 x y 3+ 
y 5 –32,1; б) 
.
39. а) z = x 3– 9 x y 2 +3 x 4 y + 0,2 y 10 – 0,21; б) 
.
40. а) z = x 2– 3 x 3 y + x 4 y 3+ 12 y 2 – 1,13 б) 
.
В заданиях 41-50 вычислить площадь фигуры, ограниченной линиями:
41. у = 6 х – х 2, у = 0. 42. у = х 3, у = 8, х = 0.
43. у = 4 – х 2, у = 0. 44. у = х 2, у = 2 – х 2.
45. у = х 2,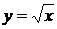 
. 46. ху = 4, х = 4, у = 4, х = 0, у = 0.
47. у = х 2, у = 1. 48. у = х 3, у = 2 – х, у = 0.
49. у = х 2 - 4 х, у = 0. 50. 
, у = х.
51. Монету бросают 5 раз. Найти вероятность того, что «орел» выпадет: а) менее двух раз; б) три раза; в) более трех раз.
52. В семье 5 детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков. Вероятность рождения мальчика равна 0,51.
53. В корзине находятся яблоки, 10% которых являются червивыми. Найти вероятность того, среди 7 наугад взятых яблок: а) не будет червивых; б) одно будет червивым; в) будет менее шести доброкачественных.
54. Всхожесть семян пшеницы 90%. Найти вероятность того, что из шести наугад взятых зерен: а) взойдут не менее четырех; б) более четырех; в) взойдут все.
55. Вероятность того, что посаженое дерево приживется 0,75. Найти вероятность того, что из 5 посаженых деревьев приживется: а) менее трех; б) четыре; в) не более четырех.
56. Вероятность попадания в цель при одном выстреле равна 0,7. Производится 4 выстрела. Найти вероятность того, что цель будет поражена: а) три раза; б) не более двух раз; в) не менее 3 трех
раз.
57. Вероятность сбоя станка - автомата в течение смены равна 0,2. В цехе работают четыре таких станка. Найти вероятность того, что в течение смены произойдут сбои а) одного станка; б) всех станков; в) не более двух станков.
58. По статистическим данным 60% семей некоторого населенного пункта имеют телефоны. Случайным образом выбирают 6 семей. Какова вероятность того, что среди них телефоны имеют: а) все семьи; не более трех семей; в) хотя бы одна семья.
59. Из двадцати посаженых яблонь в среднем приживаются 17. На дачном участке было посажено 6 яблонь. Найти вероятность того, что приживется: а) три яблони; б) не менее четырех; в) более пяти.
60. Вероятность поломки картофелеуборочного комбайна в течение рабочего дня составляет 0,3. Какова вероятность того, что в течение 4 рабочих дней: а) поломка комбайна произойдет только один раз; б) не более двух раз; в) поломок комбайна вообще не будет.
В заданиях 61-70 задан закон распределения дискретной случайной величины X. Вычислить ее математическое ожидание, дисперсию и среднее квадратичное отклонение.
61.
| X | -4 | ||||
| Р | 0,15 | 0,1 | 0,2 | 0,2 | 0,35 |
62.
| X | -2 | -1 | |||
| Ρ | 0,15 | 0,2 | 0,2 | 0,35 | 0,1 |
63.
| Х | |||||
| Ρ | 0,1 | 0,25 | 0,3 | 0,2 | 0,05 |
64.
| Χ | -1 | ||||
| Ρ | 0,15 | 0,2 | 0,25 | 0,3 | 0,1 |
64.
| Χ | |||||
| Ρ | 0,5 | 0,2 | 0,15 | 0,1 | 0,05 |
65.
| Χ | -3 | -2 | -1 | ||
| Ρ | 0,35 | 0,2 | 0,15 | 0,1 | 0,2 |
66.
| Χ | -4 | -3 | -2 | -1 | |
| Ρ | 0,15 | 0,35 | 0,25 | 0,15 | 0,1 |
67.
| Χ | -1 | ||||
| Ρ | 0,15 | 0,25 | 0,35 | 0,15 | 0,1 |
68.
| Х | -3 | -2 | -1 | ||
| Ρ | 0,2 | 0,35 | 0,2 | 0,15 | 0,1 |
69.
| Χ | |||||
| Ρ | 0,1 | 0,3 | 0,25 | 0,2 | 0,15 |
70.
| Х | |||||
| Ρ | 0,15 | 0,2 | 0,2 | 0,3 | 0,15 |
В заданиях 71-80. Исходными данными являются результаты обследования выборки, где наблюдалась непрерывная случайная величина. Составить интервальный ряд распределения, разбив диапазон значений случайной величины на 5 интервалов, и начертить гистограмму распределения плотности относительных частот. Данные взять из таблицы 1.
Таблица 1.
| Номер наблю- дения | Данные для задач | |||||||||
| 44,1 | 11,9 | 7,0 | 0,8 | 16,6 | ||||||
| 22,6 | 9,5 | 3,7 | 4,8 | 13,9 | ||||||
| 24,8 | 16,6 | 1,2 | 2,0 | 11,8 | ||||||
| 29,4 | 14,8 | 1,0 | 1,8 | 13,1 | ||||||
| 40,8 | 9,5 | 7,1 | 2,2 | 14,5 | ||||||
| 21,1 | 10,8 | 1,0 | 3,3 | 7,7 | ||||||
| 26,6 | 11,7 | 2,7 | 3,2 | 10,1 | ||||||
| 32,4 | 10,4 | 0,4 | 2,7 | 6,6 | ||||||
| 33,1 | 11,5 | 9,8 | 1,9 | 14,3 | ||||||
| 25,7 | 12,2 | 8,0 | 2,9 | 14,5 | ||||||
| 37,1 | 10,5 | 4,3 | 3,1 | 10,2 | ||||||
| 31,4 | 8,4 | 4,5 | 3,7 | 11,7 | ||||||
| 32,4 | 10,1 | 5,8 | 2,8 | 11,4 | ||||||
| 38,2 | 15,2 | 7,1 | 2,4 | 10,5 | ||||||
| 44,5 | 17,3 | 1,6 | 2,2 | 11,0 | ||||||
| 42,8 | 11,1 | 6,3 | 4,6 | 12,4 | ||||||
| 39,3 | 13,4 | 2,6 | 3,1 | 13,7 | ||||||
| 28,8 | 11,0 | 3,4 | 0,3 | 11,6 | ||||||
| 20,5 | 10,4 | 0,7 | 1,7 | 10,2 | ||||||
| 30,3 | 14,2 | 9,4 | 2,6 | 9,7 |