ФГБОУ ВПО
«Ярославская государственная сельскохозяйственная академия»
Кафедра математики и информационных технологий
К.А.Зиновьев, Е.С. Рогозина
А.З. Скопец, Л.П. Щипина
Математика.
Методические указания и контрольные
Задания для студентов-заочников 1 курса
Экономического факультета
по направлению
080200.62 «Менеджмент»
Ярославль 2012
Порядок выполнения контрольных работ.
К выполнению каждой контрольной работы следует приступать только после изучения соответствующего материала в учебной литературе, список которой дан в каждой главе, и примеров решений задач, приведенных в данном пособии. Можно также использовать ресурсы сети Internet (адреса: www.boockland.ru и www.mathelp.spb.ru).
При этом необходимо руководствоваться следующими указаниями:
1. Контрольную работу следует выполнять в отдельной тетради, на обложке которой должны быть указаны фамилия и инициалы студента, полный шифр, номер контрольной работы и дата её отправки в академию. Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо делать полностью, чертежи должны быть выполнены аккуратно и четко, с указанием координатных осей, единиц масштаба и других элементов.
2. Студент выполняет тот вариант контрольной работы, который совпадает с последней цифрой номера его зачетной книжки. Например, если номер зачетной книжки студента 02076, то он решает все задачи шестого варианта. Номера задач указаны в табл. 1.
3. Незачтённая работа возвращается студенту, который должен в кратчайший срок выполнить все требования рецензента и представить ее на повторное рецензирование вместе с первоначальным текстом.
Таблица 1
| Последняя цифра номера зачетной книжки | Н о м е р а з а д а ч | ||||||||
Тема1. Элементы линейной алгебры
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 10.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 14, 15.
Методические указания.
Решение систем трех линейных уравнений с тремя неизвестными методом Крамера.
Система трех линейных уравнений с тремя неизвестными имеет вид
. (2)
Решением системы (2) называется такая тройка чисел (х;у;z), которая при подстановке в систему обращает каждое уравнение в верное равенство.
Главным определителем системы (2) называется определитель третьего порядка, составленный из коэффициентов при неизвестных:
.
Вспомогательные определители системы (2) получаются из главного определителя заменой соответствующего столбца столбцом свободных членов.
; 
; 
.
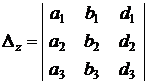Если главный определитель системы не равен нулю, т.е. ∆ ≠ 0, то система (2) имеет единственное решение, которое находится по формулам Крамера:
; 
, 
.
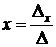Если главный определитель системы равен нулю, т.е. ∆ = 0, а хотя бы один из вспомогательных не равен нулю, т.е. ∆х ≠ 0 или ∆у ≠ 0 или ∆z ≠ 0, то система (2) не имеет решений и называется несовместной.
Если главный определитель системы равен нулю, т.е. ∆ = 0, и все вспомогательные равны нулю, т.е. ∆х = 0 и ∆у = 0 и ∆z = 0, то система (2) имеет бесконечное множество решений и называется неопределенной.
Примеры решения задач.
Задача 1. Решить систему
.
Решение. 
= 
=
= 2(1∙(-1) - (-1)∙(-2)) + 3(1∙(-1) - 3∙(-2)) + 5(1∙(-1) - 3∙1) =
= 2(-1-2) + 3(-1+6) + 5(-1-3) = -6 + 15 - 20 = -11;
= 
=
= (1∙(-1) - (-1)∙(-2)) + 3((-4)∙(-1) – (-2)∙(-2)) + 5((-4)∙(-1) – (-2)∙1) =
= (-1-2) + 3(4-4) + 5(4+2) = -3 + 0 + 30 = 27.
Аналогично вычисляются вспомогательные определители 
и 
:
=45; 
= 14.
Так как ∆ ≠ 0, то система имеет единственное решение.
; 
, 
.
Ответ: 
.
Решение систем линейных уравнений методом Гаусса.
Система m линейных уравнений с n неизвестными имеет вид:
(1)
Коэффициенты при неизвестных составляют прямоугольную матрицу А, содержащую m строк и n столбцов. Если матрица дополнена столбцом свободных членов, то она называется расширенной матрицей системы –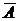 
.
Величины aij называются элементами матрицы, i = 1,2,… m, j = 1,2,… n.
Если m = n, то матрица А называется квадратной. Диагональ матрицы, составленная из элементов a11, a22, … ann называется ее главной диагональю.
Решением системы линейных уравнений (1) называется совокупность n чисел k 1, k 2, …, k n такая, что при подстановке ее вместо неизвестных каждое из уравнений системы (1) обращается в равенство.
Если система не имеет решений, то она называется несовместной. Если система имеет одно решение, то она называется определенной. Если система линейных уравнений имеет более одного решения, то она называется неопределенной.
Две системы линейных уравнений называются равносильными (эквивалентными), если множества их решений совпадают.
Рассмотрим метод последовательного исключения неизвестных или метод Гаусса решения системы линейных уравнений. С помощью преобразований, которые не нарушают равносильность системы уравнений, а именно:
а) перестановка уравнений в системе;
б) умножение обеих частей любого уравнения на число, отличное от нуля;
в) прибавление к одному уравнению системы другого, умноженного на любое число отличное от нуля, от системы (1) переходят к системам вида:
(2)
или 
(3)
Система (2) называется системой треугольного вида, а система (3) – системой трапецеидального вида.
В системе (2) из последнего уравнения находится х n, затем, подставив его значение в предпоследнее уравнение, находим x n-1. Продолжая далее, найдем, что система (2), а следовательно и система (1) обладает единственным решением.
Если система приведена к виду (3), то переменным x k+1, x k+2, … x n можно придавать произвольные значения и затем решать как систему (2). В этом случае переменные x k+1, x k+2, …, x n называются свободными или независимыми переменными, а переменные x 1, x 2, …, x n называются связанными или зависимыми переменными.
При решении системы линейных уравнений методом Гаусса для приведения ее к виду (2) или (3) следует выписать расширенную матрицу системы и выполнить над строками матрицы следующие элементарные преобразования:
а) перестановка местами двух строк;
б) умножение элементов некоторой строки на число, отличное от нуля;
в) прибавление к элементам i- ой строки соответствующих элементов j- ой строки, умноженной на любое число.
Примеры решения задач.
Задача №2. Решить систему уравнений
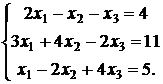
Решение. Выпишем расширенную матрицу системы
.
Преобразуем эту матрицу таким образом, чтобы элементы, стоящие ниже главной диагонали были равны нулю. Для удобства вычисления третью строку переставим на первое место
.
Умножим первую строку на –2 и прибавим ко второй строке, а затем, умножив первую строку на –3, прибавим ее к третьей строке. Получим:
→ 
.
Оставив первую и вторую строки без изменения, к третьей прибавим вторую, умноженную на –5.
.
Полученной треугольной матрице соответствует треугольная система уравнений
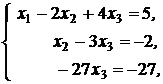
которая равносильна данной системе.
Из последнего уравнения находим х 3 = 1. Подставляя значение х 3 во второе уравнение, находим х 2
, х 2 = 1.
Подставляем найденные значения х 3 и х 2 в первое уравнение системы и находим х 1
, х 1 = 3.
Система имеет единственное решение.
Ответ: х 1 = 3; х 2 = 1; х 3 = 1.
Вопросы для самопроверки.
1. Как решается система уравнений методом Крамера?
2. Запишите систему m линейных уравнений с n неизвестными в общем виде. Что называется решением этой системы?
3. В чем состоит метод Гаусса?
4. Какие равносильные преобразования можно выполнять над уравнениями системы?
5. Какая система называется совместной; несовместной; неопределенной?
6. Как найти общее решение неопределенной системы? Как можно получить частное решение системы?
7. Дайте определение матрицы.
Тема 2. Введение в математический анализ.
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 1, 2, 4.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 2, 3.
Методические указания.
Математический анализ – это раздел математики, посвященный изучению свойств и закономерностей функциональных зависимостей.
Функциональной зависимостью называется такая взаимосвязь одной или нескольких независимых переменных величин с некоторой, зависимой от них, переменной величиной, при которой каждому значению независимых переменных соответствует строго определенное значение этой зависимой переменной.
Математическое выражение, устанавливающее вид взаимосвязи зависимой переменной с независимой, называется функцией и обозначается строчной латинской буквой f. Независимая переменная называется аргументом функции, и, как правило, обозначается строчной латинской буквой х, а зависимая переменная – у.
Например, 
. Здесь функцией является выражение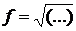 
. Если 
, то функция имеет вид 
.
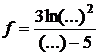Для функциональных зависимостей существует понятие области допустимых значений аргумента, то есть совокупности таких значений аргумента, при которых функция будет определена. Очевидно, если 
, то х не может быть отрицательным, при 
, х не может быть равным единице и т.п.
Примеры решения задач.
Задача №3. Найти предел функции 
.
Решение. При непосредственной подстановке предельного значения х = 3, получаем неопределенность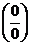 
. Для раскрытия неопределенности сократим дробь 
, предварительно разложив на множители числитель и знаменатель дроби
= 
= 
= 
.
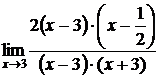Задача №4. Найти предел функции
.
Решение. При непосредственной подстановке предельного значения х = 0, получаем неопределенность 
. Для раскрытия неопределенности умножим числитель и знаменатель дроби 
на выражение 
, сопряженное знаменателю, и произведем необходимые преобразования
= 
=
=
= 
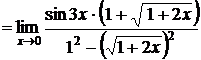
= –3.
При нахождении данного предела использовался первый замечательный предел. Так как 
, то 
.
Вопросы для самопроверки.
1. Сформулируйте определение функции одной независимой переменной.
2. Что называется областью определения функции? Областью значений функции?
3. Какая функция называется возрастающей? Убывающей?
4. Дайте определение максимума и минимума функции, точки максимума и точки минимума функции.
6. Какая функция называется четной? Нечетной?
7. Какая функция называется периодической?
8. Какая функция называется сложной?
9. Дайте определения, сформулируйте основные свойства, начертите графики основных элементарных функций.
10. Что называется числовой последовательностью?
11. Что называется пределом числовой последовательности?
12. Сформулируйте основные теоремы о пределах.
13. Какая переменная величина называется бесконечно большой? Бесконечно малой? Какая связь между ними?
14. Сформулируйте основные свойства бесконечно малых величин.
15. Что представляет собой первый замечательный предел?
16. Что представляет собой второй замечательный предел?
17. Дайте определение непрерывности функции в точке, в интервале.
18. Какая точка называется точкой разрыва функции?
Тема 3. Производная и дифференциал функции.