Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 5,6.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 4,5.
Методические указания.
Производной функции называется выражение, характеризующее быстроту изменения функции при изменении ее аргумента. Например, если мы имеем функцию 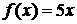 , то, очевидно, быстрота ее изменения равна 5, то есть изменение аргумента на единицу приводит к изменению значения функции на 5 единиц. (
, то, очевидно, быстрота ее изменения равна 5, то есть изменение аргумента на единицу приводит к изменению значения функции на 5 единиц. ( , а
, а  ).
).
В общем случае производная функции определяется как предел отношения приращения функции  к приращениюее аргумента
к приращениюее аргумента  . Очевидно, что если
. Очевидно, что если  , то
, то  , и
, и 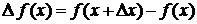 .
.
Производная функции обозначается штрихом около символа функции  . Таким образом, согласно определению
. Таким образом, согласно определению
 .
.
Примеры решения задач.
Задача №5. Исследовать функцию  с помощью производной и построить ее график.
с помощью производной и построить ее график.
Решение. Исследование функции предусматривает нахождение области определения, точек экстремума и интервалов возрастания и убывания, а также точек перегиба и интервалов выпуклости и вогнутости графиков функции.
1. Находим область определения функции.
Выражение  имеет смысл при любом действительном значении аргумента х, следовательно, областью определения функции является множество действительных чисел
имеет смысл при любом действительном значении аргумента х, следовательно, областью определения функции является множество действительных чисел  .
.
2. Находим первую производную заданной функции:
 или
или  .
.
3. Критическими точками функции 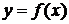 называются точки, в которых производная
называются точки, в которых производная  равна нулю или не существует. Найдем их:
равна нулю или не существует. Найдем их:
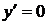 , т. е.
, т. е.  или
или  , откуда
, откуда 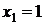 и
и  . Других критических точек нет.
. Других критических точек нет.
4) Обращение производной функции в нуль или ее отсутствие в точках, где функция определена, есть лишь необходимое условие существования экстремума функции в этих точках.
Достаточным условием существования экстремума функции в критической точке, входящей в область определения функции, является изменение знака производной первого порядка при переходе через эту точку. В частности, если производная меняет знак с плюса на минус, то в критической точке функция имеет максимум. Если же при переходе через критическую точку производная меняет знак с минуса на плюс, то в этой точке функция имеет минимум.
Определим, являются ли точки 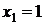 и
и  точками экстремума. Они разбивают всю числовую ось на три промежутка, (рис. 1), знак производной в которых определим с помощью «пробной» точки.
точками экстремума. Они разбивают всю числовую ось на три промежутка, (рис. 1), знак производной в которых определим с помощью «пробной» точки.
 ● ●
● ●
1 5 х
Рис. 1
В интервале (–∞; 1) возьмем, например, точку х = 0. Тогда
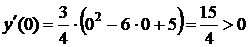 .
.
В интервале (1; 5) возьмем точку х = 2. Очевидно
 .
.
Наконец, в интервале (5; ∞) возьмем точку х = 6. Тогда
 .
.
Следовательно, точка х = 1 есть точка максимума данной функции, а точка х = 5 – точка минимума. Найдем значение функции в точках экстремума:
у max = y (1) = 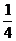 (13 – 9∙12 + 15∙1 – 3) = 1.
(13 – 9∙12 + 15∙1 – 3) = 1.
у min = у (5) = 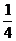 (53 – 9∙52 + 15∙5 – 3) = – 7.
(53 – 9∙52 + 15∙5 – 3) = – 7.
5. Если производная  функции положительна внутри некоторого промежутка, то функция
функции положительна внутри некоторого промежутка, то функция  возрастает на этом промежутке. Если же производная
возрастает на этом промежутке. Если же производная  отрицательна внутри некоторого промежутка, то функция
отрицательна внутри некоторого промежутка, то функция  убывает на этом промежутке.
убывает на этом промежутке.
Очевидно, данная функция возрастает на промежутках (–∞; 1) и (5; ∞), а убывает на промежутке (1; 5).Результат исследований п. 4 и п. 5 удобно представить в виде схемы.

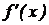 + – +
+ – +



 • •
• •
 1 5 х
1 5 х
точка точка
max min
Рис. 2
6. Найдем вторую производную у ″(х) данной функции
у ″(х) = 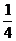 (3 х 2 – 18 х + 15)′ =
(3 х 2 – 18 х + 15)′ = 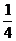 (6 х – 18).
(6 х – 18).
Найдем точки, в которых вторая производная функции равна нулю
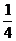 (6 х - 18) = 0, откуда х = 3.
(6 х - 18) = 0, откуда х = 3.
Точка х = 3 разбивает всю числовую ось на два интервала (–∞; 3) и (3; ∞). В интервале (–∞; 3) возьмем, например, точку х = 0 и определим в ней знак второй производной
у ″(0) = 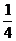 (6∙0 – 18) =
(6∙0 – 18) =  < 0.
< 0.
В интервале (3; ∞) возьмем, например, точку х = 4, тогда
у ″(4) = 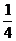 (6∙4 – 18) =
(6∙4 – 18) =  > 0.
> 0.
Если вторая производная f ″(х) положительна внутри некоторого промежутка, то график этой функции  на этом промежутке вогнутый вверх (или выпуклый вниз). Если же вторая производная f ″(х) внутри некоторого промежутка отрицательна, то график функции
на этом промежутке вогнутый вверх (или выпуклый вниз). Если же вторая производная f ″(х) внутри некоторого промежутка отрицательна, то график функции  на этом промежутке выпуклый вверх (или вогнутый вниз).
на этом промежутке выпуклый вверх (или вогнутый вниз).
Очевидно, на интервале (–∞; 3) график данной функции выпуклый вверх, а на промежутке (3; ∞) – вогнутый вверх.
7. Если вторая производная f ″(х) в некоторой точке х 0, принадлежащей области определения функции, обращается в нуль и при переходе через эту точку меняет знак, то точка 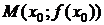 является точкой перегиба графика функции
является точкой перегиба графика функции  . Итак, х = 3 – абсцисса точки перегиба. Найдем ее ординату
. Итак, х = 3 – абсцисса точки перегиба. Найдем ее ординату
у (3) = 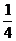 (33 – 9∙32 + 15∙3 – 3) =
(33 – 9∙32 + 15∙3 – 3) = 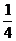 (–12) = –3.
(–12) = –3.
Таким образом, точка (3; -3) - точка перегиба графика функции.
8. Строим график функции у = 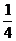 (х 3 – 9 х 2 + 15 х – 3) (рис.3).
(х 3 – 9 х 2 + 15 х – 3) (рис.3).

Рис. 3
Вопросы для самопроверки.
1. Дайте определение производной функции.
2. Каков геометрический смысл производной?
3. В чем заключается физический смысл производной?
4. Сформулируйте правила дифференцирования суммы, произведения, частного.
5. Приведите формулы дифференцирования основных элементарных функций.
6. Сформулируйте правило дифференцирования сложной функции.
7. Что называется дифференциалом функции? Каков его геометрический смысл?
8. Что называется производной второго порядка? Каков физический смысл производной второго порядка?
1. Сформулируйте признаки возрастания (убывания) функции в данном промежутке.
2. Какие точки называются критическими? Как найти эти точки?
3. Сформулируйте необходимые условия существования экстремума функции.
4. Сформулируйте достаточные признаки существования экстремума функции.
5. Дайте определение выпуклости, вогнутости кривой.
6. Что называется точкой перегиба графика функции?
7. Какова схема исследования функции на экстремум с помощью производной?
Тема 4. Функции нескольких переменных.
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 11, 12.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 10.
Примеры решения задач.
Задача №6. Найти частные производные функции
z = 6 x 4 – 3 x 3 y + 3 xy 2 – 6 y 5 + 0,2 по х и у.
Решение. При нахождении частной производной по х, переменная у считается постоянной
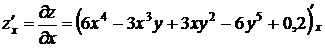 =
=
 =
=
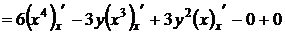 =
= 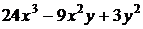 .
.
При нахождении частной производной по у, переменная х считается постоянной
 =
=
 =
=
 =
= 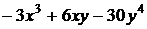 .
.
Задача №7. Найти частные производные функции
 .
.
Решение. При нахождении частной производной по х переменная у считается постоянной
 =
=
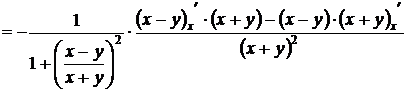 =
=
 =
=
 =
=


 .
.
При нахождении частной производной по у, переменная х считается постоянной.
 =
=
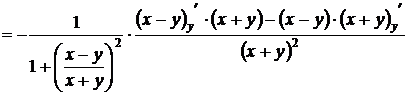 =
=
 =
=

= 

 .
.
Вопросы для самопроверки.
1. Сформулируйте определение функции двух независимых переменных.
2. Дайте определение частных производных функции двух независимых переменных.
3. Запишите формулу для вычисления полного дифференциала функции двух независимых переменных.
4. Как находятся частные производные второго порядка функции двух независимых переменных?
Тема 5. Определенный интеграл и его приложения.
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 8.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 7.
Методические указания
Под определенным интегралом  от данной непрерывной функции
от данной непрерывной функции  на данном отрезке [ a; b ] понимается соответствующее приращение ее первообразной, то есть
на данном отрезке [ a; b ] понимается соответствующее приращение ее первообразной, то есть
 .
.
Числа а и b называются соответственно верхним и нижним пределом интегрирования. Обычно разность 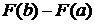 обозначают как
обозначают как  , в силу чего формулу определенного интеграла обычно записывают так
, в силу чего формулу определенного интеграла обычно записывают так
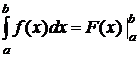 ,
,
причем следует помнить, что сначала подставляется верхний предел интегрирования, а затем нижний.
Определенный интеграл имеет также геометрический смысл, заключающийся в том, что он равен площади криволинейной трапеции, то есть такой трапеции, одна из непараллельных сторон которой представляет собой график функции  на интервале [ a; b ].
на интервале [ a; b ].
Вычисление определенных интегралов также представляет собой приведение с помощью различных приемов данного интеграла к табличному
Примеры решения задач.
Задача № 8. Вычислить определенный интеграл
 .
.
Решение. Данный интеграл приводится к табличному с помощью подстановки t = ln x. Отсюда  . Определим пределы интегрирования новой переменной. При х = 1, t = ln1 = 0, при х = е, t = lne = 1. Произведем замену переменной и используем формулу Ньютона–Лейбница.
. Определим пределы интегрирования новой переменной. При х = 1, t = ln1 = 0, при х = е, t = lne = 1. Произведем замену переменной и используем формулу Ньютона–Лейбница.
 =
=  =
=  = arcsin1 – arcsin0 =
= arcsin1 – arcsin0 =  .
.
Задача № 9. Найти площадь фигуры, ограниченной линиями:
y = x 2,  , y = 0, x = 2 (x > 0).
, y = 0, x = 2 (x > 0).
Решение. Данную фигуру можно разбить на две криволинейные трапеции, площади которых соответственно равны: S1 и S2. (Рис. 4).
Тогда S = S1 + S2. Найдем абсциссу точки А –точки пересечения двух линий.

Отсюда  , или х 4 = 1, то есть х 1 = –1 и х 2 = 1. Так как по условию x > 0, то абсцисса точки А равна 1.
, или х 4 = 1, то есть х 1 = –1 и х 2 = 1. Так как по условию x > 0, то абсцисса точки А равна 1.

 у
у

 2,0
2,0 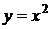
 1,5
1,5


 1,0
1,0
 |





 0,5 у = 1/ х
0,5 у = 1/ х
 |
0 0,5 1,0 1,5 2,0 2,5 х
Рис. 4.
Следовательно,
 =
=  ,
,  и тогда
и тогда
 (кв.ед.).
(кв.ед.).
Задача №10. Найти площадь фигуры, ограниченной параболой
 и прямой y = x + 2.
и прямой y = x + 2.
Решение. 1. Изобразим данные линии на чертеже и заштрихуем фигуру, площадь которой нужно найти. Графиком функции  является парабола. Найдем производную данной функции и, приравняв ее к нулю, определим критическую точку.
является парабола. Найдем производную данной функции и, приравняв ее к нулю, определим критическую точку.
 .
.
Пусть y ′ = 2 – х = 0. Отсюда х = 2. Это – абсцисса вершины параболы. Ордината вершины  . Ветви параболы направлены вниз. Найдем точки пересечения параболы с осью О х, положив у = 0. Тогда
. Ветви параболы направлены вниз. Найдем точки пересечения параболы с осью О х, положив у = 0. Тогда  или
или  . Решив данное квадратное уравнение, получим х 1 = -2 и х 2 = 6. Строим параболу (рис. 5).
. Решив данное квадратное уравнение, получим х 1 = -2 и х 2 = 6. Строим параболу (рис. 5).
 |
у



 8
8
 |
 у = х + 2
у = х + 2


 6
6
 |

 4
4
 |
 2
2
 | |||||
 | |||||
 |
–2 0 2 4 6 х
Рис. 5.
2. Графиком функции у = х + 2 является прямая, для ее построения достаточно двух точек. При х = 0, у = 2, при х = 2, у = 4. Строим прямую.
3. Площадь фигуры, ограниченной сверху непрерывной кривой 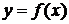 , снизу – непрерывной кривой
, снизу – непрерывной кривой  находится по формуле:
находится по формуле:
 ,
,
где a и b – абсциссы точек пересечения кривых.
Для нахождения точек пересечения данных линий, решим систему уравнений:

 , или
, или  .
.
Решая полученное квадратное уравнение, получим х 1 = –2 и х 2 = 4, следовательно, а = –2; b = 4. Применяя формулу площади, составим интеграл

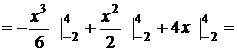
 .
.
Итак, искомая площадь S = 18 (кв. ед.).
Вопросы для самопроверки.
1. Дайте определение определенного интеграла от данной функции на заданном отрезке?
2. Каков геометрический смысл определенного интеграла?
3. Напишите формулу Ньютона-Лейбница.
4. Сформулируйте свойства определенного интеграла.
5. Как используется способ подстановки для вычисления определенного интеграла?
6. Напишите формулу интегрирования по частям для вычисления определенного интеграла.
7. Как вычисляется площадь плоской фигуры в прямоугольной системе координат с помощью определенного интеграла?
Тема 6. Повторные независимые испытания.
Литература: 1. Гмурман В.Е. Теория вероятностей и математическая статистика. «Высшая школа». М. 2003.Глава 5.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. «Высшая школа». М. 2004.Гл. 3.
Методические указания.
Методы теории вероятностей широко применяются в различных областях естествознания, техники, экономики.
Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Будем понимать под событием результат испытания. Все события можно разделить на три вида: достоверные, невозможные, случайные. Случайное – событие, которое при определенных условиях может либо произойти, либо нет. На практике случайное событие есть следствие многих случайных причин и учесть их влияние невозможно. Если рассматривать многократно повторяющиеся при одних и тех же условиях события, то имеют место определенные закономерности, которые называются вероятностными.
Основным понятием теории вероятностей является вероятность события.
Вероятностью Р события А называется отношение числа исходов m, благоприятствующих появлению события А, к числу n всех несовместны и равновозможных исходов испытания.

Вероятность события принимает значения от 0 до 1.
Если производится несколько независимых испытаний, причем вероятность события в каждом испытании не зависит от исходов других испытаний, то такие испытания называются повторными независимыми относительно события А. Если при этом вероятность появления события А в каждом испытании одна и та же, то они называются повторными независимыми испытаниями. Для того, чтобы определить вероятность того, что в n независимых повторных испытаниях событие А наступит ровно m раз используются формулы Бернулли, Лапласа, Пуассона. Для нахождения вероятности того, что событие А наступит от m 1 до m 2 раза используется интегральная теорема Лапласа.
Примеры решения задач.
Задача №11. Вероятность прорастания семян огурцов равна 0,8. Какова вероятность того, что из 5 посеянных семян прорастут: а) три; б) не менее четырех.
Решение. Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна p, то вероятность что событие А появится в этих n испытаниях т раз, выражается формулой Бернулли
 , где
, где  ,
,  .
.
а) В нашем случае, p = 0,8, n = 5, m = 3, q =1 – p. Следовательно,
 .
.
б) Прорастание не менее 4 семян означает, что должно взойти либо четыре, либо пять растений. Пусть событие А означает, что из 5 семян взойдут не менее 4 семян; событие В – из 5 взойдут 4; D – из 5 взойдут 5. Поскольку события В и D несовместны, вероятность наступления события А равна сумме вероятностей этих событий
Р (А) = Р (В) + Р (D)
Вероятность события В
 .
.
Для события D, m = n, значит  , и вероятность наступления события D
, и вероятность наступления события D
 .
.
Таким образом, вероятность того, что из пяти посеянных семян взойдут не менее четырех
 .
.
Вопросы для самопроверки.
1. Что составляет предмет теории вероятностей?
2. Какое событие называется случайным, невозможным, достоверным?
3. Сформулируйте определение вероятности события.
4. Какие действия над событиями Вы знаете?
5. Какие события называются повторными, независимыми?
6. В каких случаях применяются формулы Бернулли, Лапласа, Пуассона?
Тема 7. Случайные величины.
Литература: 1. Гмурман В.Е. Теория вероятностей и математическая статистика. «Высшая школа». М. 2003.Главы 6 -8.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. «Высшая школа». М. 2004.Гл. 5.
Примеры решения задач.
Задача 12. Задан закон распределения случайной дискретной величины X. Вычислить ее математическое ожидание, дисперсию и среднее квадратичное отклонение.
| X | -3 | -1 | |||
| р | 0,1 | 0,2 | 0,3 | 0,25 | 0,15 |
Решение. Математическое ожидание случайной дискретной величины
 .
.
В нашем случае
 .
.
Дисперсия случайной дискретной величины
 .
.
Для нахождения математического ожидания квадрата случайной величины  составим закон ее распределения
составим закон ее распределения
| Х2 | |||||
| р | 0,1 | 0,2 | 0,3 | 0,25 | 0,15 |
Тогда
 .
.
 .
.
Среднее квадратичное отклонение случайной величины X
 .
.
Вопросы для самопроверки
1. Что такое дискретная случайная величина и ее ряд распределения?
2. Дайте определение числовых характеристик случайной величины и объясните их смысл.
Тема 8. Элементы математической статистики.
Литература: 1. Гмурман В.Е. Теория вероятностей и математическая статистика. «Высшая школа». М. 2003.Главы 15 - 19.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. «Высшая школа». М. 2004.Гл. 9-13.
Методические указания.
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой - либо более или менее обширной совокупности, обладающих теми или иными признаками.
Различные значения признака, наблюдающиеся у членов совокупности, называются вариантами. Число mi, показывающее, сколько раз встречается вариант в совокупности, называется его частотой, а отношение частоты варианта к числу n членов совокупности – его относительной частотой 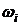 , где i принимает значения от 1 до k - числа различных вариант.
, где i принимает значения от 1 до k - числа различных вариант.
 , i = 1,2,3,…, k.
, i = 1,2,3,…, k.
Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариант с соответствующими им относительными частотами.
Вся подлежащая изучению совокупность объектов называется генеральной совокупностью.
Экономически невыгодно производить обследование всей совокупности, если по результатам изучения сравнительно небольшой ее части можно получить с достаточной для практики достоверностью необходимую информацию о всей совокупности. Такой метод исследования носит название выборочного.
Пусть имеется ряд распределения значений признака. Для того, чтобы подвергнуть его анализу рассматриваются постоянные величины, которые характеризуют ряд в целом и отражают присущие изучаемой совокупности закономерности. К таким постоянным относятся средние арифметические, дисперсии, средние квадратические отклонения.
Примеры решения задач.
Задача № 13. Известны урожайности в центнерах на один гектар яровой пшеницы в 20 хозяйствах: 13,9; 12,4; 13,1; 6,3; 11,8; 11,6; 10,5; 10,4; 10,6; 11,3; 15,1; 11,7; 11,3; 10,2; 11,0; 10,7; 8,2; 9,6; 10,2; 15,1. Получить интервальный ряд распределения и начертить гистограмму.
Решение. Записываем исходные данные в виде ранжированного ряда: 6,3; 8,2; 9,6; 10,2; 10,2; 10,4; 10,5; 10,6; 10,7; 11,0; 11,3; 11,3; 11,6; 11,7; 11,8; 12,4; 13,1; 13,9; 15,1; 15,1.
Рассматривая этот ряд, видим, что диапазон изменения вариант в выборке составляет 6 – 16.
Весь диапазон изменения вариант в выборке разбиваем на несколько интервалов. Размер интервала выбирается произвольно, но следует иметь в виду, что чем меньше интервал, тем точнее результаты. В данном случае принимаем размер интервала равным 2 единицам (∆ xi = 2). Получаем пять интервалов: первый 6 – 8, второй 8 – 10, третий 10 – 12, четвертый 12- 14, пятый 14 – 16.
Определяем частоту попадания вариант выборки в каждый интервал. В первый интервал попадает одно значение (6,3) из ряда, поэтому m 1 = 1. Во второй интервал попадает два значения (8,2 и 9,6), поэтому m 2 = 2. Аналогично получаем m 3 = 12, m 4 = 3, m 5 = 2.
Определяем относительные частоты попадания вариант выборки в каждый интервал:
в первый интервал - 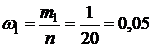 .
.
во второй интервал -  ,
,
в третий интервал -  ,
,
в четвертый интервал -  ,
,
в пятый интервал -  .
.
Проверяем правильность расчетов. Для этого суммируем относительные частоты:
 = 0,05 + 0,10 + 0,60 + 0,15 + 0,10 = 1,00.
= 0,05 + 0,10 + 0,60 + 0,15 + 0,10 = 1,00.
Сумма всех относительных частот равна единице, следовательно, вычисления произведены правильно.
Определяем плотность относительных частот вариант как отношение относительной частоты ωi к размеру интервала ∆ xi:
для первого интервала -  ;
;
для второго интервала -  ;
;
для третьего интервала -  ;
;
для четвертого интервала -  ;
;
для пятого интервала -  .
.
Результаты вычислений сводим в таблицу 2.
Таблица 2.