Выявить аномальные значения уровней ряда позволяет метод Ирвина.
Рассчитываются значения статистики Ирвина для всех уровней ряда, начиная со второго по формуле:
, 
;
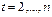где 
, и 
.
Полученные значения сравниваем с критическим значением 
-статистики.
Критические значения статистики Ирвина на уровне значимости 
| N | |||||||
| 2,8 | 2,3 | 1,5 | 1,3 | 1,2 | 1,1 | 1,0 |
Если 
, временной ряд не содержит аномальных значений, иначе соответствующий уровень ряда является аномальным и для дальнейшего исследования такого ряда требуется провести предварительное сглаживание.
Исследование временного ряда на наличие тренда
Опр. Тренд – это устойчивая тенденция во временном ряду более или менее свободная от случайных колебаний.
| Виды трендовых моделей | |||
| Название функции | Описание функции | Название функции | Описание функции |
| 1.Линейная | 
| 6.Медифицированная экспонента |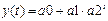 
|
| 2.Парабола второго порядка | 
| 7.Кривая Гомперца | 
|
| 3.Кубическая парабола | 
| 8.Логистическая кривая | 
|
| 4.Показательная | 
| 9.Логарифмическая парабола | 
|
| 5.Экспоненциальная | 
| 10.Гиперболическая | 
|
Для определения наличия тренда у временного ряда используют метод проверки разности средних двух частей одного и того же ряда.
.
Сперва, временной ряд разбивается на две равные части; для каждой из «половинок» рассчитывается среднее значение 
и дисперсия σ12 и σ22
По критерию Фишера проверяется гипотеза о равенстве дисперсий:
(где 
- дисперсии первой и второй части временного ряда).
Если 
, на данном уровне значимости нет оснований отвергать гипотезу о равенстве дисперсий.
Далее с помощью критерия Стьюдента проверяется гипотеза об отсутствии тренда:
,
где 
,
где n1 и n2 – объем первой и второй части временного ряда.
Если 
, на данном уровне значимости есть основания отвергнуть гипотезу об отсутствии тренда.
Пример
Имеются данные по процентному изменению заработной платы (
) за 14 лет:
| t | ||||||||||
| yt | 6,15 | 7,95 | 9,43 | 8,16 | 7,24 | 8,51 | 9,12 | 9,67 | 11,98 | 11,41 |
Задание
-провести предварительный анализ ряда;
-построить модель/
Решение
1)Проводим предварительный анализ ряда на наличие аномальных уровней, используя критерий Ирвина.
, тогда 
.
Следовательно, все расчетные значения статистики Ирвина меньше критического для данного количества наблюдений: 
,
а значит, исследуемый ряд не содержит аномальных уровней и для дальнейшего анализа не требуется дополнительного выравнивания ряда.
| t | Y | 
| 
|
| 6,15 | 7,9 | - | |
| 7,95 | 1,01 | ||
| 9,43 | 0,2 | 0,83 | |
| 8,16 | 0,6 | 0,71 | |
| 7,24 | 0,52 | ||
| 8,51 | 0,2 | 0,71 | |
| 9,12 | 0,34 | ||
| 9,67 | 0,5 | 0,31 | |
| 11,98 | 9,1 | 1,3 | |
| 11,41 | 0,32 | ||
| итого | 89,62 | 28,59 | - |
2) Проверяем гипотезу о равенстве дисперсий с помощью F- критерия Фишера.
| t | y1 | 
| t | y2 | 
|
| 6,15 | 2,68 | 8,51 | 2,65 | ||
| 7,95 | 0,03 | 9,12 | 1,04 | ||
| 9,43 | 2,70 | 9,67 | 0,22 | ||
| 8,16 | 0,14 | 11,98 | 3,39 | ||
| 7,24 | 0,30 | 11,41 | 1,62 | ||
| Cреднее | 7,786 | 1,17 | Cреднее | 10,138 | 1,78 |
(где 
).
,
значит полученное значение F-критерия меньше табличного на заданном уровне значимости, следовательно, нет оснований отвергнуть гипотезу о равенстве дисперсий.
Далее с рассчитываем:
, где 
.
,
Значит, на данном уровне значимости есть основания отвергнуть гипотезу об отсутствии тренда.