Согласно второму закону Ньютона элементарное изменение количества движения равно элементарному импульсу силы:

| (3.59) |
Здесь Р - сумма проекций на какую либо ось всех сил, приложенных к телу массой т; w - проекция скорости на ту же ось; dt - время действия силы Р.
В таком виде закон Ньютона используется в механике твердого тела. Рассмотрим элементарную струйку газа (рис. 3.7).

Рис. 3.7. Элементарная струйк а
Применим к элементарной струйке уравнение (3.59) в проекции на ось X, согласно которому сумма проекций импульсов всех сил, приложенных к массе жидкости 1 - 2, равняется изменению проекции суммарного количества движения

| (3.60) |
За время dt масса жидкости между сечениями 1 - 2 переместится и займет новое положение 1' - 2'. Изменение суммарного количества движения равно разности количеств движения жидкости в состояниях 1' - 2' и 1 - 2. Количество движения массы 1' - 2 входит как в начальное, так и в конечное значение количества движения и при вычитывании сокращается. Поэтому прирост суммарного количества движения должен быть равен разности количества движения, взятого для масс 2 - 2' и 1 - 1', которые в установившемся движении одинаковы:

Здесь dM масса жидкости элемента 1 - 1' или 2 - 2'; wX2 и wX1 - проекции на ось X скорости потока в сечениях 2 и 1.
Элементарная масса dМ равна произведению секундного массового расхода М на промежуток времени dt.
dM=Mdt.
Отсюда

Подставляя полученное выражение в (2.50), получим

или
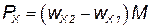
| (3.61) |
Это уравнение Эйлера, согласно которому сумма проекций всех сил, приложенных к струе жидкости, на любом ее участке равна приращению проекции секундного количества движения на этом участке.
Аналогичные уравнения можно составить и для двух других осей.
Применим уравнение количества движения (3.61) к цилиндрической струйке (рис. 3.8). Запишем сумму всех сил в проекциях на ось X, приложенных к потоку жидкости между сечениями 1 и 2. В сечении 1 на жидкость в направлении оси X действует сила Р1F, где Р1 - давление, F - площадь струйки. В сечении 2 на жидкость действует сила в противоположном направлении - Р2F.

Рис. 3.8. Схема течения в цилиндрической струйке
Суммарная сила равна F (Р1 - Р2). К потоку жидкости со стороны стенок канала приложена сила трения РТР направленная в сторону; противоположную положительному направлению оси X.
Между сечениями 1 и 2 может быть расположена какая-нибудь машина, например, турбина или компрессор, которая также оказывает силовое воздействие на поток и получает от него или отдает ему техническую работу. Принято, что если машина получает от газа работу (турбина), то сила, приложенная машиной к газу, отрицательная (- Р). Если машина (компрессор) сообщает газу техническую работу, то эта сила положительная (Р). Учитывая сказанное, сумма всех сил, приложенная к потоку, запишется в виде

| (3.62) |
С учетом (3.62) уравнение Эйлера будет иметь вид
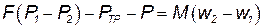
| (3.63) |
Если не учитывать силы трения (РТР=0) и наличия между сечениями 1 и 2 какой нибудь машины (Р=0), уравнение (3.63) примет вид


| (3.64) |
Если расстояние между сечениями будет бесконечно мало, то (3.64) следует записать в дифференциальной форме

Используя уравнение расхода, получим
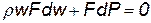
Для цилиндрической струйки (F=const)

| (3.65) |
Уравнение (3.65) выражает важное свойство газового потока. При отсутствии внешних сил и сил трения увеличение скорости потока (dw>0) может быть вызвано только уменьшением статического давления (dP<0), так как в цилиндрической струйке rw=сопst. Наоборот, торможение потока всегда связано с увеличением давления.
В интегральной форме уравнение (3.65) запишется так:

| (3.66) |
так как

то

откуда
