Полученное в предыдущем параграфе число Рейнольдса имеет большое значение в гидравлике, а также в аэродинамике, так как является одним из основных критериев гидродинамического подобия.
| Гидродинамическое подобие - это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое. |
| Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. |
В гидравлике под геометрическим подобием мы будем понимать подобие тех поверхностей, которые ограничивают потоки жидкостей, т.е. подобие русел (рис. 4.2).
| Кинематическое подобие - это подобие линий тока и пропорциональность сходственных скоростей. |

Рис. 4.2. Подобные потоки
Очевидно, что для кинематического подобия потоков требуется геометрическое подобие русел.
| Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков и равенство углов, характеризующих направление этих сил. |
В потоках жидкостей обычно действуют разные силы - давления, вязкости (трения), тяжести и др. Соблюдение пропорциональности всех этих разнородных сил означает так называемое полное гидродинамическое подобие.
Например, пропорциональность сил давления Р и сил трения Т, действующих на сходственные объемы в потоках I и II, можно записать в виде

Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных сил.
| Для напорных течений в закрытых руслах, т.е. для потоков в трубах, в гидравлических машинах и т.п., такими главными силами, как показывают расчеты, являются силы давления, трения и их равнодействующие, т.е. силы инерции. Последние, как это можно показать для подобных потоков, пропорциональны произведению динамического давления rv2/2 на характерную площадь S. |
В самом деле, для частицы жидкости, один из размеров которой равен Dl, сила равна произведению массы на ускорение, т.е.
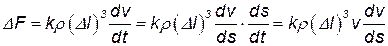
где k - безразмерный коэффициент пропорциональности, зависящий от формы частицы;
ds - элементарный путь частицы.
Умножим и разделим последнее выражение на l2 и v2cp, т.е. наряду с величинами, относящимися к частице, введем одноименные величины, характеризующие поток в целом; будем иметь
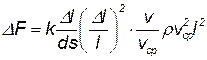
| (4.2) |
Пять безразмерных множителей в выражении для DF имеют одинаковое значение для геометрически и кинематически подобных потоков и сходственных частиц. Следовательно, заменяя знак равенства знаком пропорциональности, для этих потоков можно записать

или, так как l2 ~ S и DF ~ F, окончательно получим

| (4.3) |
Для подобных потоков I и II будем иметь

или

| Последнее отношение, одинаковое для подобных потоков, называется числом Ньютонаи обозначается Ne. |
Заметим попутно, что этому же
| произведению rv2cpS в подобных потоках пропорциональны силы, с которыми поток воздействует (или способен воздействовать) на преграды: твердые стенки, лопасти гидромашин, обтекаемые потоком тела и т.п. |
Так, например, если поток жидкости наталкивается на безграничную стенку (см. рис. 4.3), установленную нормально к нему, и в результате, растекаясь по стенке, меняет свое направление на 90°, то на основании теоремы механики о количестве движения секундный импульс силы равен

| (4.4) |
Это и есть сила воздействия на преграду. При другом угле установки стенки или другой ее форме и размерах вместо единицы будет другой коэффициент пропорциональности.

Рис. 4.3 Схема воздействия потока жидкости на преграду
Вначале рассмотрим наиболее простой случай - напорное движение идеальной жидкости, т.е. такое движение, при котором отсутствуют силы вязкости, а действие силы тяжести проявляется через давление.
Для этого случая уравнение Бернулли для сечений 1 - 1 и 2 - 2 (см. рис. 4.2) имеет следующий вид:
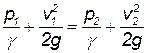
или
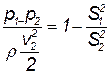
Для двух геометрически подобных потоков правая часть уравнения имеет одно и то же значение: следовательно, левая часть тоже одинакова, т.е. разности давлений пропорциональны динамическим давлениям:

| (4.5) |
| Таким образом, при напорном движении идеальной несжимаемой жидкости для обеспечения гидродинамического подобия достаточно одного геометрического подобия. |
| Безразмерная величина, представляющая собой отношение разности давлений к динамическому давлению (или разности пьезометрических высот к скоростной высоте), называется коэффициентом давления или числом Эйлера и обозначается Eu. |
Посмотрим, какому условию должны удовлетворять те же геометрически и кинематически подобные потоки, для того чтобы было обеспечено их гидродинамическое подобие при наличии сил вязкости, и, следовательно, потерь энергии, т.е. при каком условии числа Eu. будут одинаковыми для этих напорных потоков. Уравнение Бернулли теперь будет иметь следующий вид:

или
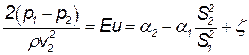
| (4.6) |
Как видно из уравнения (4.6), числа Eu будут иметь одинаковые значения для рассматриваемых потоков и потоки будут подобны друг другу гидродинамически при условии равенства коэффициентов сопротивления z (равенство коэффициентов a1 и a2 для сходственных сечений двух потоков следует из их кинематического подобия). Таким образом, коэффициенты z в подобных потоках должны быть одинаковыми, а это значит, что потери напора для сходственных участков (см. рис. 4.2) пропорциональны скоростным напорам, т.е.

Рассмотрим очень важный в гидравлике случай движения жидкости - движение с трением в цилиндрической трубе, для которого

Для геометрически подобных потоков отношение l/d одинаково, следовательно, условием гидродинамического подобия в данном случае является одинаковое значение для этих потоков коэффициента l. Последний выражается через напряжение трения на стенке t0 и динамическое давление следующим образом:

Следовательно, для двух подобных потоков I и II можно записать

| (4.7) |
т.е. напряжения трения пропорциональны динамическим давлениям.
Если использовать закон трения Ньютона и учесть, что в уравнении (4.7) v=vcр, то предыдущие отношения, обозначенные буквой k, можно выразить так:
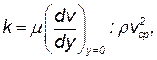
где индекс у=0 означает, что производная взята при у=0, т.е. у стенки трубы.
После умножения и деления на диаметр трубы d и перегруппировки множителей получим:

| (4.8) |
Здесь через с обозначено выражение в квадратных скобках, представляющее собой безразмерный градиент скорости у стенки. Для кинематически подобных потоков величина с одинакова, поэтому после сокращения на с условие динамического подобия потоков, (4.7) перепишется в виде

или, переходя к обратным величинам,

| В этом заключается закон подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамического подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков. |
Теперь делается понятным, почему переход от одного режима течения к другому происходит при определенном числе Re, а также выясняется физический смысл этого числа для потока в трубе, т.е. число Re есть величина, пропорциональная отношению динамического давления к напряжению трения или, что то же самое, отношению сил инерции к силам вязкости. Чем больше скорость и поперечные размеры потока и чем меньше вязкость жидкости, тем больше число Re. Для потока идеальной жидкости число Re бесконечно велико, так как вязкость n=0.
В случаях безнапорных течений под действием разности нивелирных высот вопрос о подобии осложняется, так как приходится вводить еще один критерий подобия - число Фруда, учитывающее влияние на движение жидкости силы тяжести. Однако для подавляющего большинства интересующих нас задач в области авиационной техники этот критерий не имеет значения, и мы его рассматривать не будем.
| Итак, в подобных потоках, мы имеем равенство безразмерных коэффициентов и чисел a, z, l, Eu, Ne, Re и некоторых других, которые будут введены и рассмотрены ниже. Изменение числа Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также меняться. Поэтому все эти коэффициенты в общем случае следует рассматривать как функции числа Re (хотя в некоторых интервалах числа Re они могут оставаться постоянными). |