Уравнения плоскости в пространстве. Основные задачи о плоскости. Уравнения прямой линии в пространстве. Основные задачи о прямой линии. Прямая и плоскость в пространстве. Поверхности второго порядка. [3, §12].
Пример 8. Даны точки 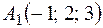 ;
;  ;
;  ;
; 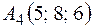 . Найти: 1) длину отрезка
. Найти: 1) длину отрезка  ; 2) уравнения прямых
; 2) уравнения прямых 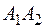 и
и 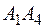 ; 3) угол между прямыми
; 3) угол между прямыми  и
и 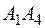 ; 4) уравнение плоскости
; 4) уравнение плоскости 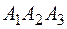 ; 5) угол между прямой
; 5) угол между прямой 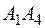 и плоскостью
и плоскостью 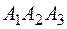 ; 6) уравнения высоты, опущенной из точки
; 6) уравнения высоты, опущенной из точки 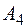 на плоскость
на плоскость 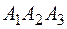 .
.
Решение:
1. Расстояние между точками  и
и 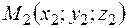 находится по формуле
находится по формуле 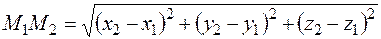 .
.
В данном случае  .
.
2. Уравнения прямой, проходящей через две заданные точки пространства  и
и 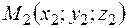 имеют вид
имеют вид 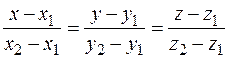 .
.
Тогда уравнения прямой  :
:  или
или 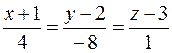 , уравнения прямой
, уравнения прямой 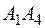 :
:  или
или 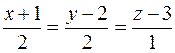 .
.
3. Острый угол между прямыми линиями, заданными уравнениями  и
и  определяется по формуле:
определяется по формуле:  .
.
Из уравнения прямой  :
: 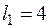 ,
,  ,
, 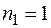 ; из уравнения прямой
; из уравнения прямой  :
:  ,
, 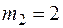 ,
, 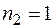 . Следовательно,
. Следовательно,

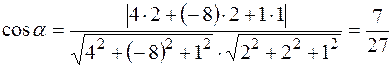 ,
,  .
.
4. Уравнение плоскости, проходящей через три заданные точки  ,
, 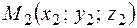 ,
, 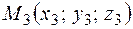 имеет вид
имеет вид  .
.
Тогда уравнение плоскости 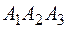 :
: 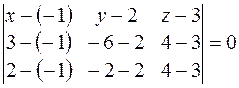 ;
;
 ;
;  .
.
5. Острый угол между прямой линией 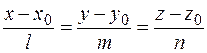 и плоскостью
и плоскостью 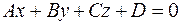 определяется по формуле:
определяется по формуле: 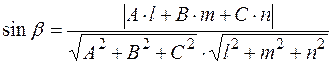 .
.
Из уравнения прямой  :
: 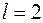 ,
,  ,
, 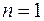 ; из уравнения плоскости
; из уравнения плоскости 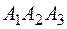 :
:  ,
,  ,
, 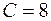 .
.
Следовательно, 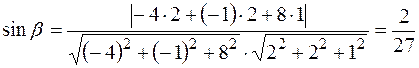 ,
,  .
.
6. Уравнения высоты, опущенной из точки 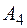 на плоскость
на плоскость 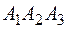 имеют вид:
имеют вид:  , где
, где  ,
, 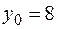 ,
, 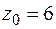 (координаты точки
(координаты точки 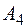 ),
),  – направляющий вектор искомой прямой.
– направляющий вектор искомой прямой.
Так как эта прямая перпендикулярна плоскости 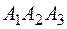 , то за вектор
, то за вектор 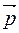 можно принять вектор нормали
можно принять вектор нормали  плоскости
плоскости 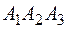 . Так как
. Так как 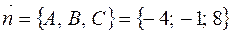 (
( ,
,  ,
,  – коэффициенты из общего уравнения плоскости
– коэффициенты из общего уравнения плоскости 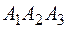 ), то
), то 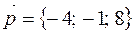 .
.
Значит, искомые уравнения имеют вид 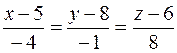 .
.
Тема 5. Введение в математический анализ
Числовые функции. График функции. Основные характеристики функции. Сложная функция. Основные элементарные функции и их графики. [3, §14]. Предел функции в точке. Односторонние пределы. Предел функции при  . [3, §16]. Основные теоремы о пределах. Первый и второй замечательные пределы. [3, §17]. Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация. Свойства функций, непрерывных на отрезке. [3, §19].
. [3, §16]. Основные теоремы о пределах. Первый и второй замечательные пределы. [3, §17]. Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация. Свойства функций, непрерывных на отрезке. [3, §19].
Пример 9. Найти пределы функций, не пользуясь правилом Лопиталя:
1) 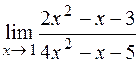 ; 2)
; 2) 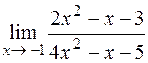 ; 3)
; 3) 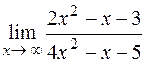 ;
;
4)  ; 5)
; 5) 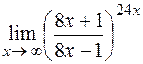 .
.
Решение:
1) 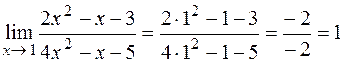 .
.
2)  .
.
Раскроем неопределенность 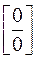 . Так как
. Так как 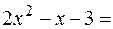
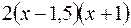 и
и 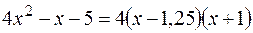 , то
, то 
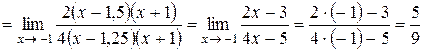 .
.
3)  .
.
Для раскрытия неопределенности 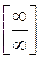 разделим числитель и знаменатель на старшую степень
разделим числитель и знаменатель на старшую степень  :
:
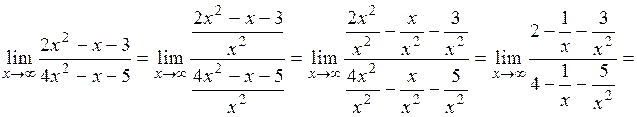
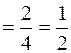 , так как
, так как 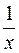 ,
,  ,
, 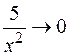 при
при 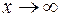 .
.
4) 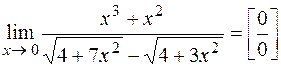 .
.
Для раскрытия неопределенности 
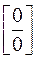 умножим числитель и знаменатель на выражение, сопряженное знаменателю:
умножим числитель и знаменатель на выражение, сопряженное знаменателю:
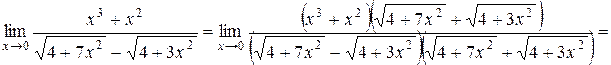
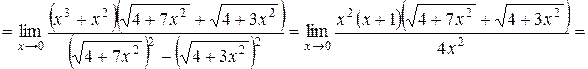
 .
.
5)  .
.
Сделаем замену  , тогда
, тогда 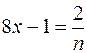 ,
,  . Так как
. Так как 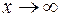 , то
, то  .
.
Тогда 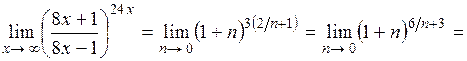

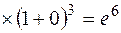 , так как
, так как 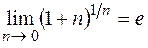 – второй замечательный предел.
– второй замечательный предел.
Пример 10. Дана функция  Найти точки разрыва функции, если они существуют, и построить ее график.
Найти точки разрыва функции, если они существуют, и построить ее график.
Решение: Функции  ,
, 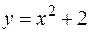 ,
, 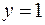 непрерывны на всей числовой прямой, поэтому заданная функция
непрерывны на всей числовой прямой, поэтому заданная функция 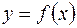 может иметь разрывы только в точках, где меняется ее аналитическое выражение, то есть в точках
может иметь разрывы только в точках, где меняется ее аналитическое выражение, то есть в точках 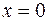 и
и  .
.
Исследуем функцию на непрерывность в этих точках. Для этого найдем соответствующие односторонние пределы и значения функции.
Рассмотрим поведение функции при 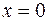 :
:
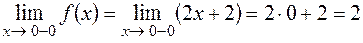 ;
;
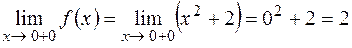 ;
; 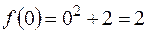 .
.
Так как 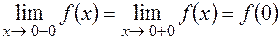 , то заданная функция непрерывна в точке
, то заданная функция непрерывна в точке 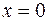 .
.
Рассмотрим поведение функции при 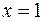 :
:
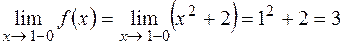 ;
; 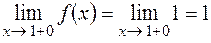 .
.
Так как пределы 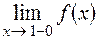 и
и  конечны и не равны, то точка
конечны и не равны, то точка 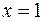 – точка разрыва I рода (функция в этой точке претерпевает «скачок» на
– точка разрыва I рода (функция в этой точке претерпевает «скачок» на 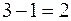 единицы).
единицы).
Сделаем чертеж:

Задачи для контрольных работ
ВАРИАНТ 1
Контрольная работа №1
1. Дана матрица 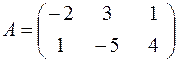 . Найти
. Найти 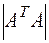 .
.
2. Решить систему линейных уравнений 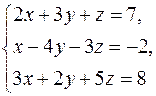
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
3. Дано: 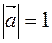 ,
, 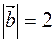 ,
, 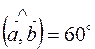 , векторы
, векторы 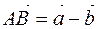 и
и 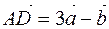 составляют стороны параллелограмма
составляют стороны параллелограмма  .
.
Найти:
1) длины диагоналей параллелограмма 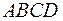 ;
;
2) острый угол между диагоналями параллелограмма 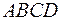 ;
;
3) площадь параллелограмма 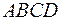 .
.
4. Даны точки  ;
; 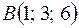 ;
; 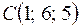 ;
; 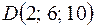 . Требуется:
. Требуется:
1) записать векторы  ,
,  ,
,  в ортонормированном базисе;
в ортонормированном базисе;
2) найти длины векторов  ,
,  ,
,  ;
;
3) показать, что векторы  ,
,  ,
,  образуют базис трехмерного пространства;
образуют базис трехмерного пространства;
4) найти острый угол между векторами  и
и  ;
;
5) найти алгебраическую проекцию вектора  на вектор
на вектор  ;
;
6) найти площадь треугольника 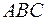 ;
;
7) найти объем пирамиды 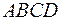 .
.
5. Найти собственные значения и собственные векторы матрицы 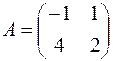 .
.
Контрольная работа №2
1. Даны координаты вершин треугольника 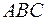 :
:  ,
,  ,
,  . Найти:
. Найти:
1) длину стороны 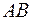 ;
;
2) уравнения сторон  и
и 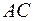 и их угловые коэффициенты; 3)
и их угловые коэффициенты; 3)  внутренний угол
внутренний угол 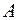 в радианах с точностью до
в радианах с точностью до 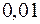 ;
;
4) уравнение высоты  и ее длину, не используя координаты точки
и ее длину, не используя координаты точки  ;
;
5) уравнение медианы 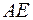 ;
;
6) точку пересечения высот треугольника 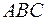 .
.
Сделать чертеж.
2. Составить уравнение прямой, проходящей через левый фокус эллипса  параллельно прямой
параллельно прямой 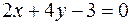 .
.
3. Даны точки 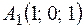 ;
; 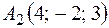 ;
;  ;
;  . Найти:
. Найти:
1) длину отрезка 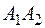 ;
;
2) уравнения прямых 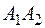 и
и  ;
;
3) угол между прямыми 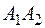 и
и  ;
;
4) уравнение плоскости 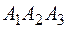 ;
;
5) угол между прямой  и плоскостью
и плоскостью 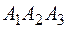 ;
;
6) уравнения высоты, опущенной из точки  на плоскость
на плоскость 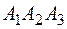 .
.
4. Найти пределы функций, не пользуясь правилом Лопиталя:
1) 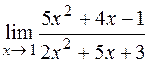 ; 2)
; 2) 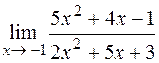 ; 3)
; 3) 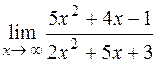 ;
;
4) 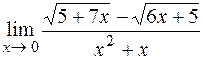 ; 5)
; 5)  .
.
5. Дана функция 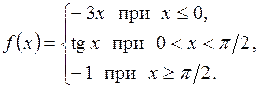
Найти точки разрыва функции, если они существуют, и построить ее график.
ВАРИАНТ 2
Контрольная работа №1
1. Дана матрица  . Найти
. Найти 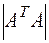 .
.
2. Решить систему линейных уравнений 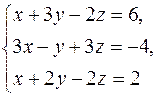
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
3. Дано: 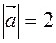 ,
, 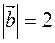 ,
, 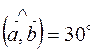 , векторы
, векторы 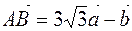 и
и  составляют стороны параллелограмма
составляют стороны параллелограмма 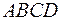 .
.
Найти:
1) длины диагоналей параллелограмма 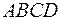 ;
;
2) острый угол между диагоналями параллелограмма 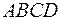 ;
;
3) площадь параллелограмма  .
.
4. Даны точки 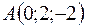 ;
; 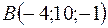 ;
; 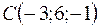 ;
; 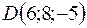 . Требуется:
. Требуется:
1) записать векторы  ,
, 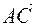 ,
, 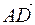 в ортонормированном базисе;
в ортонормированном базисе;
2) найти длины векторов  ,
, 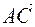 ,
,  ;
;
3) показать, что векторы  ,
, 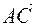 ,
, 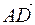 образуют базис трехмерного пространства;
образуют базис трехмерного пространства;
4) найти острый угол между векторами 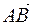 и
и  ;
;
5) найти алгебраическую проекцию вектора 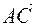 на вектор
на вектор 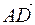 ;
;
6) найти площадь треугольника 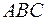 ;
;
7) найти объем пирамиды 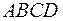 .
.
5. Найти собственные значения и собственные векторы матрицы 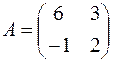 .
.
Контрольная работа №2
1. Даны координаты вершин треугольника 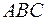 :
:  ,
,  ,
, 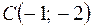 . Найти:
. Найти:
1) длину стороны  ;
;
2) уравнения сторон 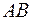 и
и 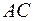 и их угловые коэффициенты;
и их угловые коэффициенты;
3) внутренний угол 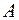 в радианах с точностью до
в радианах с точностью до 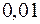 ;
;
4) уравнение высоты 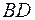 и ее длину, не используя координаты точки
и ее длину, не используя координаты точки  ;
;
5) уравнение медианы 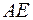 ;
;
6) точку пересечения высот треугольника 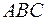 .
.
Сделать чертеж.
2. Составить уравнение прямой, проходящей через вершину параболы  параллельно прямой
параллельно прямой 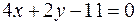 .
.
3. Даны точки 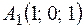 ;
; 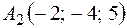 ;
;  ;
;  . Найти:
. Найти:
1) длину отрезка  ;
;
2) уравнения прямых  и
и 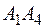 ;
;
3) угол между прямыми  и
и 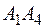 ;
;
4) уравнение плоскости 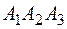 ;
;
5) угол между прямой 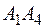 и плоскостью
и плоскостью 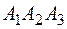 ;
;
6) уравнения высоты, опущенной из точки 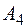 на плоскость
на плоскость  .
.
4. Найти пределы функций, не пользуясь правилом Лопиталя:
1)  ; 2)
; 2) 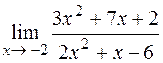 ; 3)
; 3) 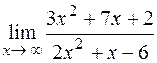 ;
;
4) 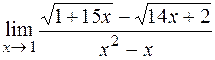 ; 5)
; 5) 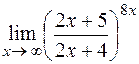 .
.
5. Дана функция 
Найти точки разрыва функции, если они существуют, и построить ее график.
ВАРИАНТ 3
Контрольная работа №1
1. Дана матрица 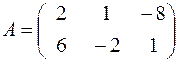 . Найти
. Найти 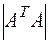 .
.
2. Решить систему линейных уравнений 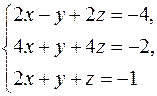
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
3. Дано:  ,
, 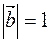 ,
, 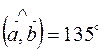 , векторы
, векторы  и
и 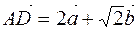 составляют стороны параллелограмма
составляют стороны параллелограмма  .
.
Найти:
1) длины диагоналей параллелограмма  ;
;
2) острый угол между диагоналями параллелограмма 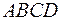 ;
;
3) площадь параллелограмма 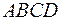 .
.
4. Даны точки  ;
; 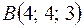 ;
; 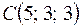 ;
;  . Требуется:
. Требуется:
1) записать векторы  ,
, 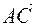 ,
, 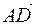 в ортонормированном базисе;
в ортонормированном базисе;
2) найти длины векторов 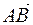 ,
, 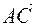 ,
, 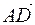 ;
;
3) показать, что векторы  ,
, 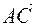 ,
,  образуют базис трехмерного пространства;
образуют базис трехмерного пространства;
4) найти острый угол между векторами 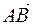 и
и 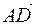 ;
;
5) найти алгебраическую проекцию вектора 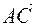 на вектор
на вектор 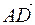 ;
;
6) найти площадь треугольника 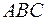 ;
;
7) найти объем пирамиды 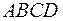 .
.
5. Найти собственные значения и собственные векторы матрицы 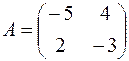 .
.
Контрольная работа №2
1. Даны координаты вершин треугольника 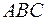 :
: 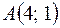 ,
,  ,
, 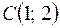 . Найти:
. Найти:
1) длину стороны  ;
;
2) уравнения сторон 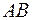 и
и 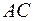 и их угловые коэффициенты;
и их угловые коэффициенты;
3) внутренний угол 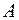 в радианах с точностью до
в радианах с точностью до 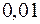 ;
;
4) уравнение высоты  и ее длину, не используя координаты точки
и ее длину, не используя координаты точки 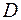 ;
;
5) уравнение медианы 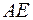 ;
;
6) точку пересечения высот треугольника 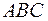 .
.
Сделать чертеж.
2. Составить уравнения прямых, проходящих через точку 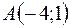 параллельно асимптотам гиперболы
параллельно асимптотам гиперболы 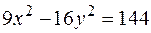 .
.
3. Даны точки 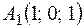 ;
;  ;
; 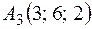 ;
; 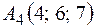 . Найти:
. Найти:
1) длину отрезка  ;
;
2) уравнения прямых  и
и 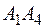 ;
;
3) угол между прямыми  и
и 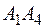 ;
;
4) уравнение плоскости 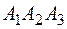 ;
;
5) угол между прямой  и плоскостью
и плоскостью 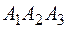 ;
;
6) уравнения высоты, опущенной из точки  на плоскость
на плоскость  .
.
4. Найти пределы функций, не пользуясь правилом Лопиталя:
1)  ; 2)
; 2) 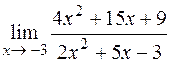 ; 3)
; 3) 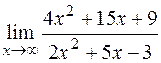 ;
;
4)  ; 5)
; 5) 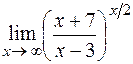 .
.
5. Дана функция 
Найти точки разрыва функции, если они существуют, и построить ее график.
ВАРИАНТ 4
Контрольная работа №1
1. Дана матрица  . Найти
. Найти 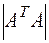 .
.
2. Решить систему линейных уравнений 
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
3. Дано:  ,
, 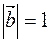 ,
, 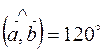 , векторы
, векторы  и
и  составляют стороны параллелограмма
составляют стороны параллелограмма  .
.
Найти:
1) длины диагоналей параллелограмма 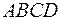 ;
;
2) острый угол между диагоналями параллелограмма  ;
;
3) площадь параллелограмма  .
.
4. Даны точки 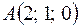 ;
; 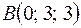 ;
; 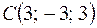 ;
; 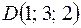 . Требуется:
. Требуется:
1) записать векторы  ,
, 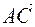 ,
, 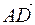 в ортонормированном базисе;
в ортонормированном базисе;
2) найти длины векторов 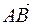 ,
, 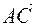 ,
, 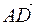 ;
;
3) показать, что векторы 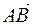 ,
,  ,
, 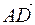 образуют базис трехмерного пространства;
образуют базис трехмерного пространства;
4) найти острый угол между векторами  и
и 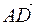 ;
;
5) найти алгебраическую проекцию вектора  на вектор
на вектор 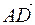 ;
;
6) найти площадь треугольника 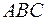 ;
;
7) найти объем пирамиды  .
.
5. Найти собственные значения и собственные векторы матрицы  .
.
Контрольная работа №2
1. Даны координаты вершин треугольника 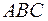 :
: 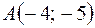 ,
, 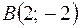 ,
,  . Найти:
. Найти:
1) длину стороны  ;
;
2) уравнения сторон  и
и 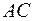 и их угловые коэффициенты;
и их угловые коэффициенты;
3) внутренний угол  в радианах с точностью до
в радианах с точностью до 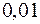 ;
;
4) уравнение высоты 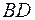 и ее длину, не используя координаты точки
и ее длину, не используя координаты точки  ;
;
5) уравнение медианы 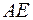 ;
;
6) точку пересечения высот треугольника 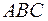 .
.
Сделать чертеж.
2. Дана парабола 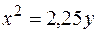 . Найти длину ее хорды, проходящей через точку
. Найти длину ее хорды, проходящей через точку 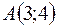 параллельно прямой
параллельно прямой 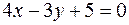 .
.
3. Даны точки 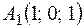 ;
; 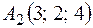 ;
; 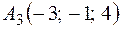 ;
;  . Найти:
. Найти:
1) длину отрезка  ;
;
2) уравнения прямых  и
и 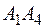 ;
;
3) угол между прямыми 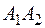 и
и  ;
;
4) уравнение плоскости  ;
;
5) угол между прямой  и плоскостью
и плоскостью  ;
;
6) уравнения высоты, опущенной из точки  на плоскость
на плоскость 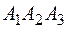 .
.
4. Найти пределы функций, не пользуясь правилом Лопиталя:
1) 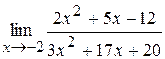 ; 2)
; 2)  ; 3)
; 3) 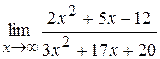 ;
;
4) 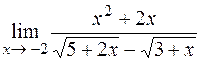 ; 5)
; 5)  .
.
5. Дана функция 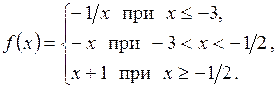
Найти точки разрыва функции, если они существуют, и построить ее график.
ВАРИАНТ 5
Контрольная работа №1
1. Дана матрица 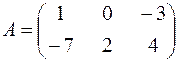 . Найти
. Найти 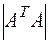 .
.
2. Решить систему линейных уравнений 
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
3. Дано: 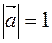 ,
, 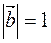 ,
,  , векторы
, векторы 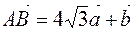 и
и 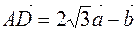 составляют стороны параллелограмма
составляют стороны параллелограмма  .
.
Найти:
1) длины диагоналей параллелограмма 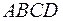 ;
;
2) острый угол между диагоналями параллелограмма 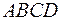 ;
;
3) площадь параллелограмма  .
.
4. Даны точки 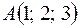 ;
;  ;
;  ;
;  . Требуется:
. Требуется:
1) записать векторы 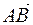 ,
, 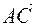 ,
, 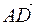 в ортонормированном базисе;
в ортонормированном базисе;
2) найти длины векторов  ,
, 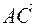 ,
,  ;
;
3) показать, что векторы 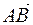 ,
, 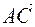 ,
, 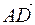 образуют базис трехмерного пространства;
образуют базис трехмерного пространства;
4) найти острый угол между векторами  и
и 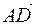 ;
;
5) найти алгебраическую проекцию вектора  на вектор
на вектор 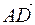 ;
;
6) найти площадь треугольника  ;
;
7) найти объем пирамиды  .
.
5. Найти собственные значения и собственные векторы матрицы 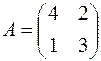 .
.
Контрольная работа №2
1. Даны координаты вершин треугольника  :
:  ,
, 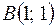 ,
,  . Найти:
. Найти:
1) длину стороны 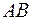 ;
;
2) уравнения сторон  и
и  и их угловые коэффициенты;
и их угловые коэффициенты;
3) внутренний угол 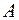 в радианах с точностью до
в радианах с точностью до 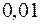 ;
;
4) уравнение высоты 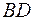 и ее длину, не используя координаты точки
и ее длину, не используя координаты точки 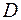 ;
;
5) уравнение медианы 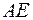 ;
;
6) точку пересечения высот треугольника 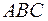 .
.
Сделать чертеж.
2. Составить уравнение прямой, проходящей через центр гиперболы  параллельно прямой
параллельно прямой 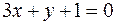 .
.
3. Даны точки 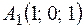 ;
;  ;
;  ;
;  . Найти:
. Найти:
1) длину отрезка 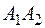 ;
;
2) уравнения прямых  и
и  ;
;
3) угол между прямыми 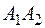 и
и  ;
;
4) уравнение плоскости 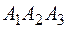 ;
;
5) угол между прямой  и плоскостью
и плоскостью 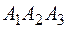 ;
;
6) уравнения высоты, опущенной из точки  на плоскость
на плоскость 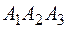 .
.
4. Найти пределы функций, не пользуясь правилом Лопиталя:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 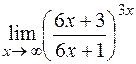 .
.
5. Дана функция 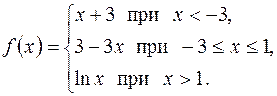
Найти точки разрыва функции, если они существуют, и построить ее график.
ВАРИАНТ 6
Контрольная работа №1
1. Дана матрица 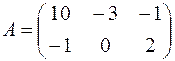 . Найти
. Найти 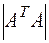 .
.
2. Решить систему линейных уравнений 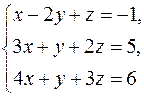
1) по правилу Крамера;
2) с помощью обратной матрицы;
3) методом Гаусса.
3. Дано: 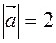 ,
, 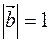 ,
,  , векторы
, векторы 