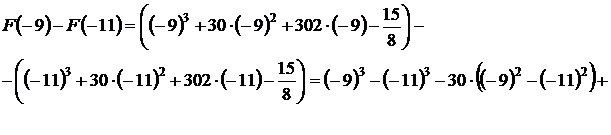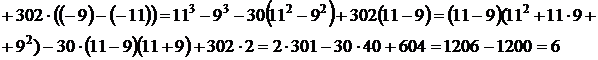РЕШЕНИЕ. ПРОФИЛЬНЫЙ УРОВЕНЬ.
ВАРИАНТ 1
Задание 1 № 501592
Павел Иванович купил американский автомобиль, на спидометре которого скорость измеряется в милях в час. Американская миля равна 1609м. Какова скорость автомобиля в километрах в час, если спидометр показывает 50 миль в час? Ответ округлите до целого числа.
Решение
Поскольку 1 миля равна 1609 м, 50 миль/ч составляют 50·1609м/ч = 80450 м/ч = 80,45 км/ч. Округляя найденную величину, получаем 80.
Ответ: 80.
Примечание.
Округлять следует сразу до нужного количества знаков, а не поэтапно. Поэтому 80,45 округляется до 80, а не до 81, как можно было бы подумать, сначала округлив до 80,5, а потом до 81.
Задание 2 № 525715
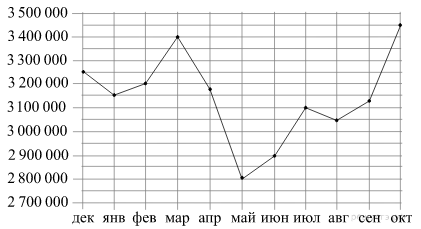
На рисунке точками показана месячная аудитория поискового сайта f4h0.ru во все месяцы с декабря 2008 года по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали – количество человек, посетивших сайт хотя бы раз за данный месяц. Для наглядности точки на рисунке соединены линией. Определите по рисунку наименьшую месячную аудиторию сайта f4h0.ru в период с декабря 2008 года по апрель 2009 года.
Решение
Из рисунка видно, что наименьшая месячная аудитория в период с декабря 2008 года по апрель 2009 года была равна 3 150 000 в январе.
Ответ: 3 150 000.
Задание 3 № 27701
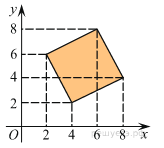Найдите площадь четырехугольника, вершины которого имеют координаты (4; 2), (8; 4), (6; 8), (2; 6).
Решение
Четырехугольник является квадратом. Площадь квадрата равна квадрату его стороны. Сторона квадрата равна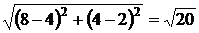 
, тогда площадь квадрата S = 20.
Ответ: 20.
Задание 4 № 320176
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
|
|
Решение
Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P (A + B + С) = P (A) + P (B) + P (С)= P (A) + P (B),
откуда, используя данные из условия, получаем
0,97 = P (A) + 0,89.
Тем самым, для искомой вероятности имеем:
P (A) = 0,97 − 0,89 = 0,08.
Ответ: 0,08.
Задание 5 № 501205
Решите уравнение: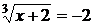 
.
Решение
Возведем обе части уравнения в третью степень:
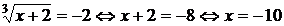
Ответ: –10.
Задание 6 № 27934
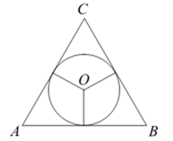
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Решение
Радиус вписанной окружности равен отношению площади к полупериметру. Для нахождения площади, воспользуемся формулой Герона:
.
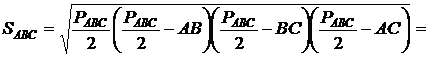
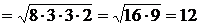Тогда
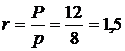
Ответ: 1,5.
Задание 7 № 323079
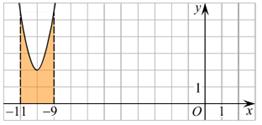На рисунке изображён график функции y = f (x).
Функция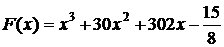 
– одна из первообразных функции y = f (x). Найдите площадь закрашенной фигуры.
Решение
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках –9 и –11.
Имеем:
.
.
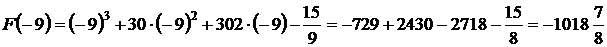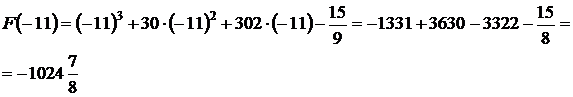
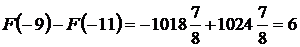Приведем другое решение.
Вычисления можно было бы упростить, выделив полный куб:
,
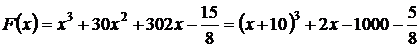что позволяет срезу же найти
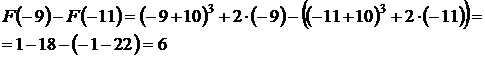
Приведем ещё одно решение.
Можно было бы найти разность первообразных, используя формулы сокращенного умножения:
|
|
