Основные понятия и формулы
Комплексными числами называются упорядоченные пары 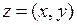 действительных чисел, для которых следующим образом определены операции сложения и умножения: если
действительных чисел, для которых следующим образом определены операции сложения и умножения: если 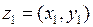 и
и  , то
, то
 ,
,  .
.
 Комплексное число изображается точкой или вектором на координатной плоскости (рис. 1.1). Множество всех комплексных чисел обозначается буквой
Комплексное число изображается точкой или вектором на координатной плоскости (рис. 1.1). Множество всех комплексных чисел обозначается буквой 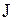 . Действительные числа
. Действительные числа  и
и  называются действительной и мнимой частью комплексного числа
называются действительной и мнимой частью комплексного числа 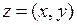 . Если
. Если  ,
,  то
то  ;
;  . Поэтому комплексное число вида
. Поэтому комплексное число вида  естественно отождествить с действительным числом
естественно отождествить с действительным числом 
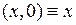 .
.
Все свойства сложения и умножения действительных чисел переносятся и на комплексные числа.
Число 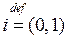 называется мнимой единицей; его квадрат:
называется мнимой единицей; его квадрат:
 .
.
Каждое комплексное число 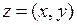 можно представить в виде
можно представить в виде  или, используя введенные выше отождествления, в виде
или, используя введенные выше отождествления, в виде  или
или  . В дальнейшем будем пользоваться именно такой записью комплексных чисел. Она удобна тем, что числа
. В дальнейшем будем пользоваться именно такой записью комплексных чисел. Она удобна тем, что числа  и
и  можно складывать и умножать по «обычным» правилам как двучлены, не обращаясь к определению этих действий:
можно складывать и умножать по «обычным» правилам как двучлены, не обращаясь к определению этих действий:
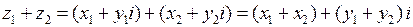 ,
,

Модулем комплексного числа  называется число
называется число
 ,
,
а аргументом любое число 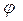 такое, что
такое, что
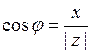 ,
,  . (1.1)
. (1.1)
Геометрический смысл чисел  и
и  изображен на рис. 1.1. Аргумент определен с точностью до слагаемого
изображен на рис. 1.1. Аргумент определен с точностью до слагаемого  ,
,  . То единственное значение аргумента, которое удовлетворяет неравенству
. То единственное значение аргумента, которое удовлетворяет неравенству  , называется его главным значением и обозначается
, называется его главным значением и обозначается  .
.
Из (1.1) получаем тригонометрическую форму комплексного числа
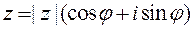 . (1.2)
. (1.2)
Обозначив здесь  , получим показательную форму комплексного числа
, получим показательную форму комплексного числа
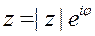 . (1.3)
. (1.3)
Для возведения числа z в степень  удобно записать его в показательной форме (1.2) и воспользоваться формулой Муавра
удобно записать его в показательной форме (1.2) и воспользоваться формулой Муавра
 . (1.4)
. (1.4)
Корнем n-ной степени из комплексного числа  называется любое такое комплексное число w, что
называется любое такое комплексное число w, что  . Существует ровно n различных значений корня из комплексного числа
. Существует ровно n различных значений корня из комплексного числа 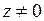 ; все они обозначаются
; все они обозначаются  ,
, 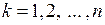 и находятся по формуле
и находятся по формуле
 ,
,  ;
; 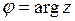 . (1.5)
. (1.5)
Здесь  – действительное положительное число.
– действительное положительное число.
Число  называется комплексно-сопряженным числу
называется комплексно-сопряженным числу  (см. рис 1.1). Операция сопряжения имеет следующие свойства:
(см. рис 1.1). Операция сопряжения имеет следующие свойства:
1) 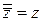 ;
;
2)  ;
;
3) 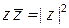 ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ,
,  ;
;
7) Если  , то
, то 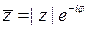 .
.
Примеры решения задач
1.2.1. Найти  , если
, если  .
.
◀  ;
;
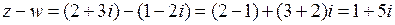 ;
;
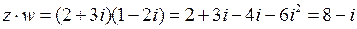 (здесь учтено, что
(здесь учтено, что  );
);
 ,
,  (здесь учтено, что
(здесь учтено, что  ).
).


 ▶
▶
1.2.2. Записать комплексное число  в тригонометрической и показательной формах.
в тригонометрической и показательной формах.
◀ Модуль числа  . Главное значение аргумента
. Главное значение аргумента 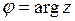 найдем из условий (1.1):
найдем из условий (1.1):  ;
;  . Следовательно,
. Следовательно,  . По формулам (1.2) и (1.3) получаем тригонометрическую и показательную форму числа:
. По формулам (1.2) и (1.3) получаем тригонометрическую и показательную форму числа:  и
и  ▶
▶
1.2.3. Найти  .
.
◀ Комплексное число  представим в показательной форме:
представим в показательной форме:  ; так как
; так как  и
и 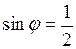 , то
, то  , и поэтому
, и поэтому
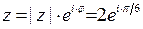 .
.
Теперь по формуле Муавра (1.4)
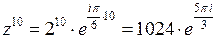 .
.
 Перейдя к тригонометрической форме, получим
Перейдя к тригонометрической форме, получим
 ▶
▶
1.2.4. Найти все значения  .
.
◄ Так как 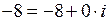 , то модуль этого числа
, то модуль этого числа  , а аргумент
, а аргумент  находим из условий
находим из условий 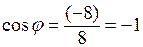 ,
, 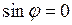 ;
;  , откуда
, откуда  (рис. 1.2). По формуле (1.5) имеем далее
(рис. 1.2). По формуле (1.5) имеем далее
 ,
,  .
.
При 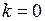
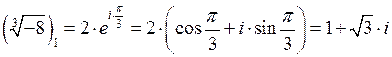 ,
,
при 
 ,
,
при 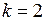
 . ▶
. ▶
1.2.5. Описать геометрически следующие множества:

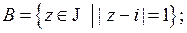
 ;
;  .
.
◄ Поскольку  , то множество A представляет собой полосу между горизонтальными прямыми
, то множество A представляет собой полосу между горизонтальными прямыми 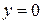 и
и  (рис. 1.3).
(рис. 1.3).
Модуль разности  между двумя комплексными числами является расстоянием между изображающими их точками на плоскости, поэтому B представляет собой окружность радиуса 1 с центром в точке
между двумя комплексными числами является расстоянием между изображающими их точками на плоскости, поэтому B представляет собой окружность радиуса 1 с центром в точке  .
.

 Множество C изображено на рис. 1.4. Неравенства
Множество C изображено на рис. 1.4. Неравенства  задают кольцо между двумя окружностями
задают кольцо между двумя окружностями 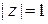 и
и  радиусов 1 и 2 с центрами в точке 0. Неравенства
радиусов 1 и 2 с центрами в точке 0. Неравенства  задают сектор между двумя лучами
задают сектор между двумя лучами 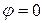 и
и  .
.
Так как  , то
, то  ; то есть множество D представляет собой внешность круга радиуса
; то есть множество D представляет собой внешность круга радиуса 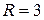 с центром в точке 0 (см. рис. 1.4). ▶
с центром в точке 0 (см. рис. 1.4). ▶
Задачи для самостоятельного решения
В задачах 1.3.1 и 1.3.2 изобразить на комплексной плоскости 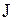 числа
числа  ,
, 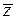 и
и  ; найти
; найти 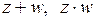 и
и  .
.
1.3.1.  , ,  . .
| 1.3.2. 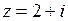 , ,  . .
| |
1.3.3.Вычислить  . .
| 1.3.4.Вычислить  . .
| |
1.3.5.Найти  . .
| 1.3.6.Найти  . .
| |
1.3.7.Найти все значения  . .
| 1.3.8.Найти все значения  . .
| |
В задачах 1.3.9 и 1.3.10 найти модуль и аргумент комплексного числа  , записать его в тригонометрической и показательной формах.
, записать его в тригонометрической и показательной формах.
1.3.9. 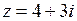 ; ;
| 1.3.10. 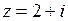 . .
|
В задачах 1.3.11 и 1.3.12 описать геометрически указанные множества.
1.3.11.  ; ;
 ; ;
 ; ;
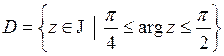 . .
| 1.3.12.  ; ;
 ; ;
 ; ;
 . .
|
1.3.13. Используя свойства операции сопряжения, найти выражение 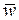 через
через  , если
, если  .
.
1.3.14. Используя свойства операции сопряжения, доказать, что число  является действительным при любом
является действительным при любом 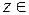
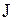 ,
, 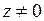 .
.